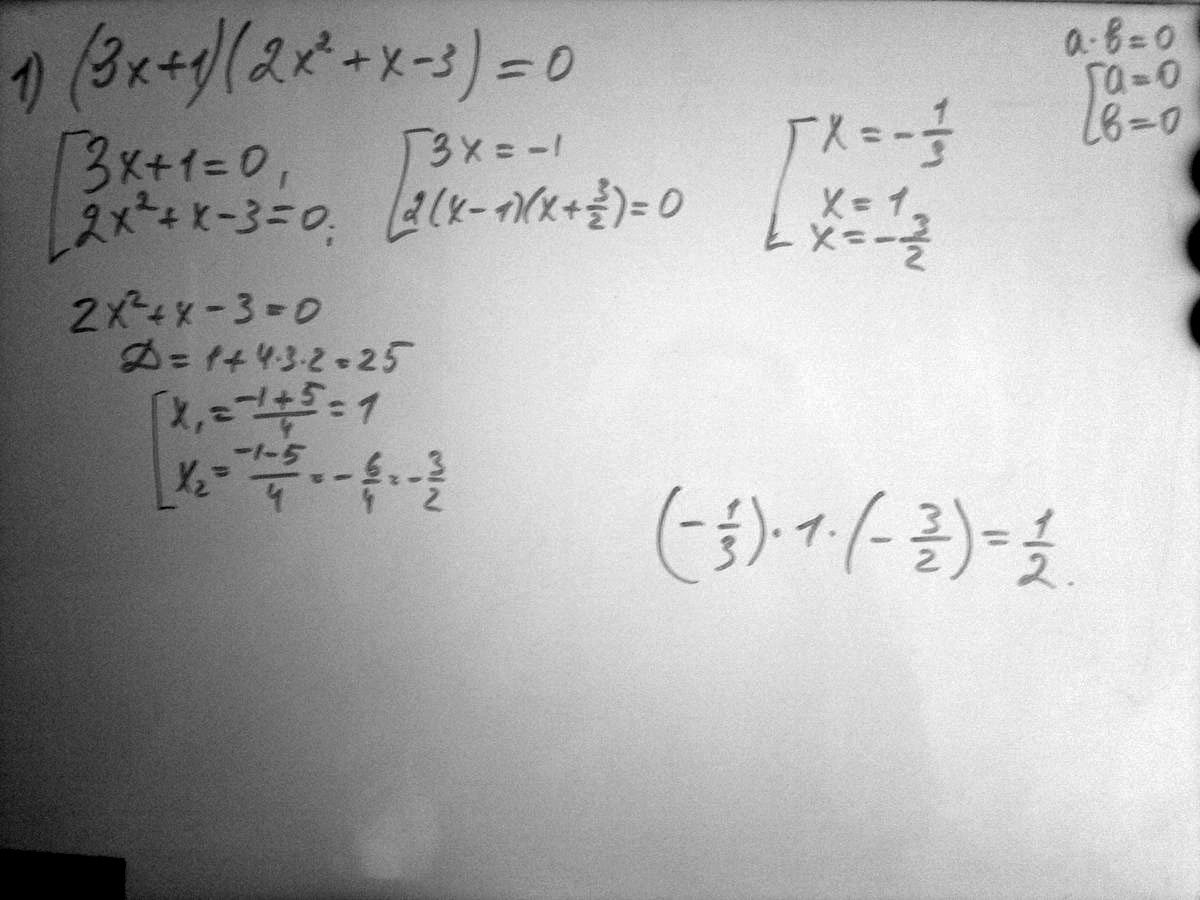решение уравнений »
сколько действительных корней имеет уравнение - страница 2
Сколько действительных корней имеет система x+ y=2 и xy-z^2=1
Решение: {x+y =2 ; xy -z² =1 ;
{x+y =2 ; xy =z² +1 ;
* * * x и y корни уравнения t² -2t +(z² +1) =0 (обратная теорема Виета) * * *
t² -2t +(z² +1) =0 ; * * * (t -1)² +z² =0 ⇔ z=0 ; t=1 * * *
D =1² -(z² +1) = - z² ≤0 . Имеет действительное решение, если z =
тогда t² -2t +1 =0 ⇔(t -1)² =0⇒t=1.
одно решение: x=y =1.Найдите произведение корней: (3х+1)(2х(квадрат)+х-3)=0 Сколько действительных корней имеет уравнение (3х-1)(2х(квадрат)+3х+2)=0
Сколько действительных корней имеет уравнение (2-3х(квадрат))(х(квадрат)-5х+3)=0
Решение: Решение на фото, которое прикреплено (3х+1)(2х^2+х-3)=0
3x+1=0
x=-1/3 2x^2+x-3=0 x1=1 x2=3/2
x*x1*x2= -1/3*1*3/2=-1/2
(2-3х^2)(х^2-5х+3)=0
2-3х^2=0 х^2-5х+3=0 D=25-12=13 D>0 2 корня
-3x^2=-2
x^2=2/3
x=+-2/3
ответ: 4 действительных корня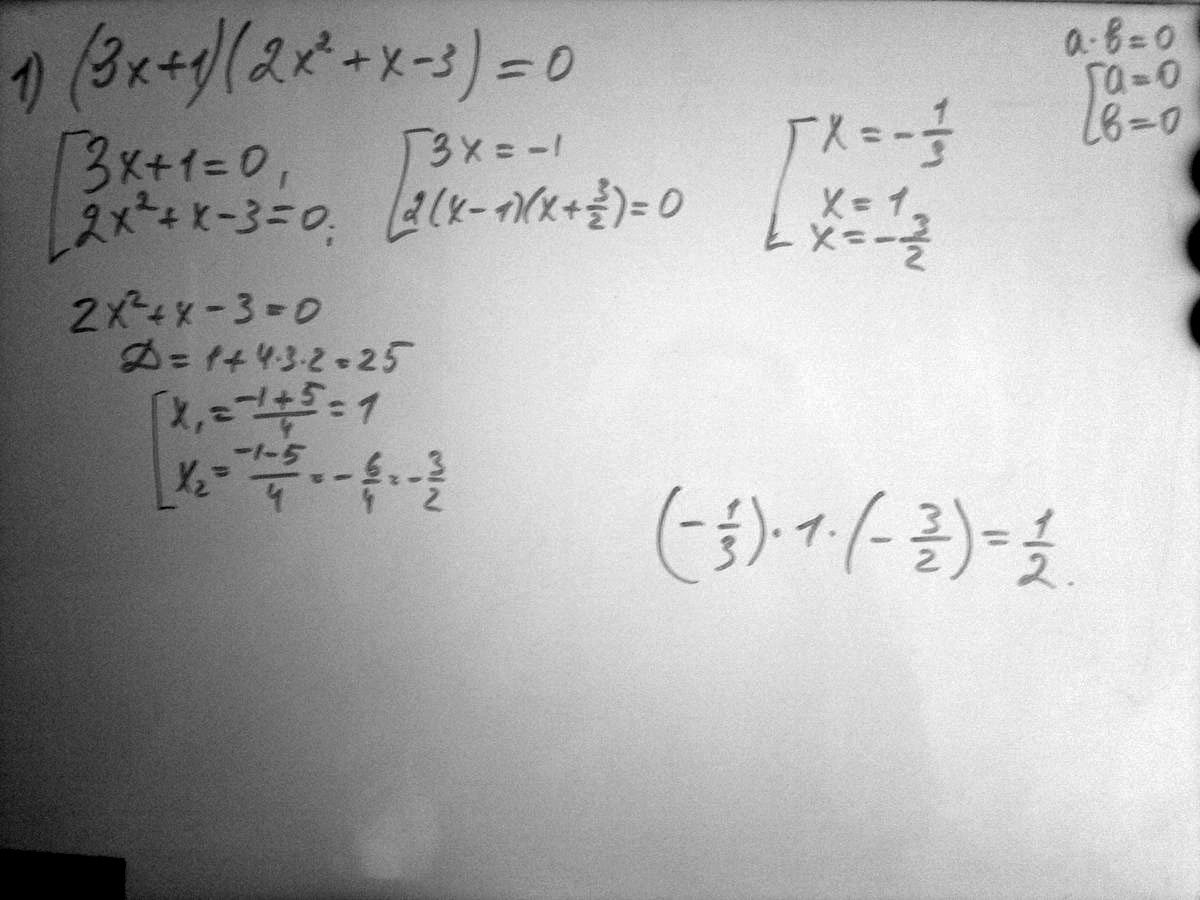
Сколько существует значений а, при которых уравнение "модуль(x^2-5*a*x)=15*a" имеет три различных действительных корня?
Решение: Итак, уравнение такое
|x^2 - 5ax| = 15a
Из уравнения сразу ясно, что a >= 0, потому что модуль >= 0.
1) При а = 0
|x^2 - 0| = 0; x = 0 - единственный корень, не подходит.
2) x^2 - 5ax = -15a < 0
x^2 - 5ax = x(x - 5a) < 0
a > 0, то есть 5a > 0, тогда 0 < x < 5a
|x^2 - 5ax| = 5ax - x^2
Подставляем
5ax - x^2 = -15a
5ax - x^2 + 15a = 0
x^2 - 5ax - 15a = 0
D = 25a^2 + 4*15a = 25a^2 + 60a > 0 при любом a > 0
x1 = (5a - √(25a^2 + 60a)) / 2; x2 = (5a + √(25a^2 + 60a)) / 2
3) 5ax - x^2 = 15a > 0
5ax - x^2 - 15a = 0
x^2 - 5ax + 15a = 0
D = 25a^2 - 4*15a = 25a^2 - 60a = 5a(5a - 12) > 0
5a(5a - 12) > 0, при этом мы знаем, что a > 0, тогда
5a - 12 > 0; a > 12/5
x1 = (5a - √(25a^2 - 60a)) / 2; x2 = (5a + √(25a^2 - 60a)) / 2
3) При а = 12/5 будет
|x^2 - 12x| = 15*12/5 = 3*12 = 36
a) x^2 - 12x = 36
x^2 - 12x - 36 = 0;
D/4 = 6^2 + 36 = 72 = (6√2)^2
x1 = 6 - 6√2; x2 = 6 + 6√2
b) x^2 - 12x = -36
x^2 - 12x + 36 = 0
(x - 6)^2 = 0
x3 = 6
При а = 12/5 будет 3 корня
Ответ: три корня будет только при а = 12/5
-х^2+11х-30<0. Можно ли найти через дискриминант, если А-отрицательный?
Решение: -х²+11х-30<0
а= -1 в= 11 с= -30
Д= в²-4ас=(-11)²-4·(-1)·(-30)=121-120=1>0⇒2 корня
-в +/-√Д -11+/-√1 -11+/-1
х=---------------= -------------- = -----------
2а 2·(-1) -2
-11+1 10
х₁= ------------- = -------------= -5
-2 -2
-11-1 -12
х₂= -----------= ----------- = 6
-2 -2
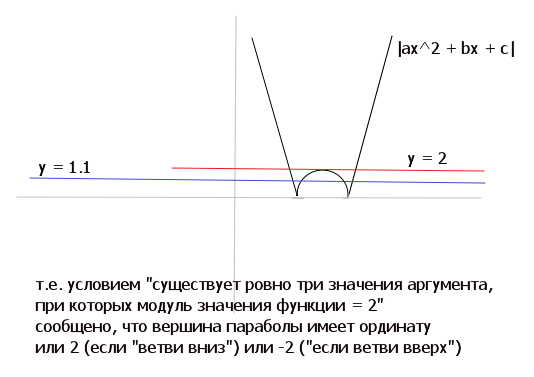
ответ: -5 и 6Про квадратичную функцию f известно, что существует ровно три значения аргумента, при которых модуль значения
функции равен 2. Сколько корней имеет уравнение f(x) = 1,1?
Решение: Ответ: ровно ДВА корня.
т. к. прямая у = 1.1 пересечется с графиком (параболой) в двух точках.
это будет или ниже или выше вершины)))
в зависимости от направления ветвей.