какое из уравнений не имеет корней
А. 50 1. Составьте числовое выражение и найдите его значение:
Произведение числа 100 и суммы чисел 15 и 17.
А. 320. Б. 32. В. 3200. Г. 32000.
2. Собственная скорость лодки равна х км/ч, а скорость течения реки равна 3 км/ч. Какое расстояние пройдет лодка за 2 ч, двигаясь против течения реки?
А. (х + 3) км. В. (х - 3) км.
Б. 2(х - 3) км. Г. 2(х + 3) км.
3. Найдите периметр прямоугольника АВСД со сторонами АВ=20 см, ВС= 30 см.
см. Б. 100 см. В. 10 см. Г. 200 см.
6. Найдите путь s, если v = 18 км/ч, t=0,5 ч.
А. 90 км. Б. 9 км. В. 36 км. Г. 360 км.
7. Решите уравнение 320 : х = 40
А. 80. Б. 280. В. 360. Г.
Решение: 1. 100*(15+17)=3200Ответ Г
2. s=v*t v=(x-3), t=2
2(х - 3)
Ответ: Б
3. 20+20+30+30=100
Ответ: Б
6.s=v*t
s=18*0,5=9 км
Ответ: Б
7.320 : х = 40
x=320:40
x=8
Ответ Г
1) Какое из следующих чисел является наименьшим?
а) 6,2*10^(-3) (умножить на 10 в минус третьей степени)
б) 5,3*10^(-4)
в) 7,2*10^(-3)
г) 5.9*10(-4)
2)Найдите значение выражения:
√720*√120/√40
3) Решите уравнение:
(x-1)^2 = (11-x)^2
Решение: 1) Ответ: б
а) = 6,2*0,001 = 0,0062
б) = 5,3*0,0001 = 0,00053
в) = 7,2*0,001 = 0,0072
г) = 5,9*0,0001 = 0,00059
2) ответ: 60√6 / √10
√720*√120 / √40 = √4*4*9*5 * √4*30 / √4*10 = 2*2*3√5 * 2√30 / 2√10 = 12√5*√30 / √10 = 12√150 / √10 = 12*√25*6 / √10 = 12*5√6 / √10 = 60√6 / √10
3) ответ: х=6
х²-2х+1=121-22х+х²
-2х+22х=121-1
20х=120
х=120/20
х=6
проверка:
(6-1)²=(11-6)²
5²=5²
25=25
При каких значениях р произведение корней квадратного уравнения х^2+3х+(р^2-7р+12)=0 равнонулю
Решение: Произведение корней квадратного уравнения равно нулю тогда, когда свободный член равен нулю ( он отсутствует ), т.к. по теореме Виета x1*x2=c/a.
В данном уравнении роль свободного члена выполняет выражение p^2-7p+12. Приравняем его к нулю:
p^2-7p+12=0
D=(-7)^2-4*12=1
p1=(7-1)/2=3
p2= (7+1)/2=4
Ответ: p1=3; p2=4При каких значениях а один из корней уравнения \( x^{2} -2(a+1)x+4a+1=0 \) меньше 1, а другой- больше 1?
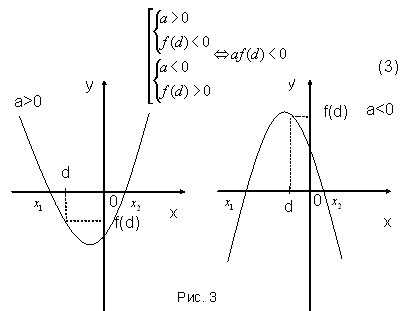
Решение: Для того, чтобы число d было расположено между корнями квадратного трёхчлена, необходимо и достаточно выполнение условий на рисунке (). Так как у нас коэффициент при x^2 положителен и равен 1, то достаточно выполнение условия f(x) < 0. Решаем:
$$ 1^2-2(a+1)*1+4a+1<0 \\ 1-2a-2+4a+1<0 \\ 2a<0 \\ a<0 $$
1)D>0⇒4(a+1)²-4(4a+1)=4a²+8a+4-16a-4=4a²-8a=4a(a-2)>0
a=0 a=2
+ _ +
_________________________
0 2
a<0, a>2
2) Т.к.a>0⇒f(x)<0
1-2(a+1)+4+1<0
1-2a-2+4a+1<0
2a<0
a<0
Общее a<0⇒a∈(-∞;0)
a>2
При каких значениях а один из корней уравнения (2а+1)х^2-ах+а-2=о меньше1,а другой больше1?
Решение: 1) При 2a+1>0 парабола с ветвями вверх. То есть a > -1/2. Так как один из корней больше 1, а другой меньше 1, то значение функции в точке x=1 должно быть меньше 0. То есть (2a+1)*1^2-a*1+a-2=2a-1<0 => a < 1/2.
То есть -1/2<a<1/2
2) При 2a+1<0 парабола с ветвями вниз. То есть a < -1/2. Так как один из корней больше 1, а другой меньше 1, то значение функции в точке x=1 должно быть больше 0. То есть 2a-1>0 => a > 1/2. Решений в этом случае нет.
Таким образом, a∈(-1/2;1/2)1. разложите число 56 на три множителя двумя способами
2. Один спортсмен пробежал дистанцию в 54 км за 6 часов, а другой дистанцию 72 км за 9 часов. У кого из них скорость больше?3. Найдите куб и квадрат числа 13.
4. Решите уравнение 75*у=900
5. Скорость поезда 68 км/ч, а скорость автомобиля на 24 км/ч больше. Какое расстояние может преодалень каждый из этих видов транспорта за 3 ч?
6. Выполните действия:216*24-121*31+27*51
7. Найдите значения выражения:342+45*х, если х=403.
8. Выполните деление с остатком:34895 на 174.
Решение: 1. 14*1*4 7*4*2
2. Скорость первого - 54/6 = 9км/ч. Скорость второго - 72/9 = 8 км/ч. Соответственно у первого.
3. 13^3 (13*13*13) = 2197 13^2 (13*13) = 169
4. 75y=900
y=900/75
y=12
5. Поезд за 3ч преодолеет 68*3=204 (км)
Машина - 24*3=72 (км)
6. 216*24 - 121*31 + 27*51 = 5184 - 3751 + 1377 = 2810
7. Если х=403, то 342+45х = 342+45*403 = 342 + 18135 = 18477
8.34895/174=200 с остатком 95.
