неравенства »
решите неравенство графически - страница 2
Решите графически неравенство: а) (x+1)^2 больше 4
б) x^2 - 2x меньше 3
Решение: (x+1)^2>4 => (x+1)^2-4>0 график - парабола, сдвинутая на 1 влево по оси х и опущена на 4 вниз по у, вершина -(-1,- 4) ответ (от - беск. до -3 и 1 до +беск)
x^2-2x-3<0 квадратный трехчлен , найдем 0 - x^2-2x-3=0 d=4+4*3=16 vd=4
x1=2-4/2=-1 x2=2+4/2=3 ответ от -1 до 3
нули ф-ции (x+1)^2-4=0 x1=-3 x2=1Решите графически неравенство:x^2-1 больше или равно нулю.
Решение: По формуле разности квадратов левая часть неравенства раскладывается на множители
х²-1=(x-1)(x+1)
Неравенство принимает вид
(x-1)(x+1)≥0
Решаем методом интервалов, отмечаем корни уравнения (x-1)(x+1)=0, точки х=-1 и х=1 на числовой прямой и отмечаем знаки:
+ - +
------------[-1]-------------[1]------
Ответ (-∞;-1] U [1;+∞)Решите графически неравенство: х^2<2+х
Решение: Рисуем графики х^2 и 2+х
Раз 2+х больше то берется зона графика х^2 ниже этого графика.
Ответ:(-1;2) подробнее в графике(вложение)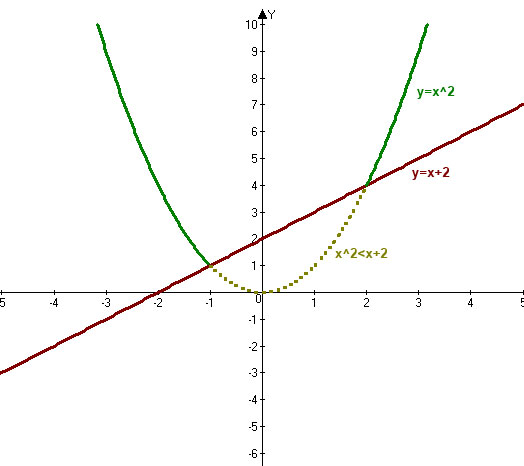
Решите графически неравенство: $$ x^2 \ge 6 - x \\ x^2 \le -x + 2 $$
Решение: Приравнивая левые и правые части неравенств, находим точки пересечения графиков левой и правой части ( эти точки указаны на рисунках). При значениях $$ x \leq - 3 $$ и $$ x \geq 2 $$ график параболы, то есть левой части неравенства находиться выше прямой которая есть график правой части. Эти значения и будут графическим решением первого неравенства, второе неравенство решается абсолютно аналогично, только точки пересечения графиков левой и правой части 1 и -2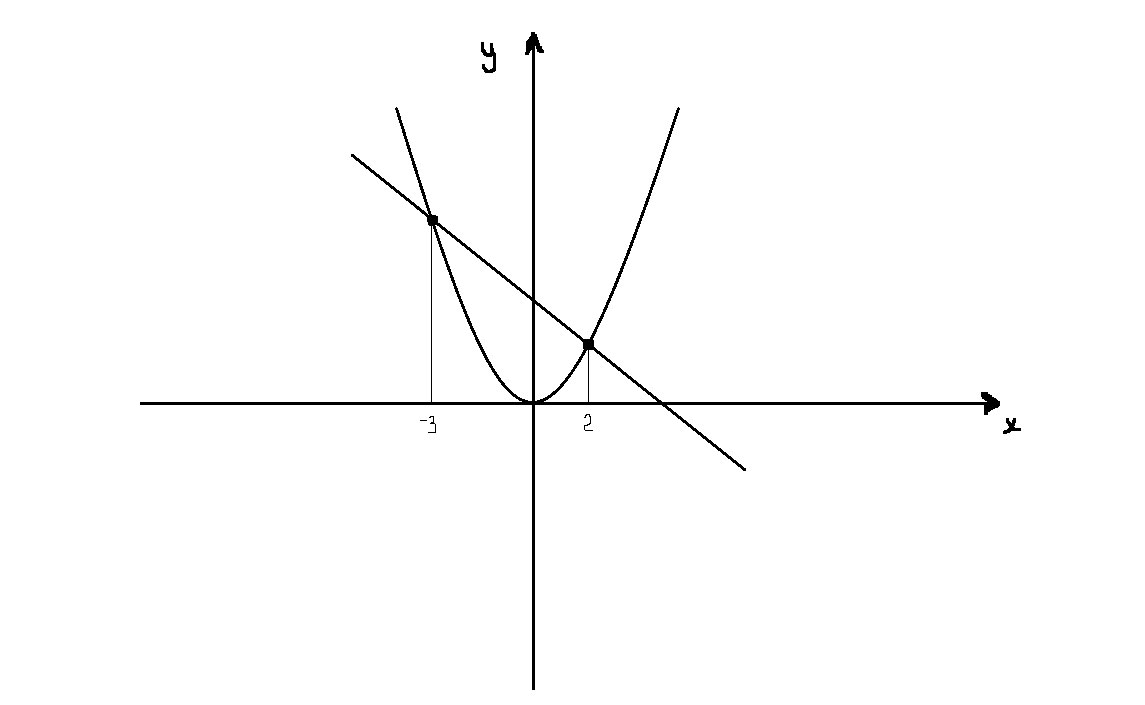
Найдите графическое решение неравенства х^2-х-6 <0
Решение: х²-х-6 <0
1. Найдём корни
х²-х-6 =0
D=b²-4ac=(-1)²-4*1*(-6)=1+24=25
x₁=(-b+√D)/2a=(-(-1)+5)/2*1=(1+5)/2=3
x₂=(-b-√D)/2a=(-(-1)-5)/2*1=(1-5)/2=-2
или
х²-х-6 =0
х₁*х₂=-6
х₁+х₂=1
х₁=3
х₂=-2
2. Построим график (см. во вложении):
1) Ветви параболы направлены вверх
Парабола проходит через точки 3 и -2
Ответ: (-2;3)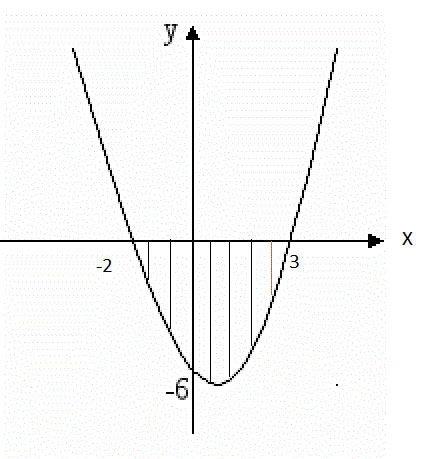




 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...