неравенства »

решите неравенство со степенями

  • Решите неравенство \(x^{4}\leq 625 \)


    Решение:

    $$ x^{4}\leq 625 $$

    $$ x^{4}-625\leq0 $$

    $$ (x^{2}-25)(x^{2}+25)\leq0 $$

    $$ x^{2}+25>0 $$ для любого х

    $$ x^{2}-25\leq0 $$

    $$ (x-5)(x+5)\leq0 $$

            +                _                    +

    ____________ -5 ___________ 5 __________

    Ответ: [-5;5]

  • Решить уравнение, 9 класс \( \sqrt{x + 17} - \sqrt{x + 1} = 2 \). Тема: неравенства, содержащие степень.


    Решение: √(x+17) - √(x+1) =2
    ОДЗ: x+17≥0 x+1≥0
      x≥ -17 x≥ -1
    x∈[-1; +∞)

    (√(x+17) - √(x+1))² = 2²
    x+17 - 2√[(x+17)(x+1)]+x+1 =4
    2x+18 - 2√(x²+17x+x+17) =4
    -2√(x²+18x+17)= -2x+4-18
    -2√(x²+18x+17)= -2x -14
    √(x²+18x+17) = x+7
    x²+18x+17=(x+7)²
    x²+18x+17=x²+14x+49
    x²-x²+18x-14x=49-17
    4x=32
    x= 8
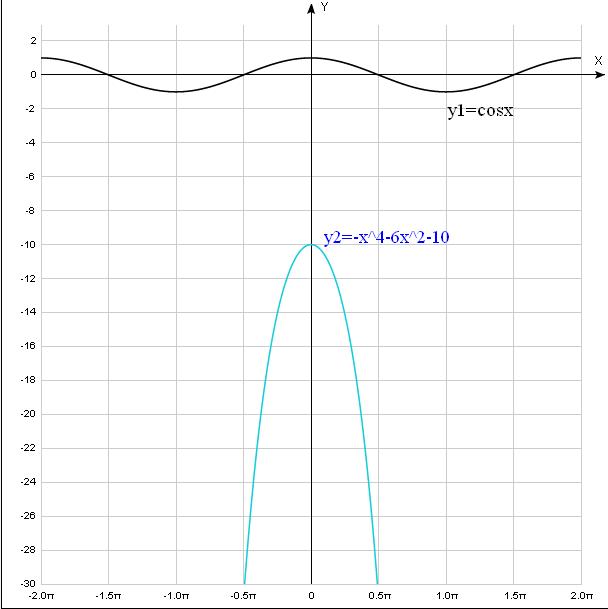
    Ответ: 8

  • Решить неравенство \( 3-cosx \leq x^{4}+6x^{2}+13 \)


    Решение: $$ 3-cosx \leq x^{4}+6x^{2}+13 $$
    $$ -cosx \leq x^{4}+6x^{2}+13-3 $$
    $$ cosx \geq -x^{4}-6x^{2}-10 $$

    Решим графически:
    $$ y_{1}(x)=cosx $$
    $$ y_{2}(x)=-x^{4}-6x^{2}-10 $$
    Функция косинуса - известная функция.
    Для построения функции $$ y_{2}(x)=-x^{4}-6x^{2}-10 $$:
    1) Нули функции: $$ -x^{4}-6x^{2}-10=0 $$
    $$ t^{2}+6t+10=0, D=36-40<0 $$ - график не пересекает ось Ох.
    2) $$ y_{2}(0)=-10 $$
    3) Точки максимума и минимума:
    \( y_{2}’(x)=-4x^{3}-12x=-4x*(x^{2}+3)=0 \)
    x=0 - при переходе через эту точку производная меняет свой знак с плюса на минус, значит это точка максимума
    4) Функция возрастает при x<0, убывает при x>0.

    По рисунку видно, что график функции \( y_{1}(x)=cosx \) всегда ВЫШЕ графика функции \( y_{2}(x)=-x^{4}-6x^{2}-10 \).

    Ответ: х - любое число (x∈R)

    -cosx leq x x -cosx leq x x - cosx geq -x - x - Решим графически y x cosx y x -x - x - Функция косинуса - известная функция.Для построения функции  y x -x - x - Нули функци...

  • Решить неравенство 9^х≥(1/27)^2-х9 в степени х больше или равно одной целой 27 сотых в степени 2 минус х


    Решение: $$ 3^{2x} \geq (3^{-3})^{2-x} \\ \ 3^{2x} - 3^{-3 \cdot (2-x)} \geq 0 \\ \ 3^{2x} - 3^{3x-6} \geq 0 \\ \ 3^{2x}-\frac{3^{3x}}{3^6} \geq 0 \\ \ t=3^{x} \\ (t > 0) \\ \ t^2 -\frac{t^3}{3^6} \geq 0 \\ \ 3^6 \cdot t^2 -t^3 \geq 0; \\ \ \\ -t^2 \cdot (t-3^6) \geq 0; \\ \ \\ t^2 \cdot (t-3^6) \leq 0 \\ \ t^2 \cdot (t-3^6)= 0 \\ t^2=0; \\ t=0 \\ (t > 0) ; \\ \ \\ \ \\ t=3^6 \\ \ 3^x=3^6 \\ \ \boxed{x=6} $$

       - +
    --------------*----------------->x
       6

    $$ x \leq 6 $$

  • Решите пожалйста. Системы Неравенств 1 степени 1) 58x-39 < 35x+44 36x+23 < 29x+37 2) 26x-37 <15x+18
    14x+63 < 31x+52 Отсутсовал 2 недели в школе,понятия не имею как решать...


    Решение: решается  как уравнение,переносится всё в 1 сторону

    1)58х-39-35x-44<0

    23x-83<0

    23x<83

    x<3,6

    1) 58x-39 < 35x+44

        58х-39-35х-44<0

        23x-83<0

        23x<83

        x< 3,6

        36x+23 < 29x+37

        36x+23-29x-37<0

         7x-14<0

          x<2

        

    2) 26x-37 < 15x+18

        26x -37-25x-18<0

        1x-55<0

         x<55
        14x+63 < 31x+52

        14x+63-31x-52<0

        11-7x<0

        7x<11

         x<1,57