неравенства »
найдите решение неравенства - страница 2
Найдите решение неравенства: а) 89/90 меньше x меньше 1 б) 3/7 меньше x меньше 4/7
в) 1/5 меньше x меньше 1/4
Решение: Принцип задания простой
главное знать какое число больше а какое меньше чтобы правильно расположить их в двойном неравенстве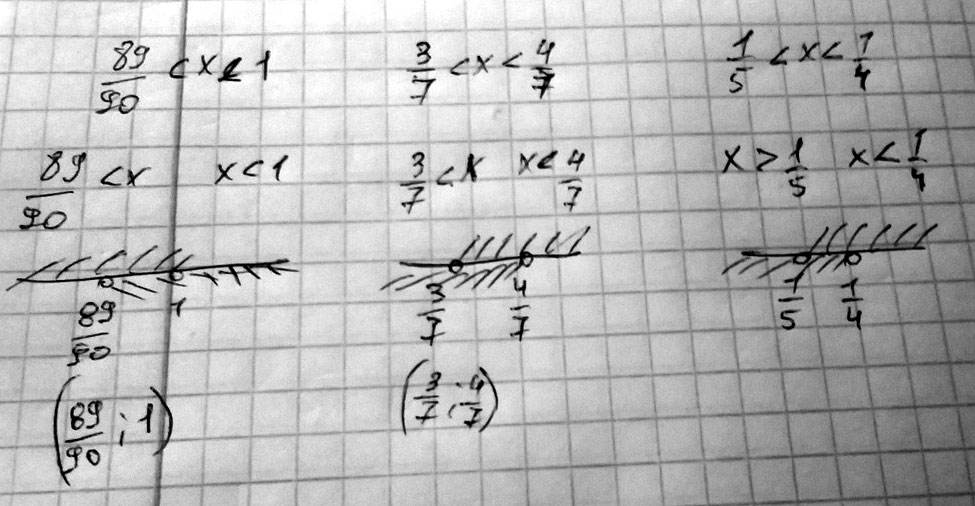
Найдите решение неравенства $$ {\frac{x + 3}{x^2 - x}} - {\frac{x + 5}{x + x^2}} > \frac{x - 6}{1 - x^2} $$
Решение: ОДЗ: х≠0 х≠1 х≠-1
После упрощения выражения получаем квадратное уравнение х²-6х+8
D = 4, x₁=2 x₂=4
(x-2)(x-4)>0. Имеем две системы неравенств:
х-2>0 x>2 x-2<0 x<2
x-4>0 x>4 x∈(4;+∞) x-4<0 x<4 x∈(-∞;2).
Учитывая ОДЗ решение неравенства будет иметь следующий вид:
х∈(-∞;-1)∨(-1;0)∨(0;1)∨(1;2)∨(4;+∞).Найдите решение неравенства с однозначным числом в знаменателе: 5/7< х < 6/7
Решение: Я думаю, что она решается так:
чтобы найти х, будем увеличивать знаменатель, умножая его на 2, на 3 и т.д.
1) умножаем на 2: 5/7=10/14, а 6/7=12/14. между ними стоит число 11/14, но его невозможно сократить так, чтобы получилось неравенство с однозначным числом в знаменателе.
2) умножаем на 3: получаем дроби 15/21 и 18/21. между ними дроби 16/21 и 17/21. но при сокращении тоже не получается неравенство с однозначным числом в знаменателе.
3) умножаем на 4: получаем 20/28 и 24/28. между этими дробями находятся числа 21/28, 22/28 и 23/28. последние отбрасываем, т.к. они не подходят.
выбираем дробь 21/28. сокращаем ее на 7, получаем 3/4.
вот так, я думаю, логичнее всего решить эту задачуНайдите решение неравенствах+2-х в квадрате
_________________ > или = 0
х в кубе + 1
Решение: 1) система: X+2-X^2>=0
X^3+1>0
а)X+2-X^2>=0
D=1+8=9
X=(1-3)/(-2)=1
X=(1+3)/(-2)=(-2)
X принадлежит (минус ∞; -2]и[1; плюс∞)
б)X^3+1>0
x^3>(-1)
x>(-1)
общее решение системы X принадлежит[1; плюс ∞)
2) система: X+2-X^2<=0
X^3+1<0
а)X^2-X^2<=0
X=1
X=(-2)
X принадлежит [-2; 1]
б)X^3+1<0
X^3<(-1)
X<(-1)
общее решениесистемы X принадлежит [-2; -1)
Решениевсего неравенства: X принадлежит [-2; -1) и [1; плюс ∞)
Ответ: : X принадлежит [-2; -1) и [1; плюс ∞)Найдите решение неравенства: x+6(4x-7)≤2(x-3)-10
Решение: $$ x+6(4x-7) \leq 2(x-3)-10 $$
$$ x+24x-42 \leq 2x-6-10 $$
$$ x+24x-2x \leq 42-10-6 $$
$$ 23x \leq 26 |:23 $$
$$ x \leq 1\frac{3}{23} $$
Ответ: $$ х∈(-∞; 1\frac{3}{23}) $$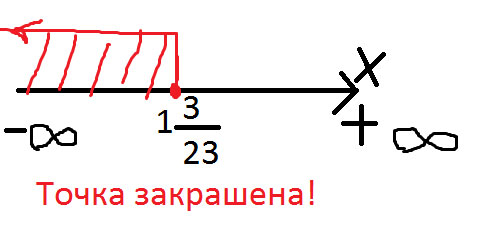

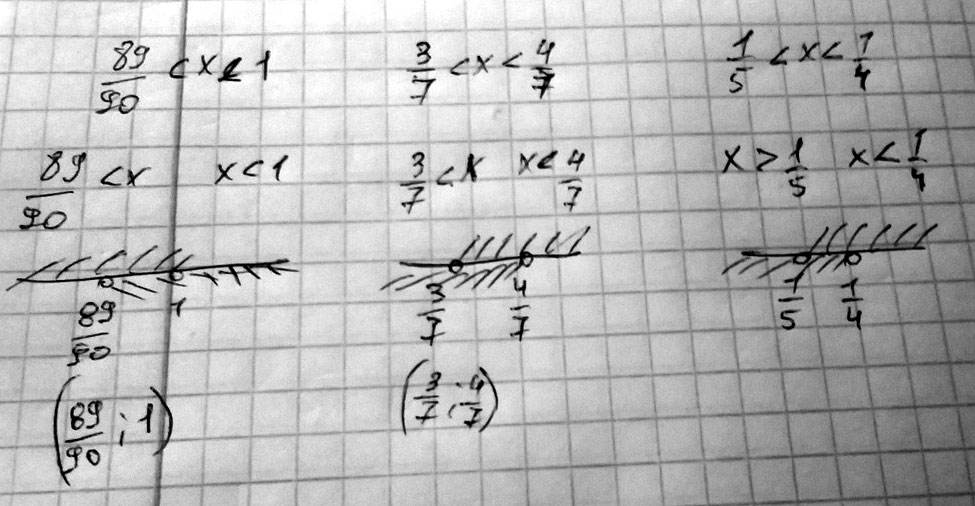

 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...