неравенства »

решите неравенство используя график - страница 2

  • Как решать неравенство, используя график? Например, решите неравенство х^2 > 4x используя график x^2-4x=y


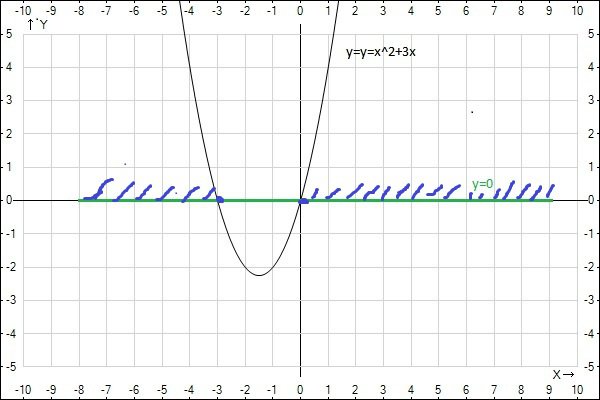
    Решение: Неравенство x^2>4x нужно привести к виду x^2-4x>0, после этого строим график у=х^2-4х и смотрим при каких значениях х он пересекает ось х. Все значения х, при которых график находится выше оси х будут удовлетворять условию неравенства, т.е. в данном случае х находится в области от - бесконечности до 0 и от 4 до + бесконечности 

  • на рисунке изображен график функции y=x^2+3x. Используя график, решите неравенство x^2+3x больше или равно 0


    Решение: Объяснение:

     x^2+3x>=0 - это можно записать как два графика и построить их в одной системе координат:

    1.y=x^2+3x

    2.y=0 -это прямая ,совпадающая с осью абсцисс.

    И решение будут те промежутки когда первый график будет "выше" или "на" втором графике.

    Ответ:x=(-<><>;-3]U[0;+<><>)

    Объяснение  x x - это можно записать как два графика и построить их в одной системе координат .y x x .y -это прямая совпадающая с осью абсцисс. И решение будут те промежу...

  • На рисунке изображен график функции y=x^2-6x+5.
    Используя график, решите неравенство x^2-6x+5>0


    Решение: Y=x²-6x+5
    график функции представляет из себя параболу с ветвями, направленными вверх. Неравенство x²-6x+5>0 означает, что значения  функции должны быть > 0, т.е смотрим ту часть графика функции,  которая расположена выше оси OX (где y>0) и соответствующие  значения х
    y>0, если x∈(-∞;1)∨(5;+∞)  

  • Дан график функции у=х^2-3х.Используя этот график, решите неравенство х^2-3х>0.


    Решение: Исходный график:
    Из этого графика видно, что решением этого неравенства является объединение двух промежутков: от минус бесконечности до 0 и от 3 до плюс бесконечности

    Исходный график Из этого графика видно что решением этого неравенства является объединение двух промежутков от минус бесконечности до и от до плюс бесконечности...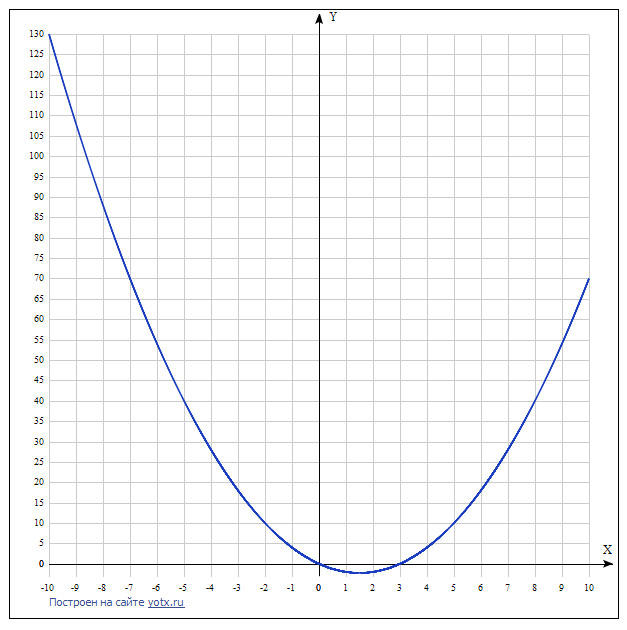

  • На рисунке изображен график функции y=x^2-4x. Используя рисунок, решите неравенство x^2<4x


    Решение: Решение ниже в приложении, где из рисунка видно, что
    Ответе:
    $$ 0

    Решение ниже в приложении где из рисунка видно чтоОтвете...
<< < 12 3 > >>