неравенства »
решите неравенство под корнем - страница 2
Решите неравенство √30-x-x² > -1 ( выражение 30-x-x² полностью под корнем)
Решение: Возводим в квадрат обе части неравенства
30 - х -х² > 1
- х² - х + 30 - 1 > 0
- х² - х + 29 > 0
Умножаем (- 1) обе части неравенства
х² + х - 29 > 0
Решаем квадратное уравнение
х²+х - 29 = 0
Д = 1+116 = 117
Дальше во вложении
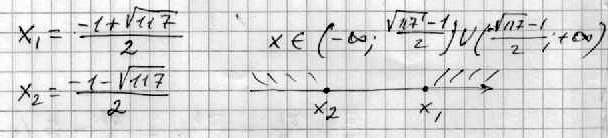
Решить неравенство: корень x^2+10x+9>=x^2-2x-3 (Левая часть вся под корнем)
Решение: Корень(x^2+10x+9) >=(x^2-2x-3)
одз х>= -1 или х<= -9
(x^2-2x-3)=(x-3)(х+1)<=0 при -1 <= х <= 3 участок [-1;3] входит в ОДЗ и значит входит в ответ
при остальных х выражение
(x-3)(х+1) >0
корень((x+9)(х+1)) >=(x-3)(х+1)
((x+9)(х+1)) >=((x-3)(х+1))^2
((x+9)(х+1))-((x-3)(х+1))^2 >= 0
метод интервалов
((x+9)(х+1))-((x-3)(х+1))^2 >= 0(х+1)*((x+9)-(x-3)^2*(х+1)) >= 0(х+1)*(x+9-x^3+5x^2-3x-9) >= 0-x*(х+1)*(x^2-5x+2) >=0
x^2-5x+2
d=25-4*2=17
x1=(5-корень(17))/2~0,438447
x2=(5+корень(17))/2~4,561552813
-х*(х+1)*(x-x1)*(x-x2) >=0
решаем методом интервалов
-беск_-1_0_x1_x2_беск
______.__.__.__.______
____(-).(+).(-).(+).(-)____
получаем ответ
интервалы [-1;0];[x1;x2] - являются решением, оба входят в ОДЗ
х є { [-1;0]U[(5-корень(17))/2;(5+корень(17))/2]U[-1;3]} =>
х є { [-1;(5+корень(17))/2]} - это ответ1) В правильной треугольнгой перамиде боковое ребро 41 а сторона основания 40корней из 2
Найти объем перамиды
2)Около шара радиус равен 3 описан цилиндр найти площадь боковой поверхности цилиндра.
3) решить неравенство
Дробь:
4^× -2/1-3x>0
(Четыре в степени икс минус два делить один минус три икс больше нуля)
Решение: 1) V = 1/3 *S(осн.)*H Площадь равностороннего треугольника равна а²√3/4.
S = (40√2)²*√3/4 = 800√3.
Проекцией бокового ребра на плоскость основания является радиус описанной окружности, R = a/√3 = 40√2/√3 = 40*√(2/3). Высоту найдем по теореме Пифагора: Н = √(41² -(40*√(2/3)² = √(1843/3).
V = 1/3 * 800√3 * √(1843/3) = 800√1843/3.
2) Радиус описанного цилиндра равен радиусу шара, а высота цилиндра - диаметру шара. R = 3, H=6.
S=2πR(R+H) = 2π*3*(3+6) = 54π.
3) (4^x-2)/(1-3x)>0. Решаем методом интервалов:
1.1-3х ≠0, х≠1/3.
2. 4^x-2 = 0 2^(2x) = 2, 2x=1, x=1/2.
Делаем чертеж:
____________1/3________1/2_________________х
- + -
Ответ:х∈(1/3; 1/2).Решить неравенства а) 4x+5( под кв. корнем)( меньше или равно) 0,5 б) 25-х( во 2 степени) ( все под кв. корнем)<4
Решение: 1)4x+5( под кв. корнем)( меньше или равно) 0,5
Т. к. 4х+5 должно быть больше или равно 0, то
0(больше или равно)4x+5(меньше или равно)0,25
-5(больше или равно)4x(меньше или равно)-4.75
-1.25(больше или равно)x(меньше или равно)-1.1875
Ответ[-1,25;-1,1875]
2)(25-х)(В квадрате)<4
-2<25-x<2
-2-25<-x<2-25
-27<-x<-23
23<x<27
Ответ:(23;27)

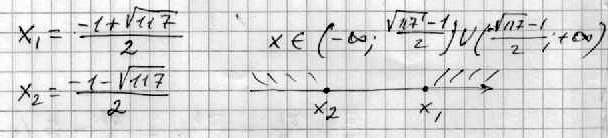
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...