решить неравенство показательное - страница 2

Решит неравенство(показательное) 2×>(1/2)²×⁻³ ( ×, ²×⁻³ степени)

Решение: 2^x>2^(-2x^(-2))

x>-2x^(-2)

x>-2/(x^2)

(x^3+2)/x^2>0

x≠0 x^3=-2 ___-______________+_______________+________

х=корень кубический из(-2) кор. куб.(-2) 0 х

ответ: (кор. куб.(-2);0) U (0;+∞)
Решить показательные неравенства (с полным решением) 1) 1/3x≥27 (× степень) 2) 2×>(1/2)²×⁻³ ( ×, ²×⁻³ степени)

Решение: $$ 1) (\frac{1}{3})^x \ge27 (\frac{1}{3})^x \ge (\frac{1}{3})^{-3} \\ x \le-3 \\ x \in(-\infty;-3] \\ 2) 2^x>(\frac{1}{2})^{2x-3} \\ x>-2x+3 \\ 3x>3 \\ x>1\\ x \in(1;+\infty) $$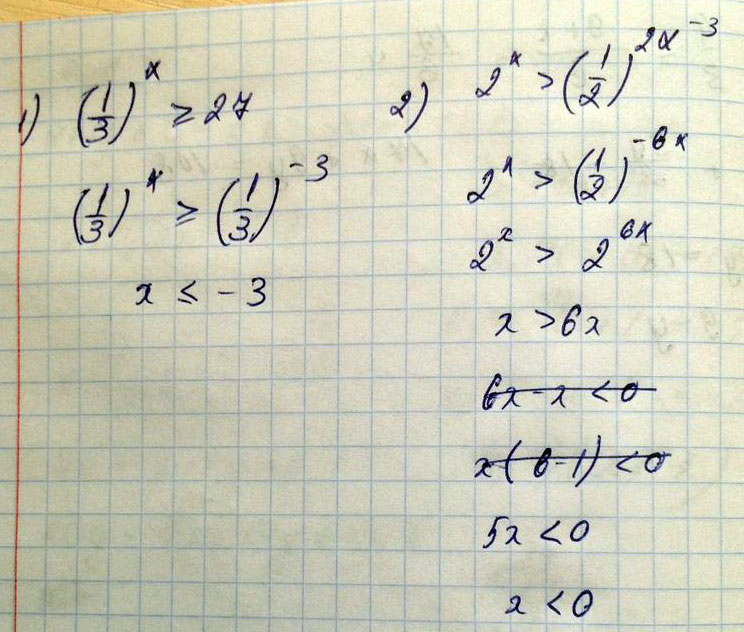
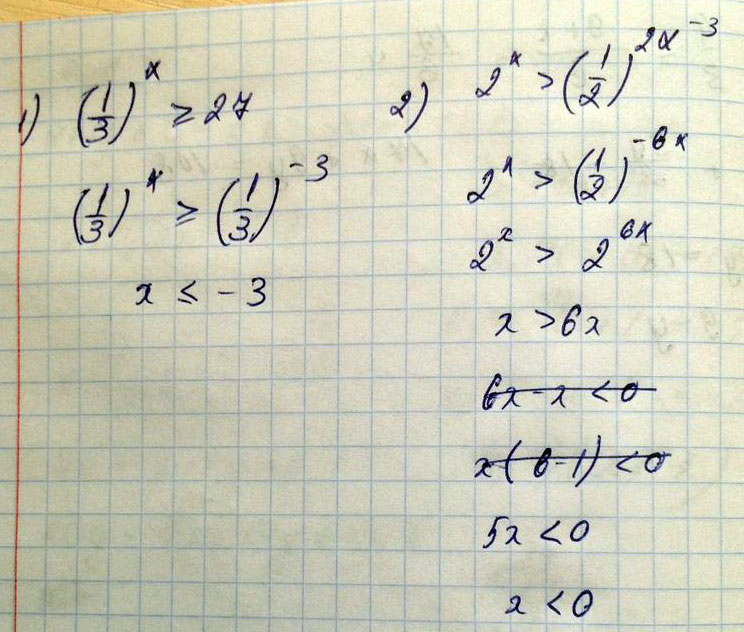
$frac x ge frac x ge frac - x le- x in - infty - x frac x- x - x x x x in infty...$

<< < 12