решите неравенство с помощью графика
Решите неравенство с помощью графика соответсвующей квадратичной функции х2-3х-4>0
Решение: $$ x^2-3x-4=y $$Квадратичная функция.
График-парабола,ветви направлены вверх.
Решая квадратное уравнение,находим точи пересечения с Ох,это -1 и 4
Т.к. ветви направлены вверх и парабола два раза пересекает Ох,значит вершина ниже Ох.Отрицательные значения функция принимает между корнями,то есть [-1;4]
$$ (-\infty;-1) \cup (4;+\infty) $$ - это больше нуля
Решите неравенство с помощью графика квадратичной функции
3 пример: x в квадрате +7x+10<0
4 пример: -x в квадрате + 3x-2>0
Решение: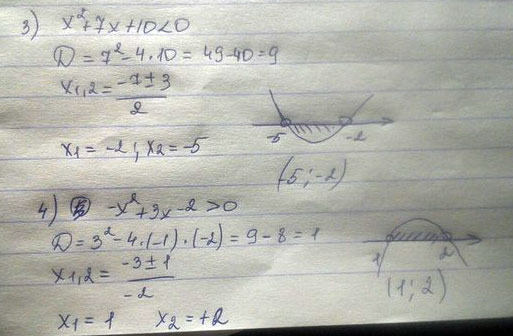
Решите неравенство с помощью графика соответствующей квадратичной функции
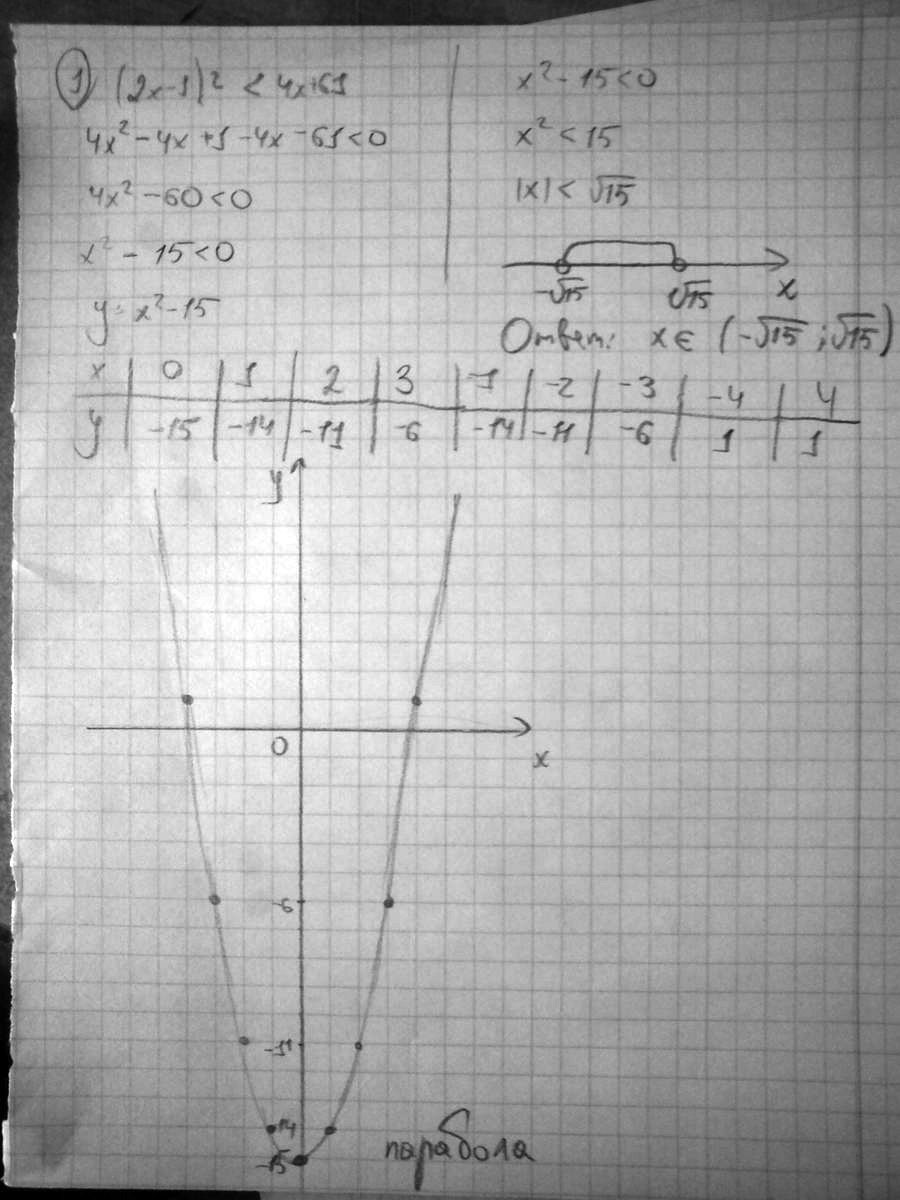
1)(2х-1)²<4x+61
2) -3(x+1)²≥3x-39
И еще:(все под корнем)
1)√9-144х²
2)√36-4х-х²
Решение: Смотри графики.Первый график это первое неравенство. Решение (-3,5).
Второй график это второе неравенство. Решение $$ x\in[\frac{-3-\sqrt{57}}{2};\frac{-3+\sqrt{57}}{2}] $$
ОДЗ первого $$ 9-144x^2\geq 0\\ 9\geq 144x^2\\ -3\geq 12x\geq 3\\ -1/4\geq x\geq 1/4 $$
ОДЗ второго $$ 36-4x-x^2\geq 0 $$ или $$ x\in[x_1,x_2] $$, где $$ x_1, x_2 $$ корни квадратного уравнения 36-4x-x^2=0.
Как решить с помощью графика неравенство-3х+6>0
Решение: Для начала определяемся с графиком (У=-3Х+6): перед нами прямая
Как ее строить:
для построения прямой необходимо найти 2 точки, подставляем, получается, что Х=0 соответствует У=6, Х=1 соответствует У=3
а вообще, если попрактиковаться, то сразу можно увидеть:
1) коэффициент отрицательный - угол тупой
2) коэффициент = -3 - одному делению х соответствует 3 деления у
3) свободный член (тот, что без переменной Х) = 6 - график пересекает ось ординат (ОУ) в точке х=0,у=6решите неравенства с помощью графика соответствующей квадратичной функции:
1) (2х-1)^2<4x+61
2)-3(х^2+1)≥3х-39
3)6х^2-5x≥-1/4x^2-1
4)2+1/8x^2<3x-x^2
Решение: 1) (2х-1)^2<4x+61 4x^2-4x+1-4x-61<0 4(x-5)(x+3)<0 x<5 и x<-34x^2-8x-60=0
D=64+960=1024
x1= 8+32
8
x1=5
x2=8-32
8
x2=-3
2)-3(х^2+1)≥3х-39 -3x^2-3-3x+39≥0 -3(x+3)(x-4)≥0 x≥-3 и х≥4
-3x^2-3x+36=0
D=9+432=441
x1=-3+21
-6
x1=-3
x2=-3-21
-6
x2=4

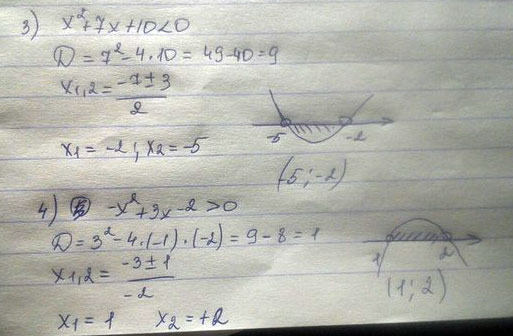


 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...