решить неравенство через дискриминант - страница 2

Как решить квадратное неравенство? Если через дискриминант не решается?

$$ 3+4x+8x^2=3+4x+(2\sqrt{2})^2x^2=3+4x+(2\sqrt{2}x+1)^2-1-4\sqrt{2}x $$=

Значит выражение под корнем надо выбрать так, чтобы члены с х оказались в скобке, для этого надо вместо единицы в скобке написать $$ \frac{1}{ \sqrt{2} } $$


$$ =(2\sqrt{2}x+\frac{1}{\sqrt{2}})^2-\frac{1}{2}+3=(2\sqrt{2}x+\frac{1}{\sqrt{2}})^2+2,5 $$

Заметим, что выражение в скобках всегда неотрицательно. А если прибавить 2,5, то все выражение всегда будет положительно.

То есть неравенство 
$$ 3+4x+8x^2<0 $$ не имеет решения

3x^2-2x+1<0 Решить неравенство. Знаю что дискриминант будет отрицательным.

Если дискриминант отрицательный ---> корней НЕТ)))
а корни --- это точки, лежащие на оси ОХ --- точки пересечения графика этой функции с осью ОХ (а график здесь --- парабола)))
и что значит, что корней НЕТ?? --- значит, график эту ось НЕ пересекает...
т.е. парабола либо ВСЯ выше оси ОХ, либо вся ниже оси ОХ...
осталось рассмотреть направление ветвей параболы...
старший коэффициент > 0 (3 > 0) ---> ветви ВВЕРХ, т.е. ВСЯ парабола выше оси ОХ (иначе парабола пересечет ось ОХ)))
а вопрос (знак неравенства): когда парабола НИЖЕ оси ОХ
Ответ: никогда (пустое множество решений)

РЕШИТЕ НЕРАВЕНСТВО С ЧЕРТЕЖОМ И ДИСКРИМИНАНТОМ: -3x^2+2x-1(больше или равно)0.

$$ 3x^2-2x+1\leq0 $$

3x^2 -2x+1=0

D=2^2 -4*1*3=4-12=-8

Дискриминант оказался отрицательным, поэтому решение этог онеравенства будем определять по правилу:

Если дискриминант < 0, знак неравенства < 0(вторая строчка решения, я разделил на -1, поэтому знак поменял), коэффициент а>0, то уравнение не имеет корней.

Эти правила определяются по схематическому графику.

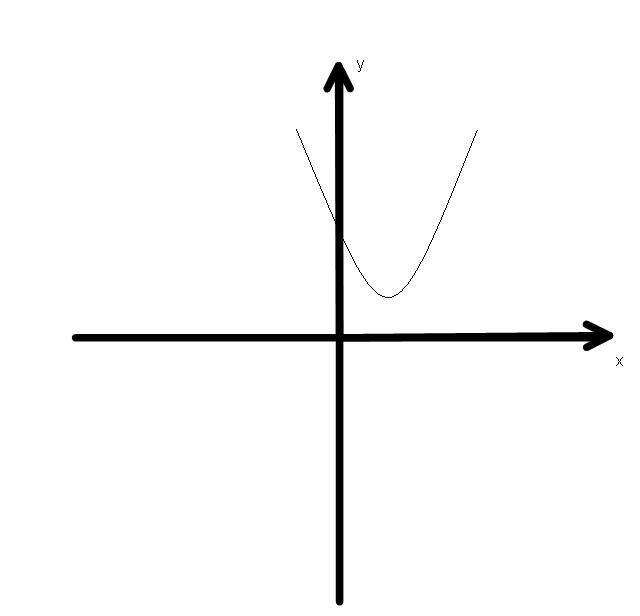
Решите неравенства через дискриминант: 2х^2 - х - 15>0. Второе: х^2<16.Третье: х^3 - 2х^2 - 4х + 8<0

Решение квадратных неравенств 2x^2-9x+4≥0 решить через дискриминант