неравенства »
найдите наименьшее решение неравенства - страница 2
Найдите наименьшее натуральное решение неравенства: -х3+ 6х2 – 8х > 0
Решение: -x3+6x2-8x>0
-x(x2-6x+8)>0
x(x2-6x+8)<0
x2-6x+8=0 найдем решение
D=36-4*8=4
x1,2=(6+-2)/2=2;4
получились промежутки:
1) (-беск;0) его не рассматриваем, т.к. не принадлежит множеству натуральных чисел
2) (0;2) не подходит, т.к. -x3+6x2-8x<0 на этом промежутке, что не соответствует условию
3) (2;4) условию соответствует -x3+6x2-8x>0
минимальное и единственное натеральное решение на этом промежутке точка x=3
4) (4; +беск) не рассматриваем, т.к. мин. натуральное мы нашлиНайдите наименьшее натуральное решение неравенства: f’(x) > g’(x), если f(x) = x^3 + x - √2 и g(x) = 3x^2 + x + √2
Решение: F`(x)=3x²+1
q(x)=6x+1
3x²+1>6x>1
3x²-6x>0
3x(x-2)>0
x=0 x=2
+ _ +
-------------(0)--------------(2)---------------
x∈(-∞;0) U (2;∞)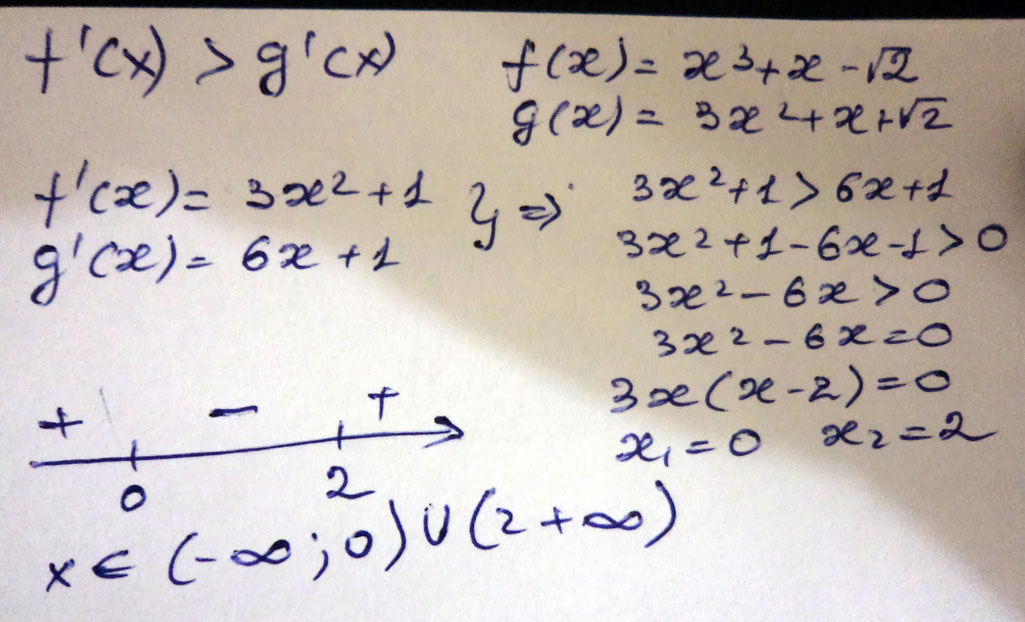
1)Найдите натуральное наименьшее решение неравенства: |x-6|≤8
2)Найдите наименьшее значение функции: y=18/x² +x²/2
3)Решите уравнение: $$ (0,25)^{2-x}=1/ 2^{(x+3)} $$
Решение: 1) это неравенство равносильно: -8 <= x-6 <= 8
или: -2 <= x <= 14
наименьшее натуральное решение: 1
2)) если найти производную и приравнять ее к нулю, получим абсциссы точек экстремумов функции: -36/(x^3) + x = 0
x^4 = 36 ---> x^2 = 6 ---> x = +- V6
y(+V6) = y(-V6) = 18/6 + 6/2 = 3+3 = 6
3) нужно привести все к одному основанию...
0.25 = 1/4 = 2^(-2)
(2^(-2))^(2-x) = 2^(2x-4)
1/2^(x+3) = 2^(-x-3)
2x-4 = -x-3
3x = 1
x = 1/3Найдите наименьшее целое решение неравенства (x+7)( x^ 2 +10x +21) / x^ 4 - 49x^ 2 ≥ 0
Решение:X²+10x+21=0
x1=-7
x2=-3
по теореме Виета
значит
x²=10x+21=(x+7)(x+3)
в знаменателе
x²(x²-49)=x²(x-7)(x+7)
ОДЗ(делить на ноль нельзя)
x≠0
x≠7
x≠-7
$$ \frac{(x+7)(x+7)(x+3)}{ x^{2} (x-7)(x+7)} \geq 0 \\ \ \frac{(x+7)(x+3)}{ x^{2} (x-7)} \geq 0 \\ x^{2} \geq 0 \\ \ x+7=0 \\ x=-7 \\ \ x=3=0 \\ x=-3 \\ \ x-7=0 \\ x=7 $$
- + -
......-7 ///////////////////-3................7......
x∈(-7;-3]
Наименьшее целое решение неравенства х=-6.
Ответ:х=-6.

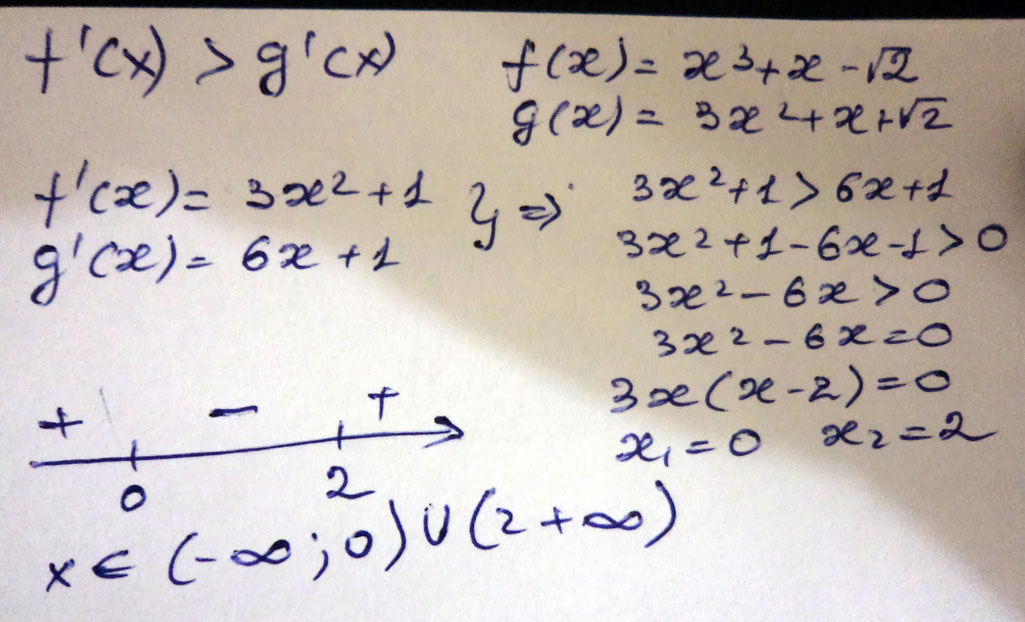
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...