неравенства »

найти решение системы неравенств - страница 2

  • x+3 /5 - x-2/4 меньше или равно 1 5х+8 меньше или равно 38 это одно неравенство(система) нужно найти середину промежутка, служащего решением системы неравенств


    Решение:

    $$ \begin{cases} \frac{x+3}{5}-\frac{x-2}{4}\leq1 \\ 5x+8\leq38 \end{cases} $$

    $$ \begin{cases} \frac{4(x+3)-5(x-2)-20}{20}\leq0 \\ 5x\leq30 \end{cases} $$

    $$ \begin{cases} 4x+12-5x+10-20\leq0\\x\leq6 \end{cases} $$

    $$ \begin{cases} -x+2\leq0\\x\leq6 \end{cases} $$

    $$ \begin{cases} x-2\geq0\\x\leq6 \end{cases} $$

    $$ \begin{cases} x\geq2\\x\leq6 \end{cases} $$

    Выпишем все целые решения системы: 2,3,4,5,6

    Ответ: 4

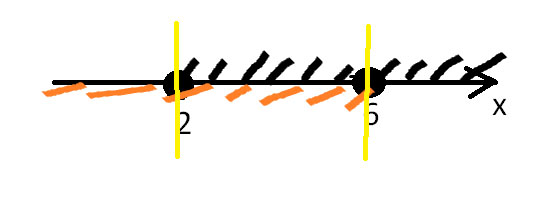
    begin cases frac x - frac x- leq x leq end cases begin cases frac x - x- - leq x leq end cases begin cases x - x - leq x leq end cases begin cases -x leq x leq end...

  • Найти длину интервала, задающего все решения СИСТЕМЫ неравенств $$ \left \{ {{-1<1-2x<2} \atop {(2\sqrt{2}-3)(5x-3)>0}} \right. $$


    Решение:

    Решаем первое двойное неравенство

    $$ -1 < 1-2x < 2 \\ \left\{ {{1-2x > -1} \atop {1-2x < 2}} \right. \\ 1-2x > -1 \\ -2x > -2 \\ x<1 \\ 1-2x<2 \\ -2x<1 \\ x>-0,5 $$

    Решаем второе неравенство.

    Важно обратить внимание на первую скобку, в ней нет аргумента, но нужно посмотреть, больше или меньше она нуля.

    внесем двойку и тройку под корни и увидим что √8-√9 <0 => (2√3-3)<0

    Теперь смело отметаем эту скобку, но при решении 5x-3 помним, что знак нужно будет поменять.

    $$ 5x-3<0\ 5x<3\ x<0,6 $$

    И так вышли решения:

    x<1; x>-0,5; x<0,6

    Объединяем их и получаем:

    $$ x \in (-0,5; \\ 0,6) $$

    Длинна интервала находится как разность правой и левой границы

    $$ 0,6-(-0,5)=1,1 $$

    Ответ: 1,1.

  • Решить систему неравенств с одной переменной: \( \left \{ {{\frac{1,4-x}{5}-\frac{0,6x}{3}<2,28} \atop {\frac{2x-1}{7}-1} > \frac{x}{3}} \right. \)


    Решение: $$ \left \{ {{\frac{1,4-x}{5}-\frac{0,6x}{3}<2,28} | \cdot 15 \atop {\frac{2x-1}{7}-1} > \frac{x}{3}| \cdot 21} \right. \\ \left \{ {{3(1,4-x)-5(0,6x)<2,28\cdot{15}} \atop {3(2x-1)-21>7x}} \right.\\\left \{ {{4,2-3x-3x<34,2} \atop {6x-3-21-7x>0}} \right.\\\left \{ {{-6x<30} \atop {-x>24}} \right.\\\left \{ {{x>-5} \atop {x<-24}} \right. $$

    Видим, что множество решений первого неравенства не пересекается с множеством решений второго неравенства, значит система не имеет решения. х принадлежит пустому множеству.

  • Найти все а, при каждом из которых система неравенств имеет 1 решение. Система объединяет 2 неравенства:
    (x-a)^2+y^2<=25a^2
    3x+4y<=12


    Решение: Первое неравенство - это круг, с центром в точке (a;0); R=5a
    Второе неравенство - это плоскость ограниченной прямой $$ 3x+4y-12 $$
    Прямая так же проходит через точки $$ (4;0)\ U \\ (0;3) $$. Можно сказать что радиус будет большим, так как уже известно, что по оси центр будет точка 0, а что бы сама система имела единственное решение, достаточно чтобы это прямая была касательной к окружности. То есть система неравенство переходит в систему уравнений.
    $$ \left \{ {{(x-a)^2+y^2=25a^2} \atop {3x+4y=12}} \right. \\ \left \{ {{(x-a)^2+(\frac{12-3x}{4})^2=25a^2} \atop {y=\frac{12-3x}{4}}} \right. \\ 25x^2-x(32a+72)-384a^2+144=0 \\ D=\sqrt{(32a+72)^2+100(384a^2-144)}=0 \\ a=-\frac{6}{11} $$
    То есть когда дискриминант равен 0, корень один 
    при a=-6/11
    $$ x=\frac{12}{11}; y=\frac{24}{11} $$

<< < 12