найдите целочисленное решение неравенства - страница 2
Найдите такое целочисленное значение параметра p, при котором множество решений неравенства (x+2)(p-x)>=0
а) целых четыре числа
б) два натуральных числа
в) два целых числа
г) одно целое число
Решение: Корнями уравнения (x+2)(p-x)=0 будут x=-2 и x=p
При любом значении параметра p графиком функции y=(x+2)(p-x) будет парабола ветвями вниз. Т.е. функция будет положительна на отрезке между корнями и отрицательна вне этого отрезка.
Начнём с варианта г.
Одно целое число в ответе уже есть - это -2.
Также целочисленным ответом является значение x=p (т.к. по условию p - целое). Значит, ровно одно целое число будет в том случае, если эти 2 решения совпадают. А это будет в том случае, если p=-2.
в). 2 целых числа будут в случае, если p≠-2, и при этом на отрезке между p и -2 нет целых значений. Это будет в том случае, если -2 и p - соседние целые числа. Отсюда p=-1 или p=-3.
а). 4 целых числа означает, что кроме решений x=-2 и x=p есть еще 2 решения. Т.е. длина отрезка между -2 и p равна 3.
|p-(-2)|=3
|p+2|=3
p+2=3 или -(p+2)=3
p=1 или p=-5
Если p=1, то решениями будут x=-2; x=-1; x=0 и x=1
Если p=-5, то решениями будут x=-2; x=-3; x=-4 и x=-5
в). 2 натуральных числа означает, что на отрезке между -2 и p есть ровно 2 натуральных значения. Т.к. -2 < 0, то p должно быть положительным. Однако в этом случае натуральными значениями на отрезке могут быть только значения 1 и 2. Причем последнее и должно быть p.
Ответ:
a) p=-5 (x∈(-2;-3;-4;-5)) или p=1 (x∈(-2;-1;0;1))
б) p=2 (x∈(-2;-1;0;1;2))
в) p=-1 (x∈(-2;-1)) или p=-3 (x∈(-2;-3))
г) p=-2 (x=-2)Найдите целочисленные решения неравенства: (x+9)(x-11)^2(x-12)<0
Решение: Сначала берём скобки и по отдельности узнаем, что за х. Далее строим прямую и ставим на ней выколотые точки. Определяем знаки. Нам подходит -, т.к. изначальное выражение меньше 0.
х принадлежит (-9;11);(11;12)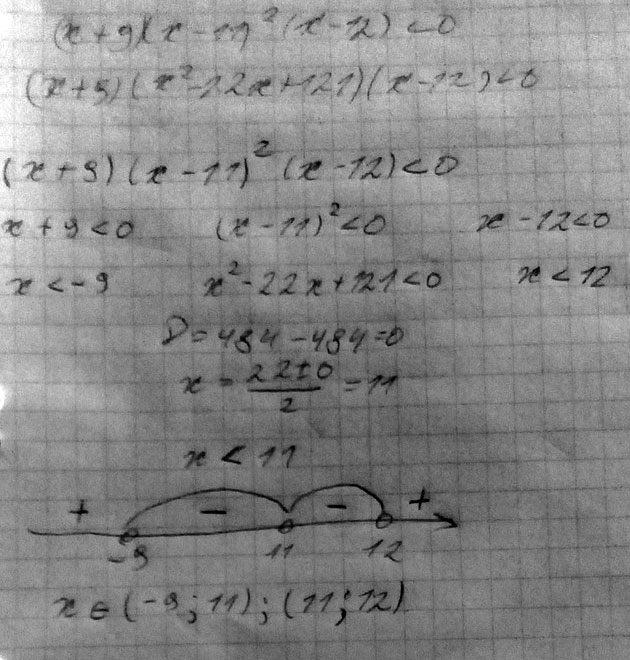
Найдите сумму целочисленных решений неравенства log₀,₅(x²-7x+12) больше log₀,₅(x+5)
Решение: Log(0.5, x^2-7x+12) > log(0.5, x+5)
ОДЗ: x^2-7x+12 > 0, x+5 > 0
x^2-7x+12 > 0 => (x-3)(x-4)>0 => x∈(-∞;3)∪(4;+∞)
x+5 > 0 => x∈(-5;+∞)
Отсюда получаем ограничения на x: x∈(-5;3)∪(4;+∞)
Решаем само неравенство. Так как основания логарифмов равны между собой и меньше 1, то справедлив переход к неравенству:
x^2-7x+12<x+5
x^2-8x+7<0
(x-1)(x-7)<0
x∈(1;7)
С учетом ОДЗ, x∈(1;3)∪(4;7)
Целочисленные решения: 2, 5, 6.
2+5+6=13.
Ответ:13.0<0,5<1,
х²-7х+12<х+5;
х²-8х+7<0; х1=1; х=7,
1<х<7.
Ответ:х∈(1; 7).найдите количество целочисленных решений неравенства $$ \frac{2x^2-3x-2}{x^2-7x+10} < 0 $$
Решение:$$ \frac{2x^2-3x-2}{x^2-7x+10}<0 \\ 2x^2-3x-2=2(x-2)(x+1/2) \\ D=(-3)^2-4*2*(-2)=9+16=25=5^2 \\ x_1=2 \\ x_2=-1/2 \\ \frac{2(x-2)(x+1/2)}{(x-2)(x-5)}<0 $$
+ - - +
___________-1/2__________2_____________5__________
{0;1;3;4}-целочисленные решения неравенства. Всего их 4
Ответ: 4найдите колличество целочисленных решений неравенства|7x-2|>9 на отрезке [-4;4]
Решение:7x-2>9 7x>11 x>11/7
7x-2>=0 7x>=2 x>=2/7
2-7x>9 7x<-7 x<-1
7x-2<=0 7x<=2 x<=2/7
[-4;4] = -4; -3; -2; 2; 3; 4
|7x-2|>9
$$ \left \{ {{7x-2\geq0} \atop {7x-2>9}} \right. $$
или
$$ \left \{ {{7x-2<0} \atop {2-7x>9}} \right. $$
х принадлежит $$ (\frac{11}{7};+\infty) $$
или
х принадлежит $$ (-\infty;-1) $$
Решение неравенства: (-$$ (-\infty;-1)\cup(\frac{11}{7};+\infty) $$
Т.о.. целочисленных решений на отрезке [-4;4] шесть (-4,-3,-2,2,3,4)

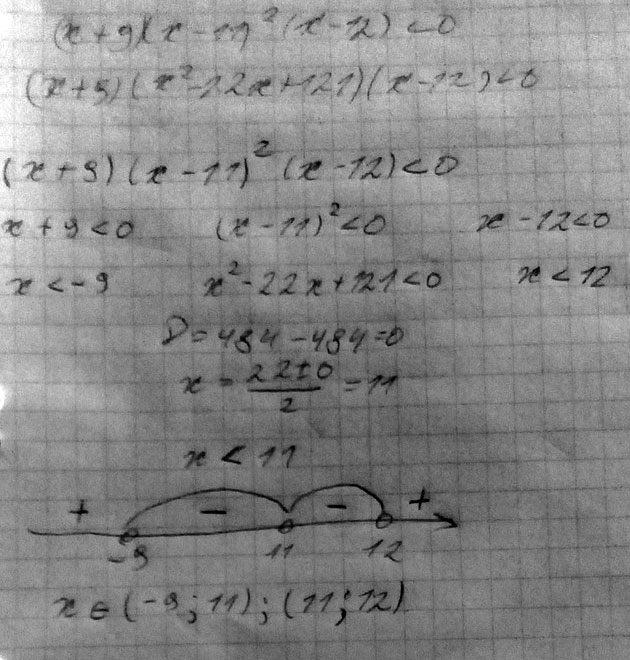
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...