найти сумму решений неравенства - страница 2
Найти сумму целых решений неравенства: 2x^2-5x-3<0
Решение: 2x²-5x-3<0
2x²-5x-3=0
D=b²-4ac=25-4*2*(-3)=25+24=49
x₁=$$ \frac{-b+ \sqrt{D} }{2a}= \frac{5+7}{4}=3 $$
x₂=$$ \frac{-b- \sqrt{D} }{2a}= \frac{5-7}{4}= -\frac{2}{4}=- 0,5 $$
2x²-5x-3=(x-3)(x+0,5)
Ответ: (-0,5;3)
Целые решения: -1, 0, 1, 2.
Их сумма: -1+0+1+2=2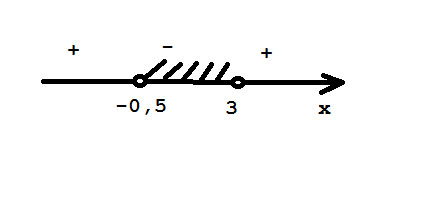
Найти сумму целых решений неравенства |х-7|(36-х2)больше либо равно 0
Решение:Модуль любого выражение $$ \geq 0 $$ .Поэтому заданное произведение будет $$ \geq 0 $$ ,если второй множитель тоже $$ \geq 0 $$.
$$ |x-7|(36-x^2) \geq 0\\1)\; \; |x-7| \geq 0\; pri \; \; \; x\in R\\|x-7|=0\; \; pri\; \; x=7\\2)\; \; 36-x^2 \geq 0\; \; \Rightarrow \; \; x^2-36 \leq 0\\(x-6)(x+6) \leq 0\\+++(-6)---(6)+++\\x\in[\, -6,6\, ]\\3)\; \; \left \{ {{x=7} \atop {x \un [\, -6,6\, ]}} \right. \; \; \Rightarrow \; \; x\in [\, -6,6\, ]U\{7\} $$
Целые решения неравенства: х=-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7.
Сумма этих чисел равна 7.
|х-7|(36-х²)≥0 + - + -
Система: ------------------------------->
(х-7)(36-х²)≥0 ⇔ (х-7)(6-х)(6+х)≥0 -6 6 7 x
(7-х)(36-х²)≥0 (7-х)(6-х)(6+х)≥0 - + - +
---------------------------------->
-6 6 7 x
x=-6;6;7
-6+6+7=7
отв:7Найти сумму целых решений неравенства х квадрат+3х-1 меньше 0
Решение:X^2 + 3x - 1 < 0
D = 3^2 - 4(-1) = 9 + 4 = 13
x1 = (-3 - корень(13))/2 ~ -3,3
x2 = (-3 + корень(13))/2 ~ 0,3
x = (x1; x2) ~ (-3,3; 0,3)
Целые решения: -3, -2, -1, 0
Их сумма равна -6Умножим на -1,неравенство меняет знак
х^2_3*х+1<0
Ищем корни:
х1,2 = (3+-sgrt(5))/2
Решение - больше меньшего, меньше большего корней то есть:
((3-sgrt(5))/2;(3+sgrt(5))/(2)Найти сумму целых решений неравенства (1 - x)|x^2 + x - 12| >= 0 на промежутке [-2;4]
Решение: Модуль всегда не меньше нуля, потому имеет смысл найти только точки равенства нулю.
x^2 + x - 12 = 0
x1 + x2 = -1
x1 * x2 = -12
x1 = -4, x2 = 3
Эти точки входят в общее решение, но не влияют на знак выражения при нахождении его методом пробной точки.
1 - x = 0
x = 1
+ _
-------------- 1 ------------
Т.о. нам подходят все точки x <= 1 и точки x = -4, x = 3
На промежутке [-2, 4] это точки
-2, -1, 0, 1, 3
А их сумма, как не трудно посчитать, равняется 1.
Найти сумму целочисленных решений неравенства log три (х-3) <или =1 - log три (х-1)
Решение: $$ \log_3(x-3) \leq 1-\log_3(x-1)\ \log_3(x-3) \leq \log_3 \frac{3}{x-1} $$
Так как основание 3>1 (функция возрастающая), знак неравенства не меняется
$$ \begin{cases} & \text{ } x-3 > 0 \\ & \text{ } x-1 > 0 \\ & \text{ } x-3 \leq \frac{3}{x-1} \end{cases}\Rightarrow \begin{cases} & \text{ } x > 3 \\ & \text{ } x > 1 \\ & \text{ } \frac{x^2-4x}{x-1} \leq 0 \end{cases}\Rightarrow\begin{cases} & \text{ } x > 3 \\ & \text{ } x \leq 0;\,1 < x\leq 4 \end{cases}\Rightarrow 3 < x \leq 4 $$
$$ x \in (3;4]. $$
Сумму не вычислить) так как в промежуток входит число 4
Ответ: 4

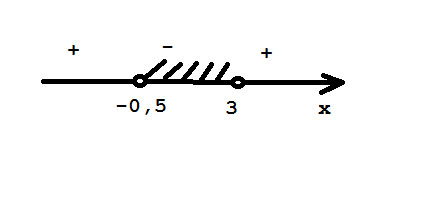
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...