неравенства »

найти все целые решения неравенства

  • Указать все значения параметра m, при каждом из которых любое число является решением неравенства x^2-5x+m > 0


    Решение: Рассмотрим функцию f(x)=x²-5x+m. Это парабола с ветвями вверх. Она имеет наименьшее значение, которое достигается в вершине параболы при x=-(-5)/2=2.5. Соответственно, если наименьшее значение функции f(x) будет строго больше 0, то и все остальные значения функции при других аргументах тоже будут больше 0.
    f(2.5)=2.5²-5*2.5+m=m-6>0 => m>6
    Ответ: m>6.

  • Найти наименьшее целое решение неравенства 36^x-2*18^x-8*9^x<0


    Решение: 6^2x-2*6^x*3^x-8*3^2x<0/3^2x
    (6/3)^2x-2*(6/3)^x-8<0
    2^x=a
    a²-2a-8<0
    a1+a2=2 U a1*a2=-8
    a1=-2 U a2=4
    -2<a<4
    -2<2^x<4
    x<2
    x∈(-∞;2)

    $$ 36^x-2\cdot18^x-8\cdot9^x < 0|:36^x\ 1-2\cdot( \frac{1}{2})^x-8\cdot( \frac{1}{4} )^x < 0 $$

    $$ 1-2\cdot( \frac{1}{2})^x-8\cdot( \frac{1}{4} )^x=0 $$
     Сделаем замену $$ ( \frac{1}{2})^x=t $$

    решив уравнение, получим ответ х=2

    ___-___(2)____+____

    Решение неравенства x<2

  • Найти все целые решения неравенства 2x(в квадрате)+х-6<(или равняется)0


    Решение: Перед нами квадратное неравенство 2х² + х -6 ≤ 0.

    Для начала решим квадратное уравнение 2х² + х -6 

    Решаем квадратное уравнение

    x 1 = -2
    x 2 = 1.5

    Интервалы знакопостоянства
    Определяем интервалы, на которых функция не меняет знак - интервалы знакопостоянства. 
    ( -∞, -2) ( -2, 1.5) ( 1.5, +∞) 

    Определяем, какой знак принимает функция на каждом интервале. 
    ( -∞, -2) плюс 
    ( -2, 1.5) минус 
    ( 1.5, +∞) плюс 

    Записываем интервалы, удовлетворяющие неравенству. 
    ( -2, 1.5)

    Проверяем входят ли концы интервалов в ответ. 
    [-2, 1.5]
     ФИНАЛЬНЫЙ ОТВЕТ: 
    x принадлежит интервалу [-2, 1.5]

    А нам в ответ нужно записать ТОЛЬКО ЦЕЛЫЕ ЧИСЛА

    Ответ: -2; -1; 0; 1.

  • Найти все целые решения неравенств 1/6<6^(3-x)<36


    Решение: 1/6 < 6 ^ ( 3 - х ) < 36
    6 ^ - 1 < 6 ^ ( 3 - х ) ^ 6 ^ 2
    - 1 < 3 - х < 2
    - 4 < - х < - 1
    4 > х > 1
    Ответ ( 1 ; 4 )

  • Найти наибольшее целое решение неравенства (5-x)*(x^2-6x+5)/(x^3-25) больше или равно 0


    Решение: 1. Рассмотрим функцию и определим область определения функции

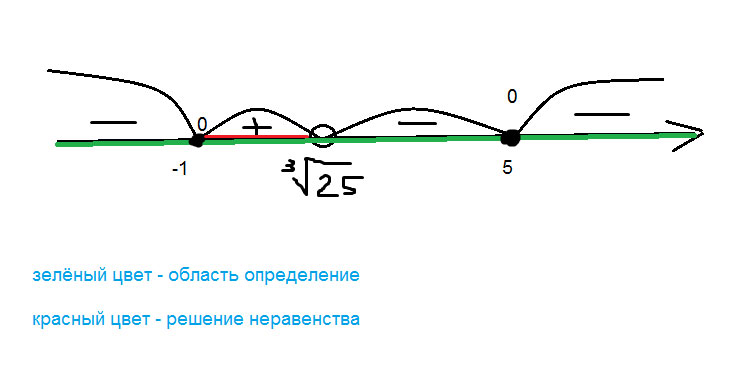
    $$ y= \frac{(5-x)(x^2-6x+5)}{x^3-25} \\ x^3-25 eq 0 \\ x eq \sqrt[3]{25} \\ D(y)=(-\infty;\sqrt[3]{25})U(\sqrt[3]{25};+\infty) $$

    1. Определим нули функции

    $$ \frac{(5-x)(x^2-6x+5)}{x^3-25} =0 \\ (5-x)(x^2-6x+5)=0 \\ 5-x=0 \\ x_1=5 \\ x^2-6x+5=0 \\ D=b^2-4ac=(-6)^2-4*1*5=36-20=16 \\ \sqrt{D} =4 \\ x_2= \frac{-b+ \sqrt{D} }{2a} = \frac{6+4}{2} =5 \\ x_3= \frac{-b- \sqrt{D} }{2a} = \frac{6-4}{2} =1 $$

    3. Знаки на промежутке (смотреть во вложения)

    Решение неравенства - [1;∛25) U {5}

    Наибольшее целое будет 5

    Ответ: 5.

    //////////////////////////////////////////////////////////////////////////
    . Рассмотрим функцию и определим область определения функции y frac -x x - x x - x - eq x eq sqrt D y - infty sqrt U sqrt infty . Определим нули функции frac -x x - x x - -x...