дроби »
дробь умножить на дробь - страница 2
(х+3)умножить на 4=(х-9)умножить (-2) - уравнение.. разложите на множители 16х в квадрате минус 49..
а в шестой степени умножить на а в квадрате, дробная черта, а в 4 степени.
Решение: Если я правильно поняла условие, то
(х+3)*4=(х-9)*(-2)
4x+12=-2x+18
4x+2x=18-12
6x=6
x-1
--------------------------------------
(1+3)*4=(1-9)*(-2)
4*4 = -8*(-2)
16=16
16x^2-49 = (4x+7)(4x-7)
a^6*a^2 a^6+2 a^8
-------------- = --------------- = ------------ = a^8 : a^4 = a^8-4 = a^4
a^4 a^4 a^4Найдите значение выражения. 1) (одна пятая) в минус двадцать пятой степени умножить на 25 в минус шестой степени умножить на 125 в минус четвёртой степени. 2) 6 в минус десятой степени,дробная черта, 81 в минус второй степени умножить на 32 в минус второй степени. 3) 20 в минус четвёртой степени умножить на 15 в минус третьей степени, дробная черта, 30 в минус седьмой степени. В первом должно получится 5, во втором 1/9, в третьем 40,5.
Решение: Вот решение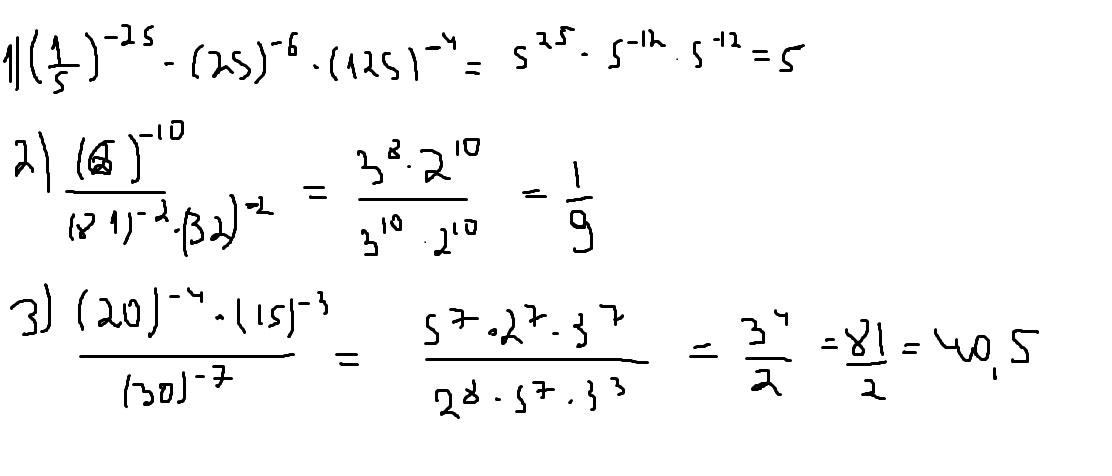
Нужно сократить алгебраические дроби: ^ - степень. * - умножить. \\ - дробная черта.
1) 36a^3b^2c-36a^3b^3\48ab^5-48ab^3c^2
2) (m-n)^2\m^2-n^2
3) 6pq-18p\(q-3)^2
4) c^2-18c+81\c-9
5) 5-2m\4m^2-20m+25
6) b^2-49\49-14b+b^2
7) 4n^2-4nm+m^2\4n^2-m^2
8) a^2-ab-b-c^2\b^2-a^2+2ac-c^2
9) x^2-yz+xz-y^2\x^2+yz-xz-y^2
10) 8^11-8^10-8^9\4^15-4^14-4^13
11) 87^3+43^3\87^2-87*43+43^2
Решение: 1) 36a^3b^2c-36a^3b^3\48ab^5-48ab^3c^2 = = 36a^3b^2(c - b) / 48ab^3(b^2-c^2) = 3a^2(c-b) /4(b-c)(b+c) =
= -3a^2/4b(b+c)
2) (m-n)^2\m^2-n^2 = (m-n)^2 / (m-n)(m+n) = (m-n)/(m+n)
3) 6pq-18p\(q-3)^2 = 6p(q - 3)/(q - 3)^2 = 6p/(q-3)
4) c^2-18c+81\c-9 = (c-9)^2 / (c-9) = c - 9
5) 5-2m\4m^2-20m+25 = (5 - 2m)/(5-2m)^2 = 1/(5-2m)
6) b^2-49\49-14b+b^2 = (b-7)(b+7)/(b-7)^2= (b+7)/(b-7)
7) 4n^2-4nm+m^2\4n^2-m^2 = (2n-m)^2 / (2n-m)(2n+m) =(2n-m)/(2n+m)
8) a^2-ab-bс-c^2\b^2-a^2+2ac-c^2 = [(a^2-c^2) - b(a+c)] / [b^2 - (a-c)^2] =
= [(a-c)(a+c) - b(a+c)] / [(b-(a-c)(b+(a-c)] = [(a+c)(a-c-b)]/ [-(a-c-b)(a+b-c)]=
= -(a+c)/(a+b-c)
9) x^2-yz+xz-y^2\x^2+yz-xz-y^2 = = [(x^2-y^2) - z(x-y)] / [(x^2-y^2) - z(x-y)]=1
10) 8^11-8^10-8^9\4^15-4^14-4^13 = 8^4(1-1^6-1^5) / 4^12(1^3-1^2-1) =
= 8^4 (1-1-1)/4^12(1-1-1) = 8^4/4^12
11) 87^3+43^3\87^2-87*43+43^2 =
= (87+43)(87^2-87*43+43^2)/(87^2-87*43+43^2) =(87+43) = 130Представьте в виде степени с основанием 2: 4^(-n) умножить на 4^(2n);
16^(8n)/16^(2n);
(0,25)^-3)^n
/ - дробь
^ - степень
Решение: $$ 4^{-n} \cdot 4^{2n}=2^{-2n} \cdot 2^{4^{n}}=2^{2^n} \\ 16^{6^n}=(2^4)^{6^n}=2^{2^{4^n}} \\ ((1/4)^{-3})^n=(4^3)^n=2^{6^n} $$
Сравнить значения выражений:(7дробь4)в 5 степени умножить (4дробь7)в 4 степени и (-2) в 0 степени
Решение: $$ (\frac{7}{4} )^{5} * ( \frac{4}{7} )^{4} =(\frac{7}{4} )^{5}*( \frac{7}{4} )^{-4} = \frac{7}{4} $$
$$ -2^{0} =1 $$
$$ \frac{7}{4} >1 $$
1 Этап
Пусть первая сторона будет x
Тогда вторая будет y
$$ \frac{x}{y} = \frac{7}{6} $$
S-площадь будет равна $$ S=xy=168 $$
2 этап
$$ \frac{x}{y} = \frac{7}{6} \\ 6x=7y \ x= \frac{7y}{6} $$
$$ xy=168 \\ \frac{7 y^{2} }{6}=168 \\ y^{2} =144 \\ y=12 \\ x= \frac{168}{y} = \frac{168}{12} =14 $$
3 этап
Стороны прямоугольника соответственно равны 12 и 14 см

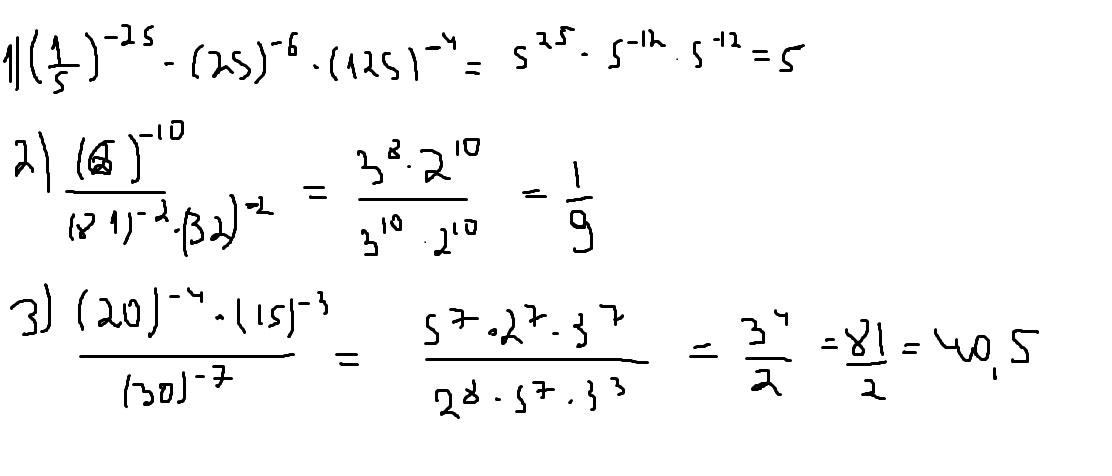

 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...