график функции »

график касательной к функции - страница 2

  • К графику функции y=x^2+2x-3 проведены касательные в точках (0;-3) и (-2;-3). Найдите координаты точки пересечения этих касательных


    Решение: Yk = f(xo)+f’(xo)(x-xo).
    1) xo(0;-3).
      f(xo) = -3.
      f’(x) = 2x+2.
      f’(xo) = 2*0+2 = 2
      yk = -3+2(x-0) = 2x-3.
    2) xo(-2;-3).
      f(xo) = 4-4-3 = -3.
      f’(x) = 2x+2.
      f’(xo) = -4+2 = -2
      yk = -3-2(x+2) = -3-2x-4 = -2x-7.
    Точка К пересечения: 
      2х-3 = -2х-7
      4х = -4
      х = -4/4 = -1.
      у = 2*(-1)-3 = -2-3 = -5.
      К(-1; -5).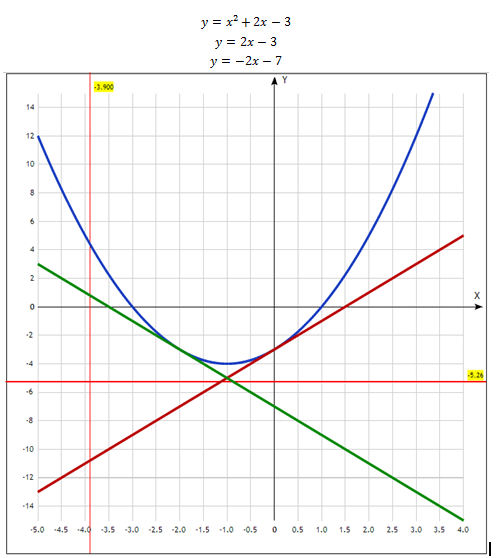 

    Yk f xo f xo x-xo . xo - .  f xo - .  f x x .  f xo   yk - x- x- .  xo - - .  f xo - - - .  f x x .  f xo - -   yk - - x - - x- - x- .Точка К пересечения    х- - х-   х -   х...

  • К графику функции у=корень (х+2) проведена касательная, образующая с осями координат треугольник наименьшей площади. Найдите координаты точки касания.


    Решение: D(y)=[-2;+∞)- область определения данной функции.
    Cоставим уравнение касательной к кривой в точке z
    y(z)=√(z+2);
    y’(x)=1/2√(x+2)
    y`(z)=1/2√(z+2)
    Уравнение
    у-у(z)=y’(z)(x-z)
    y-√(z+2)=(x-z)/2√(z+2)
    Найдем точки пересечения касательной с осями координат
    При х=0  у=√(z+2)-(z/2√(z+2))=(2z+4-z)/2√(z+2)=(z+4)/2√(z+2)
    При у=0  x-z=-2(z+2)  ⇒x=-z-4
    Треугольник, образуемый касательной с осями координат- прямоугольный, с катетами |-z-4|  и |(z+4)/2√(z+2)|
    Площадь прямоугольного треугольника находим по формуле как  половину произведения катетов:
    S(Δ)=(1/2)|-z-4|·(z+4)/2√(z+2)=(z+4)²/4√(z+2)
    S’(z)=2(z+4)(3z+4)/16(z+2)√(z+2)
    S’(z)=0
    3z+4=0
    z=-4/3
    y(-4/3)=√((-4/3)+2)=1/√3
    О т в е т.(-4/3; 1/√3)

  • Дана функция f(x)=3+5x+3x^2. Найдите координаты точки её графика, в которой угловой коэффицент касательной к нему равен -7.


    Решение: касателная  ест  производной  функции  в точке.

     производная :

    (3+5x+3x²)’  = (3)’+(5x)’+(3x²)’  =  0 + 5 + 3 · 2x =  6x + 5

     искаем  аргументу  для которрого    6x + 5 = (-7)

     6x =( -7 ) -5 = -12

     x= (-2)

     тепер   найдем значение функцйии для этого аргумента

    y= 3+5x+3x²    где  x = (-2)  

    y= 3 + 5 · (-2) +  3 · (-2)²  = 3 + (-10) + 3· 4 = (-7) + 12=  5

    искана  точка, т=  ((-2), 5 )

     во вложению  граф, 

    касателная  y = (-7) x  +  C   по поводу  grafa  найдем  число  C

    5 = (-7)· (-2)+ C

    C= 5 - 14 = -9

    касателна  в точке  (-2, 5)  :    y= (-7) x - 9

    извините  лексикальное  граматические ошибки  я не русский

  • Найдите площадь треугольника, ограниченного осями координат и касательной к графику функции f(x)=кореньиз(5-4х), проведенной в точке его пересечения с прямой у=х.
    Решите с подробным объяснением


    Решение: Найдем точку пересечения графиков заданных функций:
    {y=√(5-4x)
    {y=x √(5-4x)=x; 5-4x=x^2; x^2+4x-5=0; x1=-5;x2=1
      x1=-5; √(5+20)=-5 неверно! 
      x2=1; √(5-4)=1 верно, х=1-корень уравнения
    тогда у=1, (1;1)-точка пересечения
    Составим уравнение касательной: f(x)=f(a)+f’(a) *(x-a); а=1
    f(1)=√(5-4*1)=1;
    f’(x)=(√(5-4x))’=1/(2√(5-4x)) *(5-4x)’=-4/ (2√(5-4x))=-2/√(5-4x);
    f’(1)=-2/√(5-4)=-2
    f(x)=1-2*(x-1); f(x)=-2x+2-уравнение касательной
    Найдём точки пересечения касательной с осями координат
    с осью х: y=0; -2x+2=0; -2x=-2; x=1
    с осью у: x=0; y=-2*0+2; y=2
    тогда имеем прямоугольный треугольник с катетами, длины которых1 и2
    S=1/2 *1*2=2/2=1
    Ответ. 1

  • 5) Найдите площадь треугольника, образованного осями координат и касательной к графику функции f (х) = 3х-2(корень из) х в точке с абсциссой х0 = 4


    Решение: Найдем уравнение касательной,  по формуле
      $$ y=f(a)+f’(a)(x-x_{0}) $$ 
     $$ f(4)=3*4-2\sqrt{4}=8\\ f’(x)=3-\frac{1}{\sqrt{x}}\\ f’(4)=3-\frac{1}{2}=\frac{5}{2}\\\\ y=8+\frac{5}{2}(x-4) = \frac{5x}{2}-2\\\\ $$
    Точки пересечения прямой с осями координат, равны 
    $$ OX=>\frac{5x}{2}-2=0\\ x=\frac{4}{5}\\ |OY|\\ => \frac{5*0}{2}-2=|2|\\\\ S=\frac{\frac{4}{5}*2}{2}=\frac{4}{5} $$

<< < 12 3 > >>