график функции »

абсцисса точки пересечения графика функции

  • 1)Определите не выполняя построение графика функции y=3/4x+9; a)координаты точек пересечения графика с осями координата; б) принадлежат ли графику точки:А(100;84;),В(-0,05;-7,9),С(-30;30,5) в)есть ли на графике точка, абсцисса которой равна её ординате.


    Решение: а) Пересечение с осью абсцисс: (то есть при \( x=0 \))

    $$ y=\frac{3}{4\cdot 0}+9 $$

    Икс принадлежит пустому множеству. 

    График не имеет точек пересечения с осью абсцисс.

     Пересечение с осью ординат: (то есть при \( y=0 \))

    $$ \frac{3}{4x}+9=0 $$;

    $$ 36x=-3 $$

    $$ x=-\frac{1}{12} $$

    Точка пересечения графика с осью абсцисс - \( (\frac{1}{12};0) \)

    б) А(100;84)

    Подставим значения:

    $$ 100 = \frac{3}{84\cdot 4}+9 $$

    Неверно. Не принадлежит.

    B (-0,05;-7,9)

    $$ -7,9 = \frac{3}{-0,05\cdot 4}+9 $$

    Неверно. Не принадлежит.

    C (-30;30,5)

    $$ 30,5 = \frac{3}{-30\cdot 4}+9 $$

    Неверно. Не принадлежит.

    в) $$ \frac{3}{4x}+9=x $$

    $$ 4x^2-36x-3=0 $$

    Ответ: да, таких точек даже две: \( (4,5-\sqrt{21};4,5-\sqrt{21}) \) и \( (\sqrt{21}+4,5;\sqrt{21}+4,5) \)

  • Найдите абсциссу точки пересечения графиков функции : y=( 1 дробная черта 3) в степени x, и y=9


    Решение: $$ \frac{1}{3} ^{x} $$ это функция выглядит как гипербола, но не затрагивает низ ординаты и ноль. 
    1) $$ \frac{1}{3} ^{x} = 9^{-1/2} $$ (к общему основанию)
    -x/2 = 1 ( 9 со второй части в первой степени).
    x=-2
    Это первый способ.
    2)
    Второй способ можно воспроизвести графически, просто подставляя икс.

  • Найдите координаты точки пересечения графика функции у=2-6х с осью абсцисс.


    Решение: Пересечение с осью абсцисс подразумевает, что у=0, следовательно нам необходимо решить простенькое уравнение
    2-6х=0
    -6х=-2
    х=1/3
    для иллюстрации график функции приложен

    Ось абсцисс это ось Х
    2-6х=0
    6х=2
    х=2/6=1/3
    ответ (1/3;0)

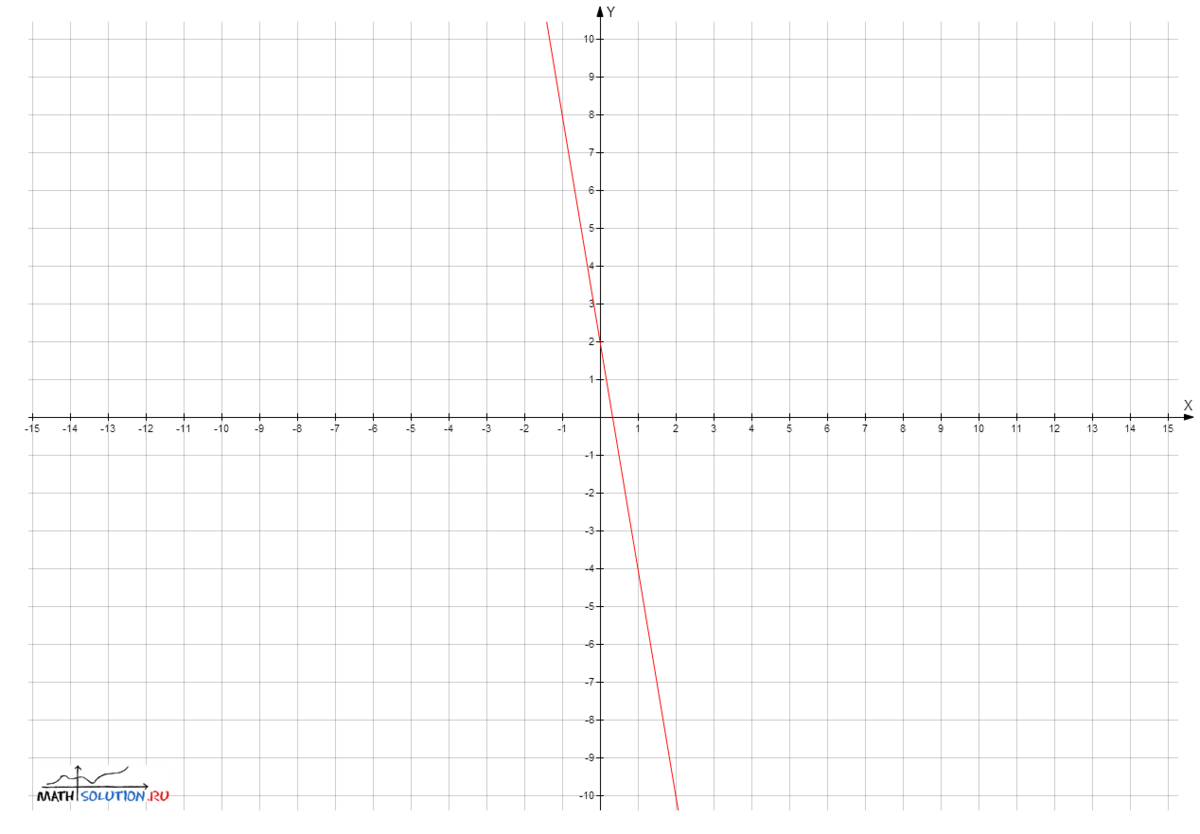
    Пересечение с осью абсцисс подразумевает что у следовательно нам необходимо решить простенькое уравнение - х - х - х для иллюстрации график функции приложен Ось абсцисс это о...

  • Функция задана формулой y=0,5x+2. Найдите координаты точки пересечения графика этой функции с осью абсцисс.
    1) (0;2)
    2) (2;0)
    3) (-4;0)
    4) (0; -4)
    Напишите сам ответ и решение)


    Решение: Во-первых, если функция пересекает ось абсцисс, то координата у=0. Таким образом, можно отбросить 1-е и 4-е решения. 

    Затем подставляем оставшиеся варианты в функцию, на место х ставим первое число, а на место у - второе.

    2=0,5*2+2

    2=3, значит эта точка не подходит

    0=0,5*(-4)+2

    0=0, значит эта точка подходит

    Ответ: 3

  • На рисунке изображены графики функций у=-х²+5 и у=-х+3. Найдите координаты точки пересечения этих графиков, имеющий большую абсциссу


    Решение: $$ \left \{ {{y=-x^2+5} \atop {y=-x+3}} \right. \\ -x+3=-x^2+5\\ x^2-x-2=0\\ D=1+8=9=3^2\\ x_{1,2}= \left \{ {{(1-3)/2} \atop {(1+3)/2}} \right. = \left \{ {{-1} \atop {2}} \right. $$ 
    ну и смотрим большую абсциссу. честно говоря не помню, но вроде где больший икс, значит это 2 подставляем в любое уравнение находим y
    ⇒ y=-4+5=1
    (2,1) координаты нужной точки

  • Постройте график функций y=4x-8, найдите координаты точки пересечения графика с осью абсцисс


    Решение: Если функция пересекает ось абсцисс(то есть ось х), то у=00,25х-10=0 0,25х=10х=10:0,25х=40(40,0)-ответ

    У=4х-8
    Типа таблица
    х=1 у=-4
    х=2 у=0
    Потом я на координатной плоскости отмечаю точки (1;-4) и (2;0) 
    Провожу прямую. Горизонтальная линия и есть ось абсцисс. А эта прямая, которую я провёл тот самый график у=4х-8
    Ну а пересекаются они в точке А (Можно любую букву) координаты которой (2;0) 0_0