исследовать на экстремум функцию - страница 2
Докажите, что функция является чётной1)y=-xв4 степени+8xв квадрате
2)y=xв кубе- 1:x дробью
Решение: Если подставить например число 2
то получить 16+256 числа четные и функция чётная
да и вообще если степень 2,4,6,8,10 то четная если 1,3,5 и тд то не чётнаяфункция четная если f(x)=f(-x)
1)y=-xв4 степени+8xв квадрате
f-(x)=-(-x)^4+8(-x)^2=-x^4+8x^2=f(x) четная
2)y=xв кубе- 1:x дробью
f(-x)=((-x)^3-1)/(-x)=-(x^3+1)/-x=(x^3+1)/x не четная и не неяетнаяИсследовать на максимум и минимум функцию y= -x(в4 степени)+2x(во 2 степени)+1
Решение: Исследование на максимум и минимум функцииy=-x^4 +2x^2+1
Чтобы найти точки экстремума, нужно найти производную и приравнять к 0
y’=-4x^3+4x
y=0
-4x^3+4x=0
x^3-x=0
x(x^2-1)=0
x(x-1)(x+1) = 0
x = 0, x=1, x=-1 - точки экстремума,в которых производная меняет знак
Если y’ меняет знак с "+" на "-", то это точка максимума, если с "-" на "+", то точка минимума
y’=-4x^3+4x = -x(x-1)(x+1)
y’>0 при х (-∞;1) и (0;1)
y’<0 при х (-1;0) и (1;+∞)
Следовательно, x=-1 и x=-1 -точки максимумаx=0 -точка минимума
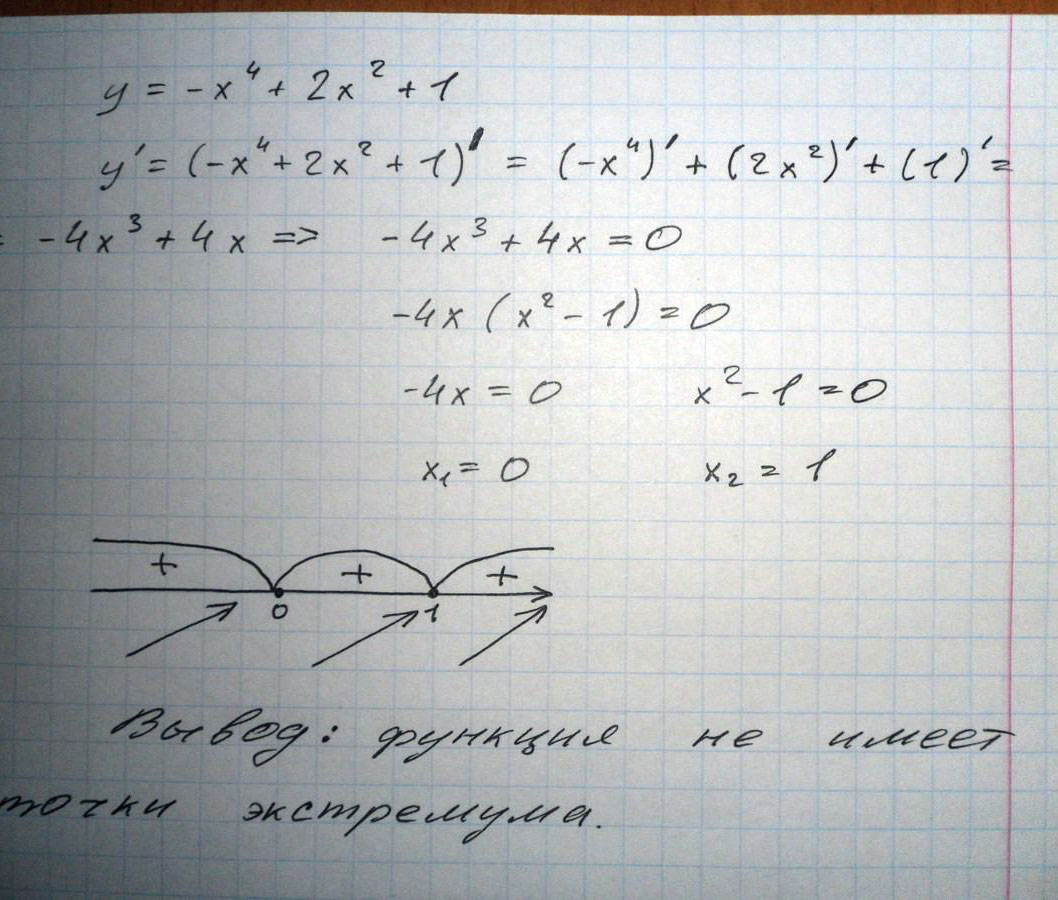
Найдите точку минимума функции y=(13-x)*e в степени 13-x
Решение: Решение
Находим первую производную функции:
y’ = -( - x + 13)e^(- x + 13) - e^(- x + 13)
или
y’ = (x -14)e^(- x + 13)
Приравниваем ее к нулю:
(x - 14) e^(- x + 13) = 0
e^(- x + 13) ≠ 0
x - 14 = 0
x = 14
Вычисляем значения функции
f(14) = 1/e
Используем достаточное условие экстремума функции одной переменной. Найдем вторую производную:
y’’ = (- x + 13)e^(- x + 13) + 2e^(- x + 13)
или
y’’ = (- x+15)e^(- x + 13)
Вычисляем:
y’’ (14) = (- 14+15)e^(- 14 + 13) = e⁻¹ = 1/e
y’’(14) = 1/e > 0 - значит точка x = 14 точка минимума функции.Определить четная или не четная функция.: y=3х(во второй степени)+1 y=3х( в второй степени)+х; y=5х (втретьей степени) y=5х( в третьей степени)+х
Решение: Функция является четной если y(-x)=y(x);Функция является нечетной если y(-x)=-y(x).
1) y(x)=3x^2+1
y(-x)=3(-x)^2+1=3x^2+1;
y(-x)=y(x), значит функция является чётной.
2)y(x)=3x^2+x
y(-x)=3(-x)^2+(-x)=3x^2-x.
Чётность функции определить нельзя.
3) y(x)=5x^3
y(-x)=5(-x)^3=-5x/
y(-x)=-y(x), значит функция является нечётной.
4) y(x)=5x^3+1
y(-x)=5(-x)^3+1=-5x^3+1.
Чётность функции определить нельзя.
1) Тело движется по прямой так что расстояние S от начальной точки
изменяется no закону S = 3t + t^2 (м), где t - время движения в секундах.
Найдите скорость тела через 3 с после начала движения.
2) Найти точки экстремума функции f(x) = 3 + 7x - 4х^2
3) Тело движется по прямой так, что расстояние S ( в метрах) от него до
точки В этой прямой изменяется по закону S(t) = 2t^3 - 6t^2 + 6 (t - время
движения в секундах). Чему будет равно ускорение, через 2 секунды
движения?
4) Дана функция f(x) = 2x^2 - х + 1. Найти координаты точки ее графика, в котором угловой коэффициент касательной к нему равен 7.
5) Исследовать функцию на выпуклость и точки перегиба f(x) = 2х^3 + 9x^2 - 24x.
Решение: 1) Тело движется по прямой так что расстояние S от начальной точки изменяется no закону S = 3t + t² (м), где t - время движения в секундах.
Найдите скорость тела через 3 с после начала движения.
Решение:
Найдем функцию скорости как производную от функции расстояния по времени:
$$ v= \frac{dS}{dt}=( 3t+t^2)’=(3t)’+(t^2)’=3+2t $$
Найдем значение скорости через 3 с после начала движения
V = 3 + 3² = 3 + 9 = 12 м/с
Ответ: 12 м/с
2) Найти точки экстремума функции f(x) = 3 + 7x - 4х²
Решение:
Найдем производную функции
f’(x) = (3 + 7x - 4х²)’ = (3)’ + (7x)’ - (4х²)’ = 0 + 7 - 4*2x = 7- 8x
Найдем критические точки
f’(x)=0 ⇔ 7-8x=0
8x=7
x=0,875
На числовой прямой отобразим эту точку и знаки производной полученные по методу подстановки. Например при х=0 f’(0)=7>0
+ 0 -
-
0,875
Функция возрастает на промежутке (-∞;0,875) так как производная на этом интервале числовой прямой больше нуля
Функция убывает на промежутке (0,875;+∞) так как производная на этом интервале числовой прямой меньше нуля
В точке х=0,875 функция имеет локальный максимум.
у(0,875) =3+7*0,875+4*(0,875)² = 12,1875
Ответ: х=0,875; y=12,1875 - максимум
3) Тело движется по прямой так, что расстояние S ( в метрах) от него до
точки В этой прямой изменяется по закону S(t) = 2t³ - 6t² + 6 (t - время
движения в секундах). Чему будет равно ускорение, через 2 секунды
движения?
Решение:
Найдем функцию скорости как производную функции расстояния
V(t) =S’(t) = (2t³ - 6t² + 6)’ = (2t³)’ - (6t²)’ + (6)’ =2*3t² -6*2t +0 = 6t² -12t (м/с)
Найдем функцию ускорения как производную скорости по времени
a(t) = V’(t) = (6t² - 12t)’ = (6t²)’ - (12t)’ = 6*2t -12 =12t - 12 (м/с²)
Найдем ускорение тела через 2 секунды после начала движения
а(2) =12*2-12=12 м/с²
Ответ 12 м/с²
4) Дана функция f(x) = 2x² - х + 1. Найти координаты точки ее графика, в котором угловой коэффициент касательной к нему равен 7.
Решение:
Угловой коэффициент касательной функции в точке равен производной функции в этой точке
Найдем производную функции
f’(x) = (2x² - х + 1)’ = 4x-1
Поскольку угловой коэффициент касательной равен 7 то можно записать, что
4х - 1 = 7
4х = 8
х = 2
f(2) = 2*2² -2+1 = 8 - 1 =7
Ответ: х=2; у=7
5) Исследовать функцию на выпуклость и точки перегиба f(x) = 2х³+ 9x² - 24x.
Решение:
Найдем первую производную функции
f’(x) = (2х³ + 9x² - 24x)’ =2*3x²+9*2x-24 = 6x² + 18x - 24
Найдем вторую производную функции
f"(x) = (6x² + 18x - 24)’ = 6*2x + 18 - 0 =12x+18
Найдем критические точки
f"(x)=0 ⇔ 12x+18 =0
12x = -18
x=-1,5
На числовой прямой отобразим эту точку и знаки второй производной
- 0 +
-
-1,5
Функция вогнута вниз на интервале х∈(-1,5;+∞) так как вторая производная больше нуля
Функция выпукла вверх на интервале х∈(-∞;-1,5) так как вторая производная меньше нуля
В точке х=-1,5 функция имеет точку перегиба
y(-1,5) = 2(-1,5)³+ 9(-1,5)² - 24(-1,5) = 49,5
Ответ: вогнута вниз на интервале х∈(-1,5;+∞) ; выпукла вверх на интервале х∈(-∞;-1,5); х=-1,5 y=49,5 точка перегиба

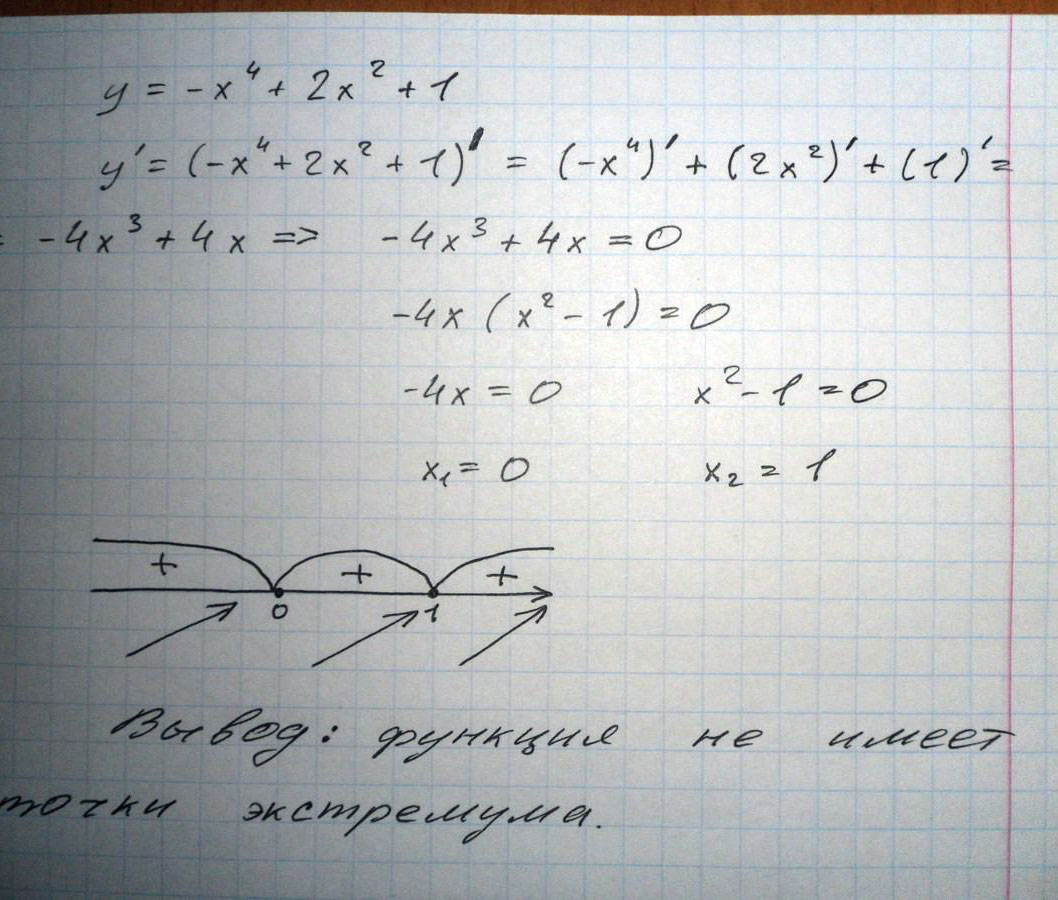
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...