дана функция y

Прямая L заданная уравнением у = ах (а > 0), делит квадрат ОАВС (О — начало координат, А(0; 4), С(4; 0)) на две фигуры. Задайте следующие функции f в зависимости от значения а:
а) f(a) — площадь фигуры, содержащей вершину А;
б) f(a) — площадь фигуры, содержащей вершину С;
в) f(a) — отношение, в котором прямая L делит площадь квадрата (считая от фигуры, содержащей точку А).

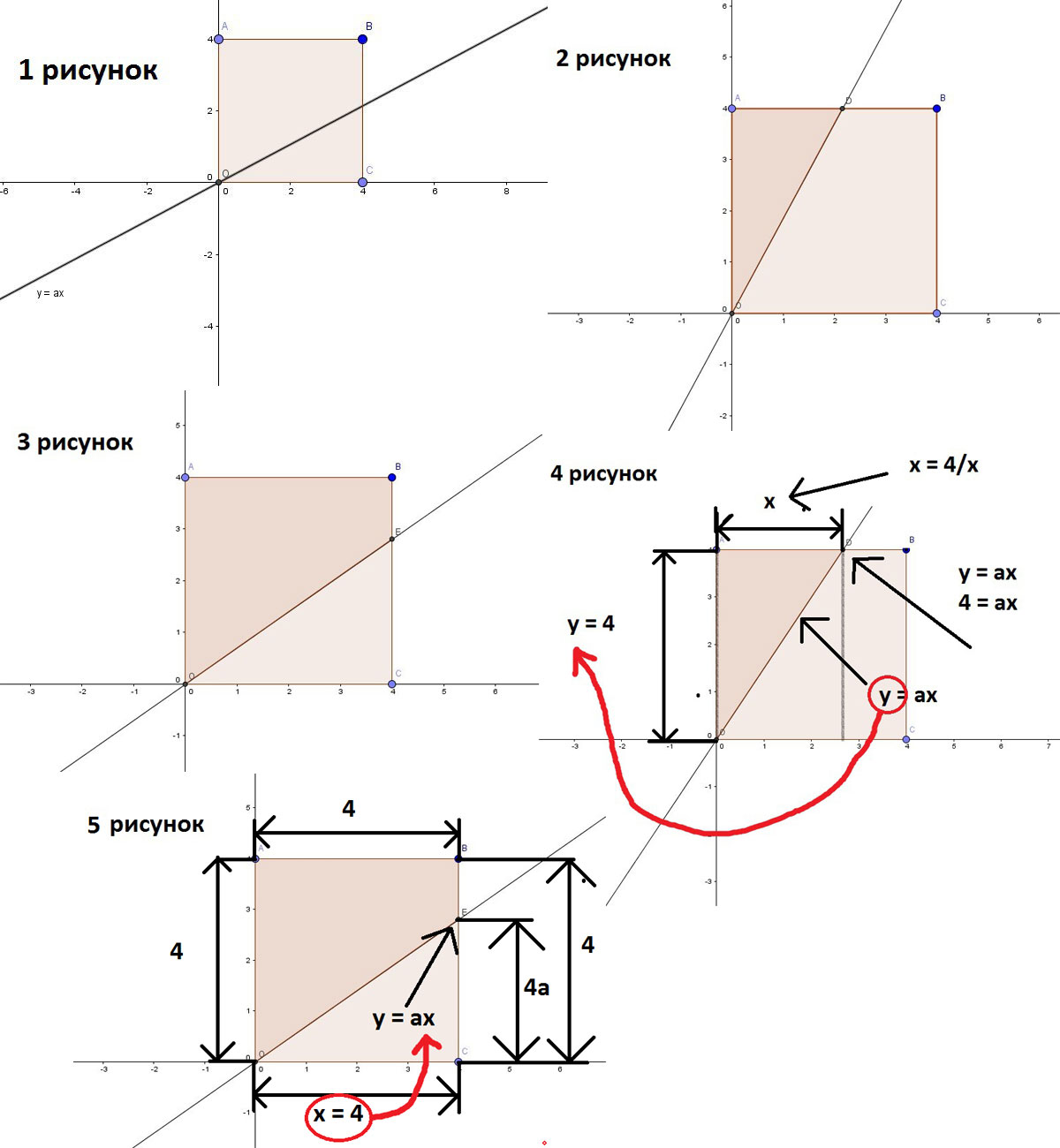
Дана функция f(x) где f(x)=x в -3 степени. Найдите все значения х, при которых выполняется неравенство х^2/f(x)>64*f(1/x)

Дана функция f(x) где f(x)=x в -3 степени.
Найдите все значения х при которых выполняется неравенство х в квадрате/f(x)>64*f(1/x)

х^2/(x^(-3))>64*(1/(x^(-3)))
x^(2+3)>64*x^3
x^5-64x^3>0
x^3(x^2-64)>0
x^3(x-8)(x+8)>0
Значения х при которых левая часть неравенства меняет знак
x=0 x+8=0 x-8=0
x=0 x=-8 x=8
На числовой прямой отразим знаки левой части неравенства
  -    0 + 0  -   0 +.
-------!--------!-------!-----
  -8 0 8   .
Поэтому неравенство имеет решение при
x принадлежит (-8;0)U(8;+бескон)

Дана функция f(x) где f(x)=x в -3 степени. Найдите все значения х при которых выполняется неравенство х в квадрате/f(x)>64*f(1/x)

$$ \frac{x^2}{f(x)} > 64 \cdot f(\frac{1}{x}) $$

для функции, заданной как $$ f(u) = u^{-3} $$.

В таком случае имеем

$$ \frac{1}{f(x)} = \frac{1}{x^{-3}} = x^3 $$

$$ f\left(\frac{1}{x}\right) = \left(\frac{1}{x}\right)^{-3} = x^3 $$

Упрощаем неравенство

$$ \frac{x^2}{f(x)} > 64 \cdot f(\frac{1}{x}) \; \Leftrightarrow \; {x}^2 \cdot {x}^3 > 64 \cdot x^3 $$

$$ {x}^5 - 64 \cdot x^3 > 0 $$

$$ {x}^3 \left(x^2 - 64\right) > 0 $$

$$ {x}^3 \left(x - 8\right)\left(x + 8\right) > 0 $$

Имеем интервалы знакопостоянства:

$$ \left(-\infty;\: -8\right) $$, где \( {x}^3 \left(x - 8\right)\left(x + 8\right) < 0 \) (чтобы узнать, что на этом интервале <0 или, наоборот, >0, можно подставить любое значение \( x < -8 \), например, -10)

\( \left(-8;\: 0\right) \), где \( {x}^3 \left(x - 8\right)\left(x + 8\right) > 0 \)

\( \left(0;\: 8\right) \), где \( {x}^3 \left(x - 8\right)\left(x + 8\right) < 0 \)

\( \left(8;\: +\infty\right) \), где \( {x}^3 \left(x - 8\right)\left(x + 8\right) > 0 \)

 Ответ: при \( -8 < x < 0 \) и \( x > 8 \).

Условная запись ответа объединением множеств: \( x \in (-8;\;0) \cup (+8; +\infty) \)

блин уже 4 раз пишу дана функция: y=-5x+1, определите : 1)x, если y=-1 и -4 2) y, если x=-2 и 0,1 3) возрастающая или убывающая функция? 4) точки пересечения с осями координат. 5)y: наибольшая, y наименьшая на (2, 4)

1)y=-1 -1=-5x+1 -2=-5x x=0.4

    y=-4   -4=-5x+1 -5=-5x x=1

2)x=-2  y=-5*-2+1=11

  x=0.1  y=-5*0.1+1=0.8

3) убывающая

4) пересечение с 0у 0=-5х+1  х=0.2

 пересечение с 0х  y=1

5)y наиб=-5*2+1=-9

 у наим=-5*4+1=-19

1) у=-1 2) х=-2 3) убывающая 4) с 0х

-5х+1=-1 у=10+1=11 у=0

-5х=-2 х=0,1 -5х+1=0

х=2/5=0,4 у=-5,5+1=-4,5 -5х=-1

у=-4 х=0,2

-5х+1=-4 с Оу

-5х=-5 х=0

х=1

5) у наиб. =-5*2+1==9

у наим.=-5*4+1=-19  у=1