график функции »

предел функции

  • Чему равен предел (lim) числа 3 в степени 1-n и почему?


    Решение: Lim3^(1-n)
    Распишем 3^(1-n) =3^1 / 3^n
    Так как, n стремится к бесконечности то получаем, что 3^n бесконечно большое чисто,
    а число 3 делим на бесконечно большое число, значит получаем 0.
    и так Lim0=0 
    ^-степень
    и под lim не забывайте подписывать, что n стремится к бесконечности. 

  • Найти предел, не используя правило Лопиталя: предел дроби (х+3)/(х+4) в степени (-2х), где х стремится к бесконечности
    \( \lim_{x \to \infty} ((x+3)/(x+4))^{-2x} \)


    Решение: $$ \lim_{x \to \infty}( \frac{x+3}{x+4} )^{-2x}= \lim_{x \to \infty}( \frac{x+4-1}{x+4} )^{-2x}= \\ = \lim_{x \to \infty}( 1-\frac{1}{x+4} )^{-2x}=\lim_{x \to \infty}( 1+\frac{1}{-(x+4)} )^{-(x+4) \frac{2x}{x+4} }= \\ =e^{ \lim_{x \to \infty} \frac{2x}{x+4} }=e^{ \lim_{x \to \infty} \frac{2x/x}{x/x+4/x} }=e^2 $$

  • Найти предел lim (n стремится к бесконечности)дробь,в числителе (n+2)во 2 степени, - (n-2) во 2 степени; в знаменателе (n+3) в 2 степени


    Решение:

    Надо упростить дробь
    В числителе (n+2)²-(n-2)²=(n+2 - (n-2) ) ·  (n+2 +n-2)=4·2n
    Знаменатель можно оставить прежним.
    Разделим дробь на n²

    В числителе останется 8/n  - это бесконечно малая величина при n стремящемся к бесконечности. Поэтому в пределе она равна 0
    в Знамнателе (n+3)/n    = 1+3/n
      стремится к 1 при n стремящемся к бесконечности
    ответ 0

  • Найти предел функции НЕ применяя правило Лопиталя: lim x->2 (3х-5)^(2х/(х^2-4))
    (в степени дробь)


    Решение: Соображения такие  limx->2(3x-5)=1  показатель  2x/(x^2-4)=2x/(x(x-4/x))=2/(x-4/x)
    lim(x->2)(2/(x-4/x)=2/0=бесконечности, а 1 в степени ∞ = 1

    Можно воспользоваться таким следствием из второго замечательного предел что 
     $$ lim \\ x->0 \\ \frac{ln(1+x)}{x}=1 $$ 
     Перейдем к нашему пределу 
     $$ x->2 \\ \ (3x-5)^{\frac{2x}{x^2-4}}\\ x->2 \\ \ e^{\frac{ln(3x-5)*2x}{x^2-4}} $$ 
    сделаем теперь некую замену $$ x-2=y $$ , тогда $$ y->0 $$ предел примет вид без основания 
      $$ y->0 \\ \frac{ln(3y+1)*2(y+2)}{y^2-4y}\\ y->0 \\ \frac{ln(3y+1)*4}{3y(\frac{y}{3}+\frac{4}{3})}=\\ y->0 \\ \ 1*\frac{4}{\frac{4}{3}}=3 $$
     то есть предел равен $$ e^3 $$

  • Найти предел. Как быть с третьей степенью в знаменателе? \( lim_{x->-1}\frac{x^2-x-2}{x^3+1} \)


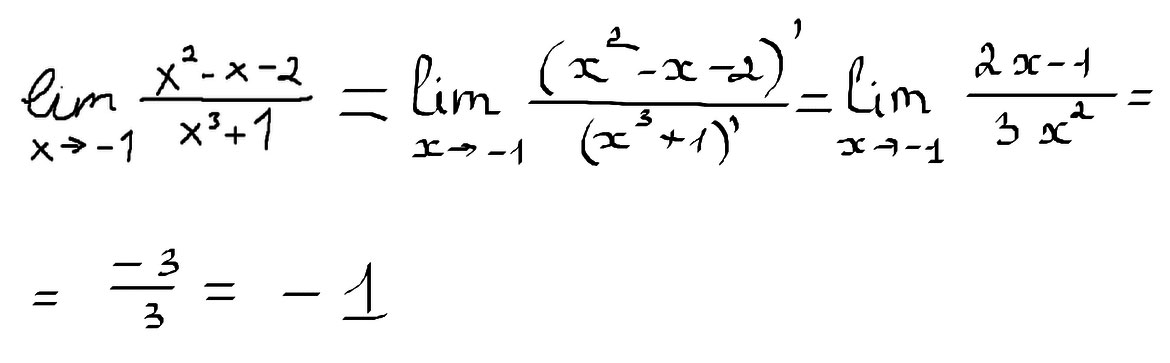
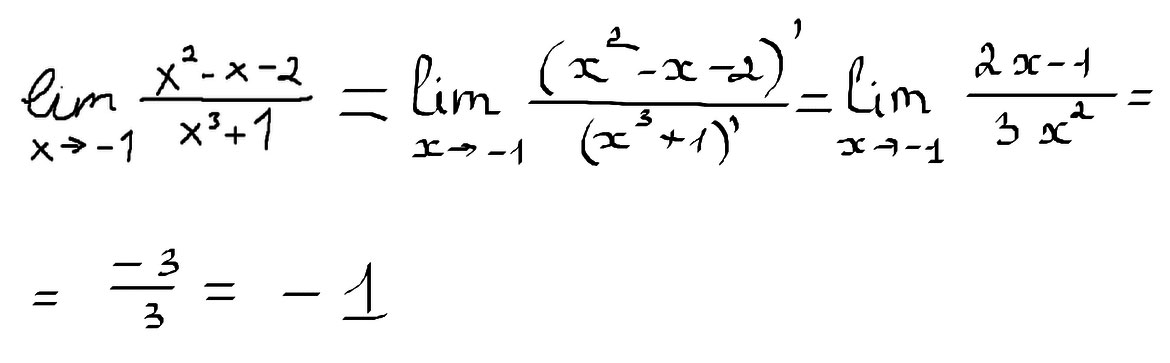
    Решение: Подставив -1 получим неопределенность вида 0/0. Используем правило Лопиталя для вычисления этой границыПодставив - получим неопределенность вида . Используем правило Лопиталя для вычисления этой границы...
1 2 > >>