координаты »
точки на координатной плоскости
Изобразите систему координат Oxyz, и постройте точку А (1;-2;-4). НАЙДИТЕ расстояние от этой точки до координатных плоскостей.
Решение: расстояние от точки А до координатных плоскостей
= 2 до X0Z
= 4 до X0Y
= 1 до Y0Z
СМОТРИ РИСУНОК: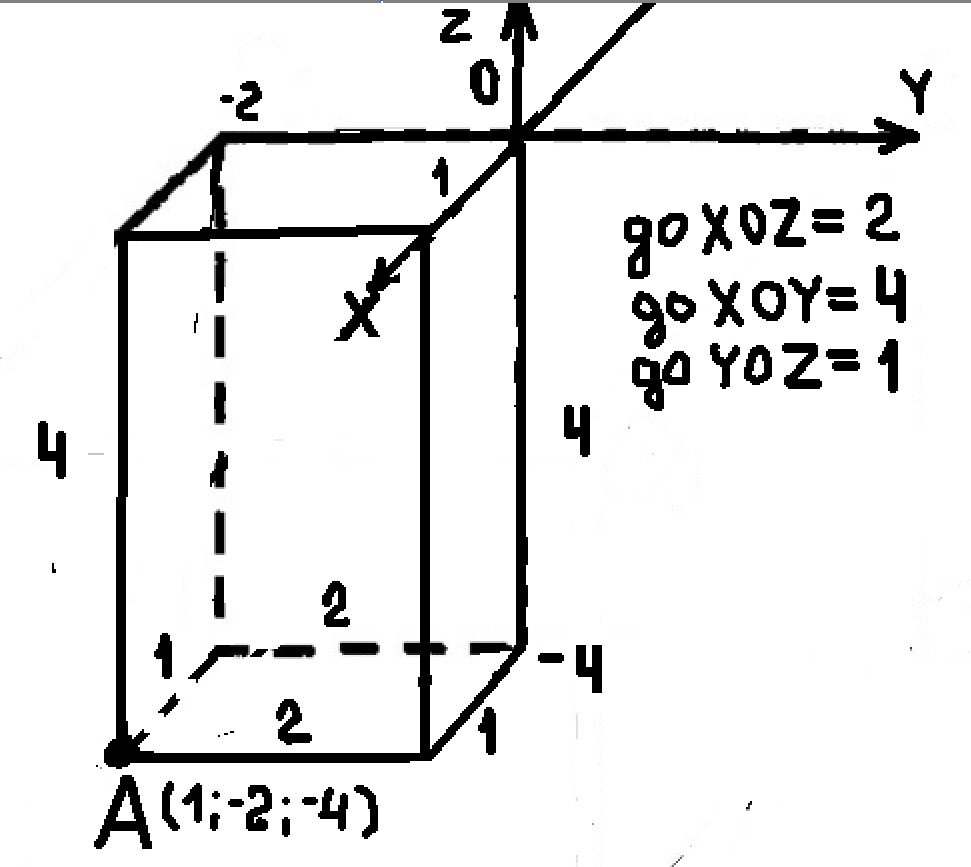
Отметьте и последовательно соедините на координатной плоскости точки, координаты которых приведены в двоичной системе счисления. (101, 101) (101, 101000)
Решение: 1. Координаты первой точки (101;101)
В десятичной системе - (5; 5)
Т.к. 101 = 1×2^2 + 0×2^1 + 1×2^0 = 4+0+1 = 5
2. Координаты второй точки (101; 101000)
Или в десятичной - (5; 40)
101 мы уже вычислили
101000 = 1×2^5 + 0×2^4 + 1×2^3 + 0×2^2 + 0×2^1 + 0×2^0 = 32+0+8+0+0+0 = 40
3. Думаю, нарисовать координатную плоскость и сединить на ней точки (5; 5) и (5; 40) труда не составит.Точка A(a;-3) симметрична точке B(4;b) относительно : a) оси абсцисс; б) оси ординат; в) начало координат. Найдите значения a и b.
Решение: Точка А симметрична точке В относительно оси абсцисс значит справедливы равенства
$$ x_1=x_2;y_1=-y_2 \\ a=4; b=3 $$
-
точка А симметрична точке В относительно оси ординат, значит справедливы равенства
$$ x_1=-x_2;y_1=y_2 \\ a=-4;b=-3 $$
-
точка А симметрична точке В относительно начала координат, значит справедливы равенства
$$ x_1=-x_2;y_1=-y_2 \\ a=-4;b=3 $$
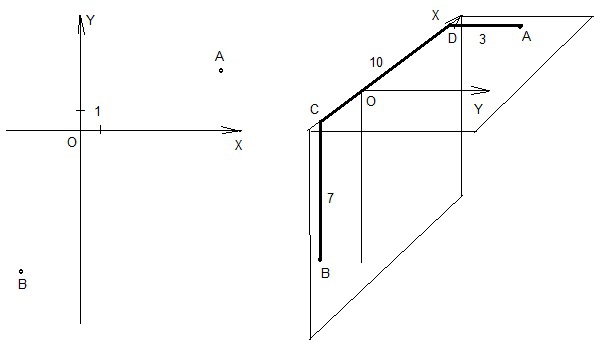
Координатную плоскость перегнули под прямым углом вдоль оси Ох. Найдите расстояние между точками А и В, если на неперегнутой координатной плоскости они имели следующие значения координат: А(7;3) и В (-3;-7).
Решение: Вот слева то, что было, а справа, что стало - перегнули по Ох.
Жирными линиями выделил отрезки вдоль осей.
BD = √(BC^2 + CD^2) = √(7^2 + 10^2) = √(49 + 100) = √149
AB = √(BD^2 + DA^2) = √(149 + 3^2) = √(149 + 9) = √158
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...