координаты »
в одной системе координат построить
В одной системе координат построить графики функций: а) y=1\4x б) y= -4
Решение: Неточность в записи задания приводит к тому, что непонятно, какая функция, собственно, задана формулой у=1/4х, поэтому выкладываю 2 решения: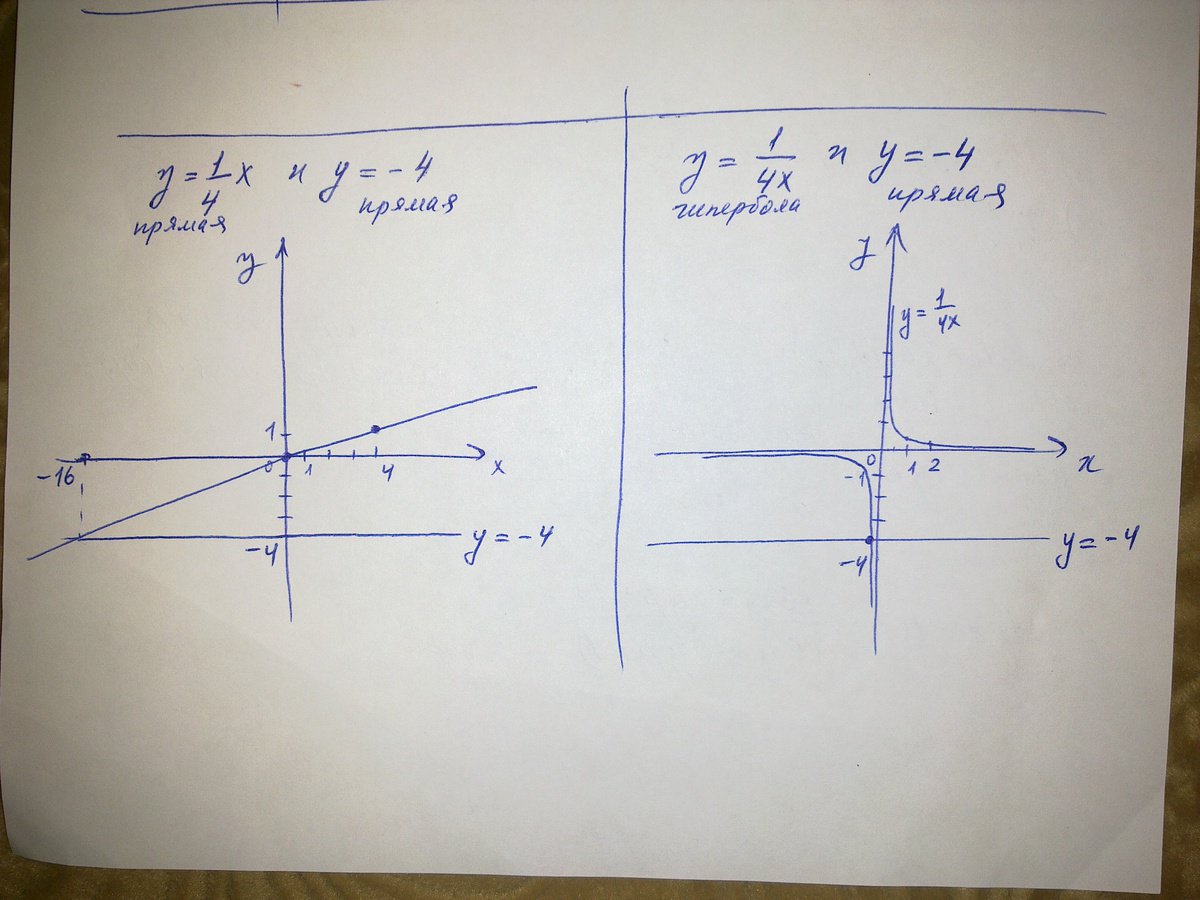
В одной системе координат постройте прямую x-2y=6 и x-2y=-1.объяснить почему эти прямые не имеют общей точки
Решение: Приведем к виду
y = kx +b
k = tg<(y(x),oX)
k - тангенс угла между осью ОХ и линией прямой
если k будут равны, значит прямые параллельны и не имеют общей точки
x-2y=6 ; 2y = x -6 ; y = 1/2 x - 3 ; k = 1/2
x-2y=-1; 2y = x +1 ; y = 1/2 x + 1/2 ; k = 1/2
k = 1/2
прямые параллельны и не имеют общей точки
графики прилагаются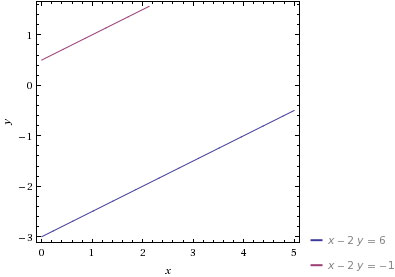
Построить в одной системе координат графики функций y=2x-6; y=-2/3x;y=-1,5
Решение: Графики в приложенных файлах. Чтобы найти координаты подставим в x или y любое число и решим уравнение. Например: y=2x-6, пусть x=2, Тогда y=2*2-6=-2, значит координата точки (2;-2) и т.д. По точкам начертим графики.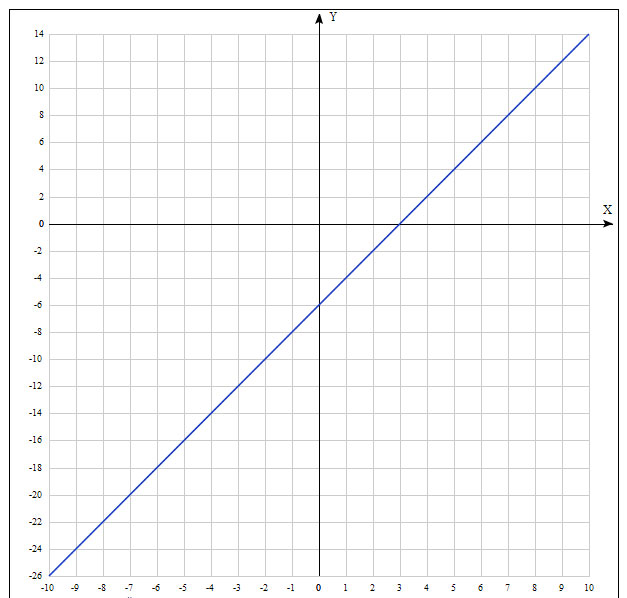
С помощью построенных в одной системе координат графиков функций у=(х) и у=3 решите неравенство:
а) (х)≤ 3; в) х∧3
Решение: Из графиков видно что:
а) $$ |x| \leq 3 $$ это по сути нижняя часть прямой у=|х| которая лежит под графиком у=3, тогда ответ
$$ -3 \leq x \leq 3 $$
б) $$ x<3 $$ это часть прямой у=|х| которая лежит под графиком у=3 с правой стороны и левее до бесконечности, тогда ответ
$$ x<3 $$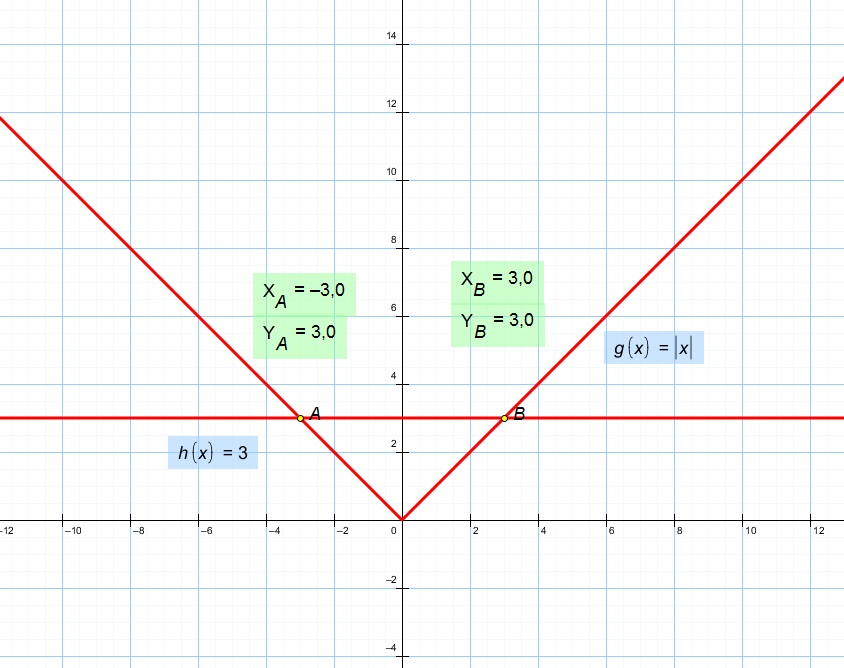
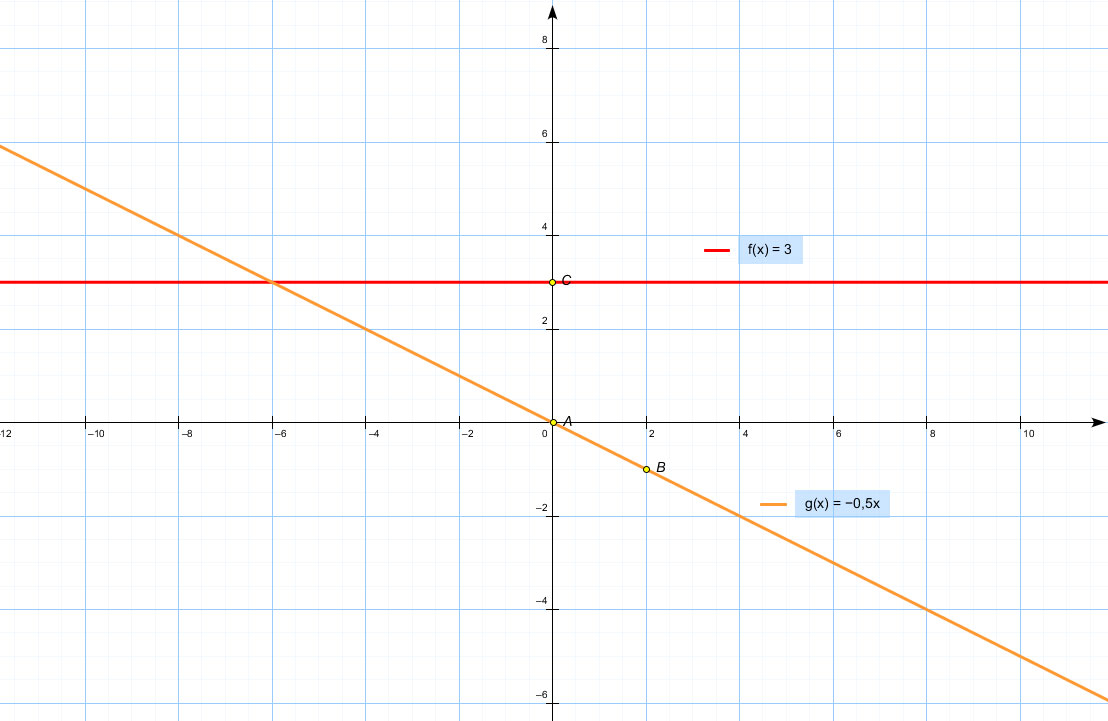
Построить графики функции в одной системе координат
а)у=-0.5x б)y=3
Решение: Это прямые. Достаточно двух точек
а) х | 0 | 2
y | 0 | -1
б) это прямая параллельна оси ОХ и проходит через точку у=3
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...