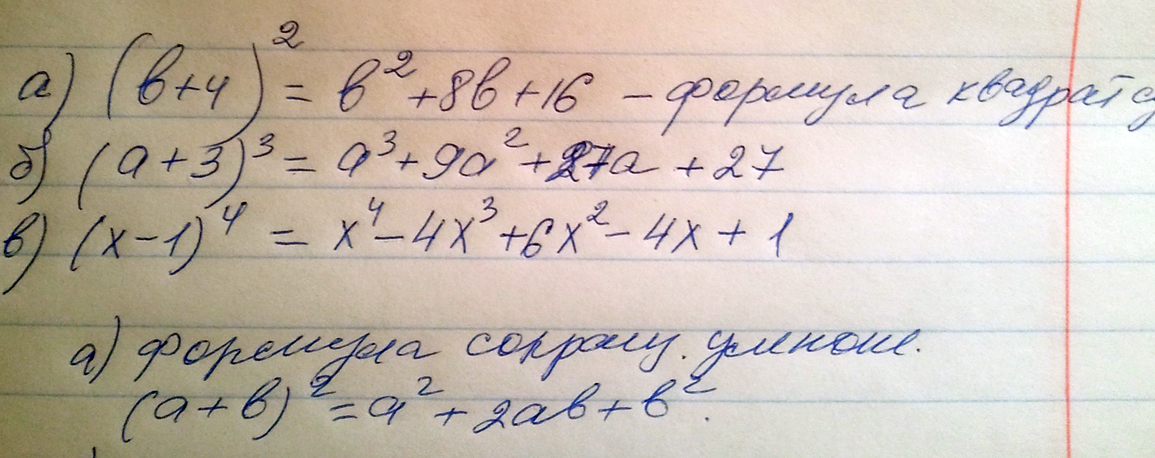многочлен »

произведение многочленов

  • Замените степень произведением и преобразуйте это произведение в многочлен:
    а) (b+4)^2
    б) (a+3)^3
    в) ( x-1)^4


    Решение: $$ (b+4)^2=(b+4)(b+4)=b^2+4b+4b+16=b^2+8b+16, \\ \\ (a+3)^3=(a+3)(a+3)(a+3)=(a^2+3a+3a+9)(a+3)=\\=(a^2+6a+9)(a+3)=a^3+3a^2+6a^2+18a+9a+27=\\=a^3+9a^2+27a+27, \\ \\ \\ (x-1)^4=(x-1)(x-1)(x-1)(x-1)=\\=(x^2-x-x+1)(x^2-x-x+1)=(x^2-2x+1)(x^2-2x+1)=\\=x^4-2x^3+x^2-2x^3+4x^2-2x+x^2-2x+1=\\=x^4-4x^3+6x^2-4x+1. $$

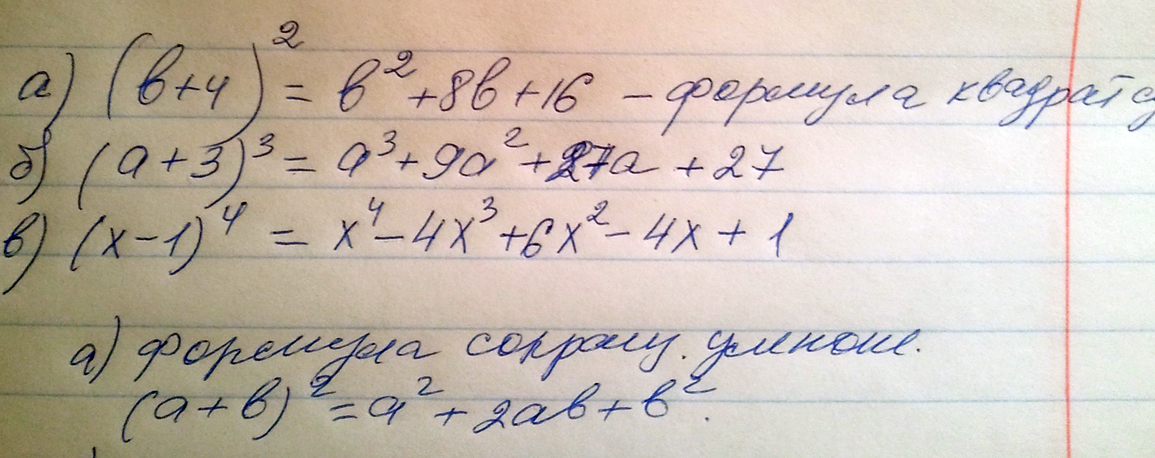
    b b b b b b b b a a a a a a a a a a a a a a a a a a a x- x- x- x- x- x -x-x x -x-x x - x x - x x - x x - x x - x x - x x - x x - x ....

  • Преобразуйте произведение многочленов в многочлен стандартного вида.


    Решение: Просто каждый член каждой скобки умножаете на другие члены в другой скобке. а потом подобные складываете
    1. =(а²+а+а+1)(а+1)=а³+а²+а²+а+а²+а+а+1= (а+1)³ либо а³+3а²+3а+1
    2. =а²+ab+ab+b²(a-b)=a³-a²b+a²b-ab²+a²b-ab²+ab²-b³= а³+а²b-ab²-b³
    3. =a²+ab+ac+a+b+с
    4. =х³-х²+х+х²-х+1= х³+1
    5. =(2х³+4х-6-3х^4-6х²+9х)=(-3х^4+2х³-6х²+13х-6)
    6.= a²+ab-ac+ab+b²-bc+ac+bc-c²=a²+b²-c²+2ab

  • Выполните умножение: б) (12a+b)(3a+5b)
    г) (5m - 2n)(3n - 5m)
    е) (-7x -4y)(-5x+7y)
    Преобразуйте произведение многочленов в многочлен стандартного вида
    а) (8x-3)(4x+5)
    б) 8x-3*4x+5
    в) (4a-3)*2a-3
    г) 4a-3 (2a-3)
    Очень прошу, решите надо(


    Решение: б) (12a+b)(3a+5b)=36а^2+60аb+3аb+5b^2=36a^2+63ab+5b^2;

    г) (5m - 2n)(3n - 5m)=15mn-25m^2-6n^2+10mn=-25m^2+25mn-6n^2;

    е) (-7x -4y)(-5x+7y)=35x^2-49xy+20xy-28y^2= 35x^2-20xy -28y^2;

     а) (8x-3)(4x+5)=32x^2+40x-12x-15= 32x^2+28x-15;

    б) 8x-3*4x+5=8x-12x+5=-4x+5=5-4x;

    в) (4a-3)*2a-3=8a^2-6a-3;

    г) 4a-3 (2a-3)=4a-6a+9=-2a+9=9-2a;

    б) (12а+b)(3a+5b)

    36a в квадрате +60ab +3ab +5b в квадрате

    36 a ы квадрате +63ab + 5b в квадрате

    г) (5m-2n)(3n-5m)

    15mn - 25m в квадрате - 6n в квадрате + 10mn

    - 25m в квадрате + 25mn - 6n в квадрате

    е) (-7x-4y)(-5x+7y)

    35x в квадрате - 49xy +20xy - 28y в квадрате

    35х в квадрате - 29ху - 28н в квадрате

  • Запишите произведение многочленов (1+x)(1+x^2)(1+x^4).(1+x^2048) в стандартном виде


    Решение: Заметим, что степень при x это число 2 в степени i (Уверенно могу это сказать, так как отсутствует (1+x^3)), поэтому произведение будет иметь вид $$ (1+x^{2^{i}} ) $$ где i пробегает от 0 до 11
    2^0 = 1
    2^1 = 2
    2^2 = 4
    2^11 = 2048
    при x = 1 данное произведение будет (1+1).(1+1) = (11 раз) = (1+1)^11 = 2048

  • найдите произведение многочленов 1. (3х+2у)(х-у) 2.(5b-4с)(2b-2c) 3.(p-3q)(8p+5q)


    Решение: 1) 3х в квадрате минус 3ху плюс 2ух минус 2у в квадрате = 3х в квадрате минус ху минус 2у в квадрате
    2) 10b в квадрате минус 10bc минус 8bс плюс 8с в квадрате = 10b в квадрате минус 18bc плюс 8с в квадрате
    3) 8р в квадрате плюс 5рq минус 24рq минус 15q в квадрате = 8р в квадрате минус 19рq минус 15q в квадрате 

    1.(3х+2у)(х-у)=3x*в квадрате*-3xy+2xy-2y*в квадрате*=3x*в квадрате*-xy-2y*в квадрате*

    2.(5b-4с)(2b-2c)=10b*в квадрате*-10bc-8bc+8c*в квадрате*=10b*в квадрате*-2bc+8c*в квадрате*

    3.(p-3q)(8p+5q)=8p*в квадрате*+5pq-24pq-15q*в квадрате*=8p*в квадрате*-19pq-15q*в квадрате*

  • Найти все пары чисел (p, q) чтобы многочлен (картинка) разлагался в произведение многочленов с целыми коэффициентами


    Решение: Для начало если коэффициенты целые, то следует что если мы представим многочлен в виде произведение данных многочленов $$ (x-x’)(ax^4+bx^3+cx^2+dx+e) $$, то число $$ x’ $$ должен быть натуральным делителем, возможен вариант $$ x’=1;-1 $$ что при подстановки отпадает. 
    Рассмотрим вариант 
     $$ (ax^3+bx^2+c)(dx^2+fx+l) $$
      Из данного выражение следует следствия 
     $$ ad=1\\ af+bd=p\\ al+bf=q\\ -(bl+cf)=p\\ cf=1-q\\ cl=1\\\\ $$
     то есть единственный вариант когда 
     $$ a=d=c=l=1\\ b=-1 \ f=1 $$
     То есть $$ p=q=0 $$ 
     

  • №664 Преобразуйте произведение в многочлен
    а)3ab (a^2-2ab+b^2);
    b)-x^2y(x^2y^2-x^2-y^2);
    c)2,5a^2b(4a^2-2ab+0,2b^2);
    d)(-2ax^2+3ax^2-a^2)(-a^2x^2);
    e)(6,3x^3y-3y^2-0,7x)*10x^2y^2;
    f)(-1,4p^2q^6(5p^3q-1,5pq^2-2q^3).


    Решение: а)3ab (a^2-2ab+b^2)=3a³b-6a²b²+3ab³
    b)-x^2y(x^2y^2-x^2-y^2)=-x^4y³+x^4y+x²y³
    c)2,5a^2b(4a^2-2ab+0,2b^2)=10a^4b-5a³b²+0,5a²b³
    d)(-2ax^2+3ax^2-a^2)(-a^2x^2)=2a³x^4-3a³x^4+a^4x²
    e)(6,3x^3y-3y^2-0,7x)*10x^2y^2=63x^5y³-30x²y^4-7x³y²
    f)(-1,4p^2q^6(5p^3q-1,5pq^2-2q^3)=-7p^5q^7+2,1p³q^8+2,8p²q^9

    А) 
    $$ =3a^3b-6a^2b^2+3ab^3 $$
    b)
    $$ =-x^4y^3+x^4y+x^2y^3 $$
    c) 
    $$ = 10a^4b-5a^3b^2+0.5a^2b^3 $$
    d)
    $$ =2a^3x^4-3a^3x^4+a^4x^2 $$
    e)
    $$ =63x^5y^3-30x^2y^4-7x^3y^2 $$
    f) 
    $$ = -7p^5q^7+2.1p^3q^8+2.8p^2q^9 $$