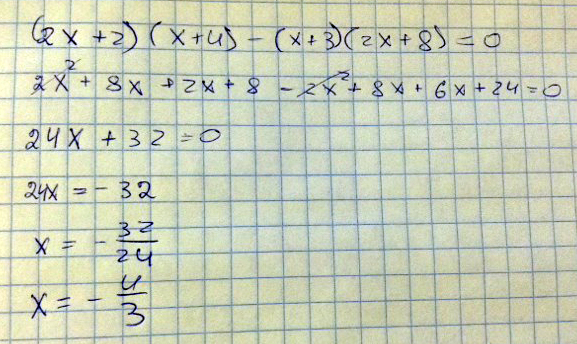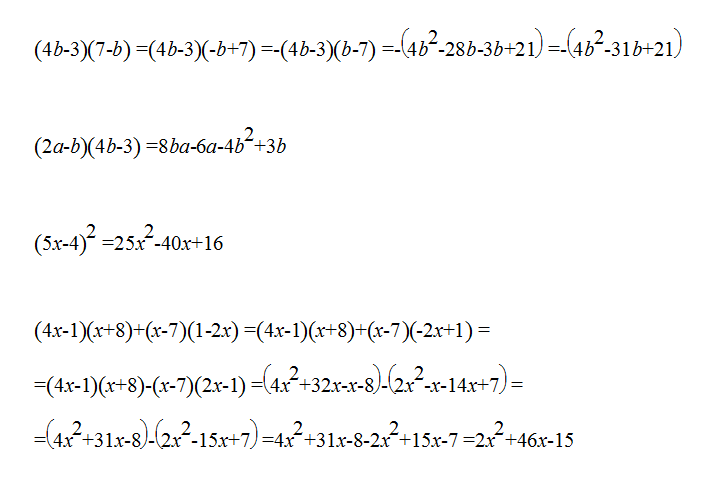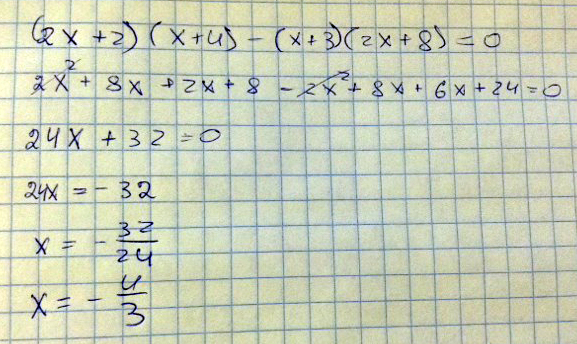многочлен »

умножение/деление многочлена на многочлен

  • Умножение многочлена на многочлен. Вынесение общего множителя за скобки
    1. а)-3х(2х-1);
    б)(2а-b)*8b+8b во второй степени
    2. а)3ах + 4а;
    б)6х во второй степени - 3х.


    Решение: 1. а)-3х(2х-1)=-6x²+3x.

    б)(2а-b)*8b+8b²=16ab-8b²+8b²=16ab.

    2. а)3ах + 4а=2a(1,5x+2).

    б)6x² - 3х=3x(2x-1).

  • Умножение многочлена на многочлен (x-t)*(x^2+2xt-3t^2)


    Решение: рассмотрим 2 множитель  где х-переиенная а t какое-то число
     x^2+2xt-3t^2=0  D=(2t)^2-4*(-3t^2)=4t^2+12t^2=16t^2  VD=+-4t  x1=-2t-4t/2=-3t  x2=-2t+4t/2=t  =>x^2+2xt-3t^2=(x+3t)(x-t)
     запишем твой пример  (x-t)(x-t)(x+3t)=(x-t)^2(x+3t)=x^2-2xt+t^2)(x+3t)=
      x^3-2x^2t+xt^2+3tx^2-6xt^2+3t^3=x^3+x^2t-5xt^2+3t^3
      а можно прямо в лоб перемножать
      (x-t)(x^2+2xt-3t^2)=x^3+2x^2t-3xt^2-x^2t-2xt^2+3t^3=x^3+x^2t-5xt^2+3t^3

  • умножение многочлена на многочлен
    (4в-3)(7-в)
    (2а-в)(4в-3)
    (5х-4) всё это в 2 степени
    (4х-1)(х+8)+(х-7)(1-2х)


    Решение: 1)      (4в-3)(7-в) = 28в-4в²-27+3в

    2)      (2а-в)(4в-3)= 8ав-6а-4в²+3в

    3)      (5х-4)²= 25x² – 40x +16

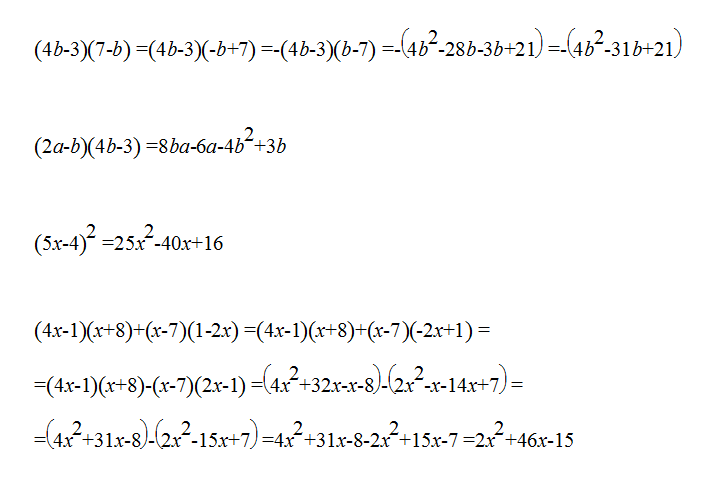
    4)      (4х-1)(х+8)+(х-7)(1-2х) = 4x²+32x–x-8+x-2x²–7+14x = 2x²+45x-15      в- -в в- в - в       а-в в- ав- а- в в       х- x x       х- х х- - х x x x- x- x x x x-...

  • При каких значениях a многочлен F(x)=2x^4+ax^3-9x^2+23x-20 можно разделить на многочлен G(x)=x^2+3x-a ? Желательно при решении воспользоваться теоремой Безу.


    Решение: Согласно теореме Безу остаток от деления полинома на двучлен равен значению полинома в корне этого двучлена, в данной задаче на полином G(x) никаких дополнительных условий не наложено, значит он может быть неприводимым над полем вещественных чисел, однако все равно раскладываться в произведение двучленов вида $$ G(x)=(x-z)(x-\frac{ }{z}) $$

    Где \(\frac{ }{z}\) комплексно сопряжен z.

    Полином G(x) примет вид $$ G(x)=x^2+2Re(z)x+|z| $$

    Re(z)-вещественная часть z,$$ |z|=\sqrt{\frac{9}{4}+\frac{|9+4a|}{4}} $$-модуль числа z.

    Очевидно, что подставляя получившиеся корни в исходный многочлен используя теорему Безу вычисление получается мягко говоря неудобным.

    Аналогичная ситуация со схемой Горнера.

    А вот при делении полиномов столбиком исходный многочлен представим в виде:

    $$ F(x)=G(x)(2x^2+(a-6)x-(a-3))+(-a-3)x^2+(a^2-6a+23)x-20 $$

    Очевидно, что степень остатка должна быть меньше степени делителя и мы можем остаток разделить на полином G(x), домноженный на (-a-3), тогда для того чтобы остаток от деления был равен нулю, то есть чтобы F(x) делился на G(x) должна выполняться система:

    $$ \left \{ {{a^2-6a+23=-3a-9} \atop {a^2+3a=-20}} \right. $$

    Которая не имеет решений ни в поле действительных, ни в поле комплексных чисел.

    Значит ни при каких значениях a полином G(x) не является делителем F(x).

  • Умножение многочлена на многочлен
    (2х+2)(х+4)-(х+3)(2х+8)=0


    Решение: 2х^2+8х+2х+8-2х^2-8х-6х-24=0
    -4х-16=0
    -4х=16
    х=16/-4
    х=-4

    Раскрывая скобки мы получаем 2x^2 и -2x^2 тем самым мы их сокращаем складываем 8x+2x+8x+6x мы получаем 24x и складываем простые числа и получаем 32. Эти 32 мы перенести в право и получаем -32 в следующем действии мы делим -32 на 24 сокращаем и получаем -4/3 х х х - х - х- х- - х- - х х - х - Раскрывая скобки мы получаем x и - x тем самым мы их сокращаем складываем x x x x мы получаем x и складываем простые числа и получаем . Эти...