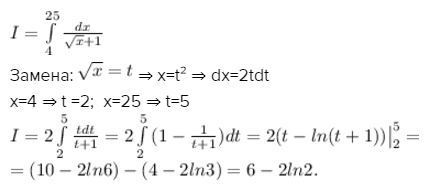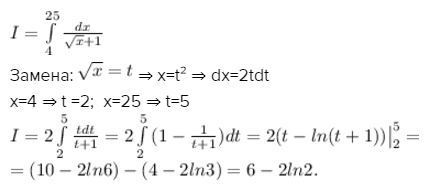интеграл »
найти интеграл методом замены переменной - страница 2
Вычислите определённый интеграл, используя указанную замену переменной \( \int\limits_0^3 \sqrt{9-x^2}dx, \; (x=3sint) \)
Решение: Так как мы имеем случай, где $$ \sqrt{a^2-b^2x^2} $$, используем тригонометрическую подстановку x=a/b sinx
$$ \sqrt{9-(3\sin t)^2} =3 \sqrt{\cos^2t} =3|\cos t| \\ \int\limits^{\arcsin \frac{3\cdot1}{3} }_{\arcsin \frac{0\cdot1}{3} } {3|\cos t|\cdot 3\cos t} \, dt = \int\limits^{ \frac{\pi}{2} }_0 {9\cos^2t} \, dt=9 \int\limits^{\frac{\pi}{2}}_0 { \frac{1+\cos2t}{2} } \, dt=\\ \\=9\cdot0.5( \int\limits^{\frac{\pi}{2}}_0 {1} \, dt + \int\limits^{\frac{\pi}{2}}_0 {\cos2t} \, dt)=9\cdot0.5(1\cdot \frac{\pi}{2}-1\cdot0+0)= \frac{9\pi}{4} $$
Вычислить интегралы: а) методом замены переменной; б) методом интегрирования по частям.
A) S 7x^3dx/5+2x^4
Б) S (2x-3)sin x/2 dx
Решение: $$ \int{ \frac{7x^3dx}{5+2x^4} } \,=[5+2x^4=u;du=8x^3dx]= \\ \\= \frac{7}{8} \int{ \frac{8x^3dx}{5+2x^4} } \, = \frac{7}{8} \int{ \frac{du}{u} } \, =\frac{7}{8} ln|u|+C=\frac{7}{8} ln|5+2x^4|+C \\ u=2x-3 \Rightarrow du=2dx \\ \\ dv=sin \frac{x}{2} dx\Rightarrow v=-2cos \frac{x}{2} \\ \int{(2x-3)sin \frac{x}{2} } \, dx =-2(2x-3)cos \frac{x}{2}- \int{(-cos \frac{x}{2}) } \, 2dx= \\ \\ =(6-4x)cos \frac{x}{2}+2\int{cos \frac{x}{2} } \,dx=(6-4x)cos \frac{x}{2}+4sin\frac{x}{2}+C $$
Заменить переменную в неопределённой интеграле \( \int\limits_{\frac{1}{3}}^{\frac{\sqrt3}{3}}\frac{dx}{\sqrt{4-9x^2}} \)
Решение: Сначала преобразуем наш интеграл так integral(1/2* dx/sqrt(1-(3/2 * x)^2))= 1/2 integral(dx/sqrt(1-(3/2x)^2)) 3/2 *x=t dt=3/2dx dx=2/3dt 1/2integral(2/3* dt/sqrt(1-t^2))=1/3integral(dt/sqrt(1-t^2))=1/3 arcsin t +c=1/3arcsin(3/2*x)+c, дальше применяем ньютона лейбница формулу, там f(b)-f(a)
Решить определенный интеграл с заменой переменной \( \int\limits^{25}_4 { \frac{dx}{ \sqrt{x} +1} } \)
Решение: $$ I= \int\limits^{25}_4 { \frac{dx}{ \sqrt{x} +1} } $$
Замена: $$ \sqrt{x} =t $$ ⇒ x=t² ⇒ dx=2tdt
x=4 ⇒ t =2; x=25 ⇒ t=5
$$ I=2 \int\limits^{5}_2 { \frac{tdt}{ t +1} } =2\int\limits^{5}_2 { (1-\frac{1}{ t +1} } )dt= 2(t-ln(t+1)) \big|^5_2=\\ = (10-2ln6)-(4-2ln3)=6-2ln2. $$