интеграл »
площадь с помощью интеграла - страница 2
Тема: Расчет площадей плоских фигур с помощью определенного интеграла.
Задача: найти площадь фигуры ограниченной линиями
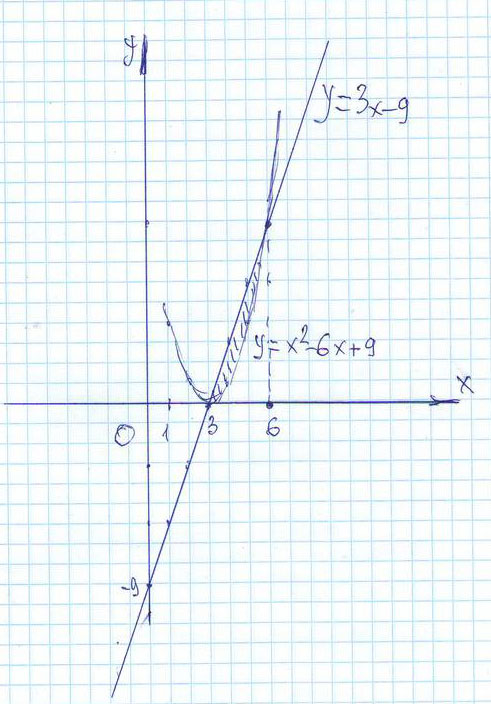
у = x²-6х + 9 у = 3х-9
Решение: У = х² - 6х +9 - это парабола
у = 3х -9 - это прямая.
найдём границы интегрирования. Это точки, которые принадлежат обоим графикам.
х² -6х +9 = 3х - 9
х² - 9х +18 = 0
х = 3 и х = 6 ( по т. Виета
Итак, на участке [3;6] расположена фигура, площадь которой надо искать
Прямая у = 3х -9 выше параболы. Значит, площадь фигуры будем искать так: а) ищем интеграл от (3х - 9)dx, потом б) интеграл от (х² - 6х +9)dx и в) выполним вычитание.
Начали.
а) интеграл от (3х - 9)dx = (3х²/2 - 9х) в пределах от 3 до 6.
считаем: 3·36/2 - 9·6 -(3·9/2-9·3) = 54-54 +27/2 = 13,5
б) интеграл от(х² -6х +9) dx = (х³/3 -6х²/2 +9х) в пределах от 3 до 6.
считаем: получится 9
в) Sфиг = 13,5 - 9 = 4,5