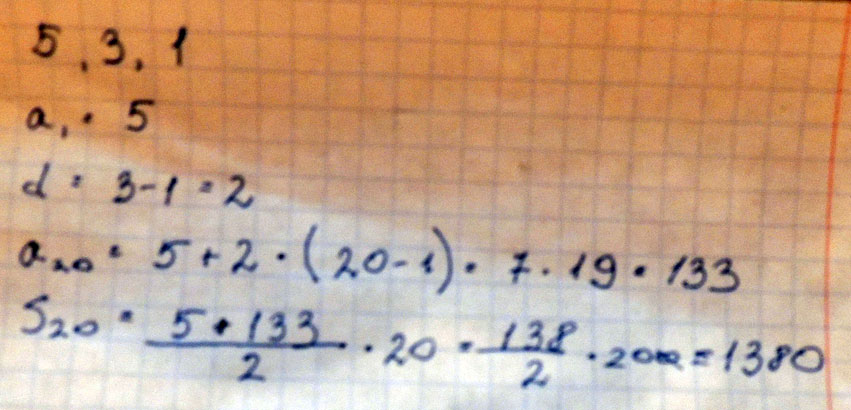прогрессия »

сумма членов арифметической прогрессии - страница 2

  • Дана арифметическая прогрессия an. Вычислите сумму 5 членов, если a9=44 d=4


    Решение: Можно вот так: если d =4, а а9 = 44, то 44-4=40(это а8) 40-4=36(это а7)36-4=32(это а6)32-4=28(это а5) 28-4=24(а4)24-4=20(а3)20-4=16(а2)16-4=12(а1)

    an=a+(n-1)d

    44=a+32

    a=12 (мы нашли a1=12)

    Далее,

    S=n*(a1+an)/2

    S=5*(12+60)/2

    S=60+300/2

    S=360/2

    S=180

    Ответ:180

  • дана арифметическая прогрессия {a^n}Вычислите сумму 7 членов, если A^10=38, d=5


    Решение: а10=38 a9=33 а8=28 а7=23 а6=18 а5=13 а4=8 а3=3 а2=-2 а1=-7

    d=5

    S7- S7= 2*(-7)(7-1)*5

    - *7=56

      2

    Сначала найти $$ a_{1} $$. Т. к. $$ a_{n}= a_{1}+d(n-1) $$, то$$ a_{1}=a_{n}-d(n-1) = a_{10}-d(10-1)=38-5*9= -7. $$
    $$ S_{n}=\frac{(a_{1}+a_{n})n}{2} => S_{7}=\frac{(-7+23)*7}{2} = \frac{112}{2}=56. $$

  • дана арифметическая прогрессия{An}вычислите сумму 9 членов если А15=22 d=1


    Решение: a15=a1+14d

    22=a1+14

    a1=8

     S9=2a1+8d/2 *9=16+8/2*9=12*9=108 

    *Формула нахождения n-го члена арифм. прогрессии:

    an = a1 + d(n-1)

    В данном случае:

    a15 = a1 + 14d

    Подставляем данные числа:

    22 = a1 + 14 * 1

    a1 = 22 - 14

    a1 = 8

    Формула вычисления n членов арифметической прогрессии:

    Sn = ((2*a1 + d(n-1))/2) * n

    В данном случае:

    S9 = (2* 8 + 1*8)/2)*9 = 108

  • Найти сумму первых двенадцати членов арифметической прогрессии 5 3 1


    Решение: найдем разность прогрессии:

    d=3-5 = -2

    а12 = а1 + 11d =5+11*(-2) = 5-22=-17

    S12 = (a1+a12)*12/2 = (5-17)6 = -12*6=-72

    Ответ: S12= -72

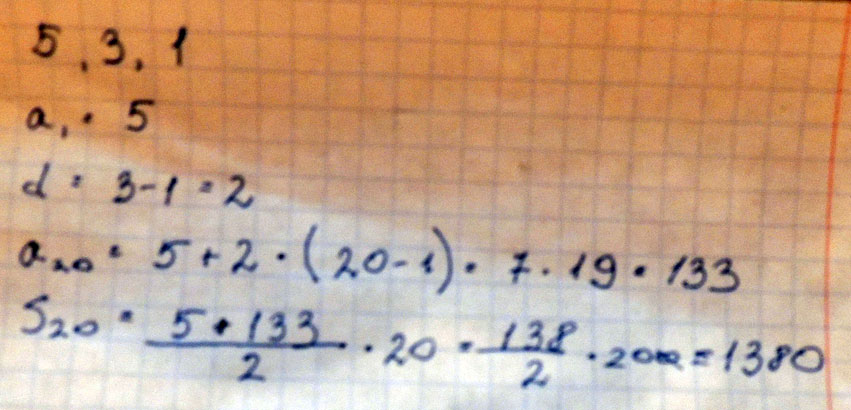
    найдем разность прогрессии d - - а а d - - - S a a - - - Ответ S -...

  • Найти сумму двадцати первых членов арифметической прогрессии (аn), если a5=-0.8, a11=-5


    Решение: Дано: a5=-0.8; a11=-5;
    an=a1 + d(n-1)
    a1 + 10d = -5
    a5=a1 + 4d
    a1 + 4d = -0.8
    решаем систему: a1 + 10d = -5
                                  a1 + 4d = -0.8
    a1 + 10d = -5
    -a1 - 4d = 0.8
    6d = -4.2
    d = -0.7
    a5 = a1 + 4d
    -0.8 = a1 - 2.8
    a1 = 2
    s20 = (a1 + a20)*n/2
    a20 = a1 + 19d= 2 - 13.3= -11.3
    s20= (2 -11.3)*20/2= -9.3*10=-93
    Ответ: -93

    a5=-0.8, a11=-5
    a5=a1+4d
    a11=a1=10d
    -0,8=a1+4d | *(-1)
    -5=a1+10d
    0,8=-a1-4d
    -5=a1+10d
    -4,2=6d
    d=-0,7
    a1+4d=a5
    a1-2,8=-0,8
    a1=2
    S=(2a1+19d)*20/2=2*2+19*(-0,7)*20/2=(4-13,3)*20/1=-9.3*10=-93
    Ответ : -93

<< < 12