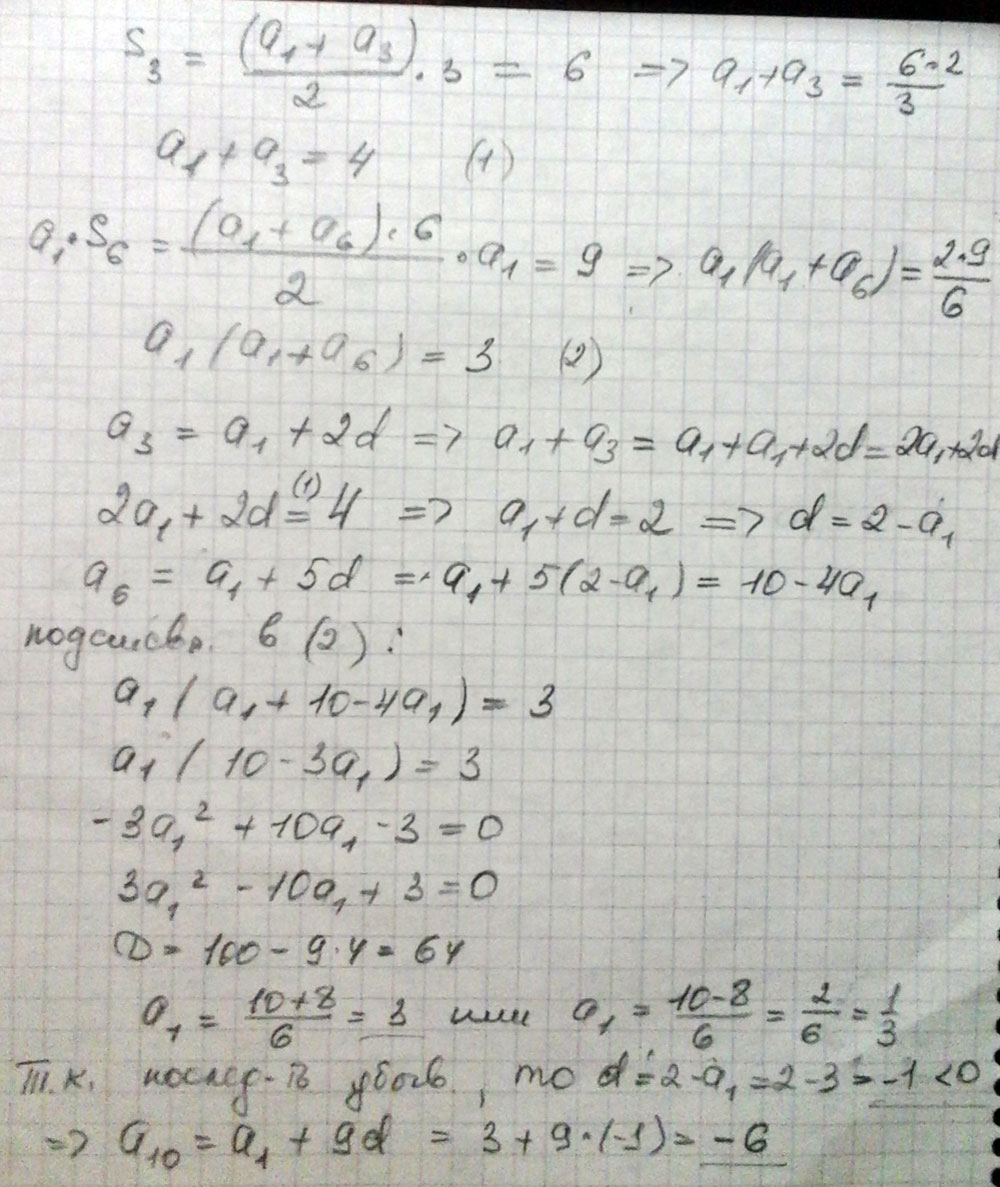прогрессия »

сумма убывающей прогрессии

  • Сумма трех последовательных членов убывающей арифметической прогрессии равна 1, а сумма их трех попарных произведений равна 11/36. Найти эти члены прогрессии. Можно немного поподробней написать решение, а то я мало что понимаю в этой теме.


    Решение: Пусть первый член а1, второй а2, а третий а3. выразим их через формулу n-ого члена. a2=a1+d    a3=a1+2d
    а1+а2+а3=а1+а1+d+a1+2d=3a1+3d=1
    3a1+3d=1
    a1*a2+a1*a3+a2*a3=a1*(a1+d)+a1*(a1+2d)+(a1+d)(a1+2d)=a1^2+a1d+a1^2+2a1d+a1^2+2a1d+a1d+d^2=3a1^2+6a1d+d^2=11/36
    3a1^2+6a1d+2d^2=11/36
    a1=1/3-d
    3(1/3-d)^2+6(1/3-d)d+d^2=11/36
    1/3-2d+3d^2+2d-6d^2+d^2=11/36
    -d^2=11/36-1/3
    d=-1/6
    a1=1/2
    a2=1/3
    a3=1/6

  • Сумма первых трех членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите пятый член прогрессии.


    Решение: a1+a2+a3 = 9

    a12+a22+a32 = 99

    Найти: а5

    Решение:

    a2 = a1+d, a3 = a1+2d

    a1+a1+d+a1+2d = 9                3a1+3d = 9                     a1 = 3-d                       a1 = 3-d

    a12+a22+a32 = 99                     a12+a22+a32 = 99            a12+a22+a32 = 99          (3-d)2+32+(3+d)2 = 99 (2)

    Решим уравнение (2) системы

    (3-d)2+9+(3+d)2 = 99

    9+d2+9+d2 = 90

    18 + 2d2 = 90

    2d2 = 72

    d2 = 36

    d = ± 6

    т. к. (an) – убывающая арифметическая прогрессия, то d = - 6

    а1 = 3+6 = 9

    a5 = a1+4d = 9-24 = -15

    Ответ: а5 = -15

  • Сумма первых трех членов убывающей арифметической прогрессии равна 6, а произведение первого члена на сумму первых шести членов прогрессии равно 9. Найдите десятый член прогрессии.


    Решение:

    Пусть убывающая арифм. прогрессия есть $$ (a_n):\ a_1;\ a_2;\ a_3;. $$
    $$ a_1+a_2+a_3=6\ u\ S_6*a_1=9 $$
    $$ \begin{cases} a_1+a_1+d+a_1+2d=6 \\ \frac{2a_1+5d}{2}*6*a_1=9 \end{cases} \Leftrightarrow \begin{cases} a_1+a_1+d+a_1+2d=6 \\ \frac{2a_1+5d}{2}*6*a_1=9 \end{cases}\\ \Leftrightarrow \begin{cases} a_1+d=2 \\ (2a_1+5d)*a_1=3 \end{cases} \Leftrightarrow \begin{cases} a_1=2-d \\ (4-2d+5d)*(2-d)=3 \end{cases} $$
    3d² - 2d - 5 = 0
    d = -1 или d = 5/3
    Т. к. прогрессия убывающая, то d = -1 ⇒ $$ a_1=2-(-1)=3 $$
    $$ a_{10}=a_1+9d=3+9*(-1)=-6 $$
    Ответ: -6.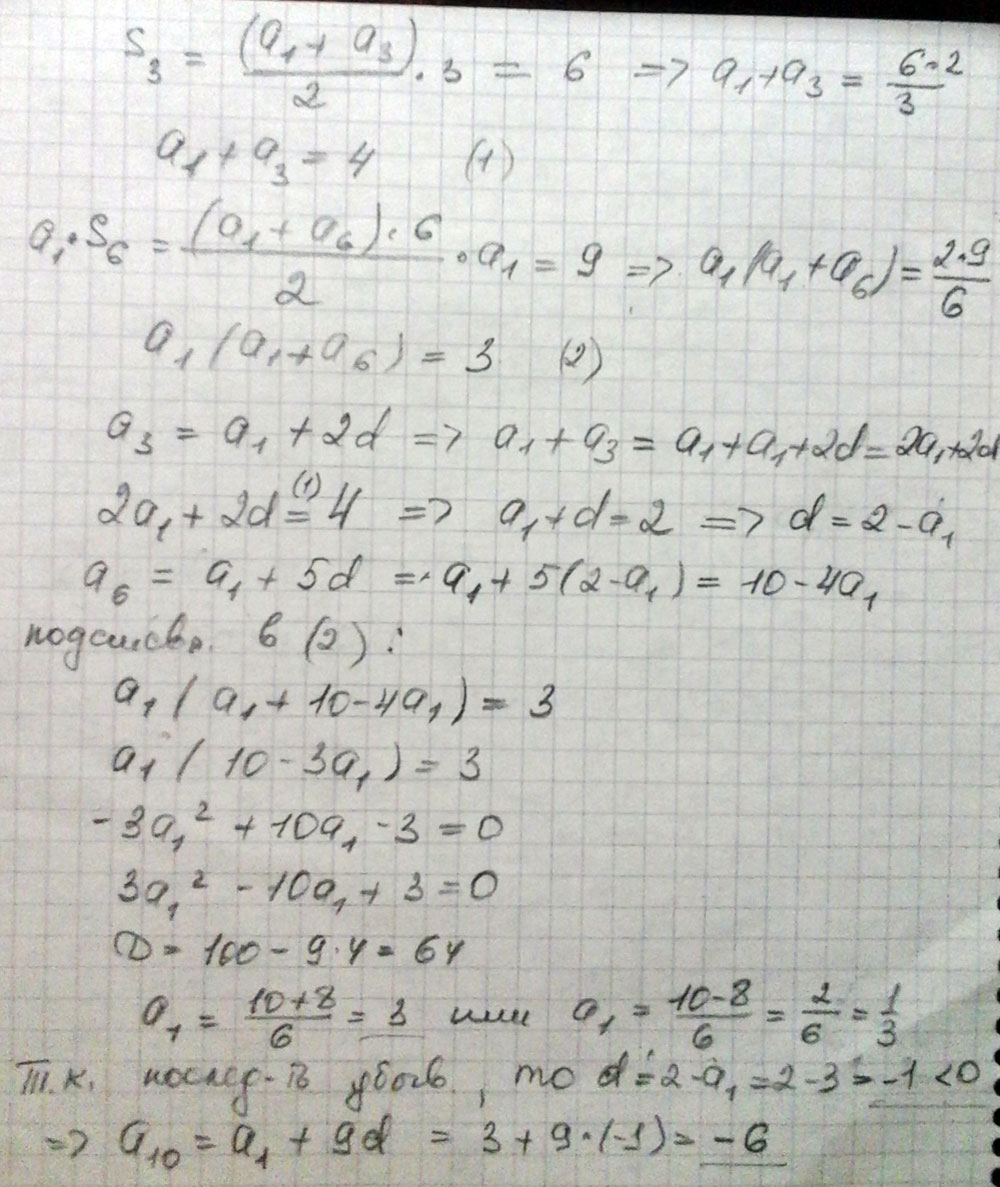

    Пусть убывающая арифм. прогрессия есть  a n a a a . a a a u S a begin cases a a d a d frac a d a end cases Leftrightarrow begin cases a a d a d frac a d a end cases Leftright...

  • Сумма первых трех членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите пятый член прогрессии


    Решение: a₁+a₂+a₃=9;

    (a₁)²+(a₂)²+(a₃)²=99;

    a₁+a₁+d+a₁+2d=9;

    (a₁)²+(a₁+d)²+(a₁+2d)²=99;

    a₁=3-d;

    9-6d+d²+9+9+6d+d²=99;

    a₁=3-d;

    2d²=72;

    a₁=3-d;

    d²=36;

    a₁=9;

    d=-6.

    a₅=a₁+4d=9-24=-15.

    Ответ: а₅=-15.

  • Найти отношение третьего члена убывающей геометрической прогрессии к её пятнадцатому члену, если сумма двенадцати членов прогрессии, начиная с тринадцатого, составляет 2/5 суммы её первых двенадцати членов.


    Решение: Сумма 12-ти членов прогрессии, начиная с 13-ого - это сумма с 13-го по 24-ой член прогрессии: $$ S= \frac{b_{13}}{1-q}=\frac{2}{5}*S_{12} $$
    Сумма первых 12-ти членов: $$ S_{12}= \frac{b_{1}}{1-q} $$
    $$ \frac{b_{13}}{1-q}=\frac{2}{5}* \frac{b_{1}}{1-q} $$
    $$ b_{15}=b_{1}*q^{14} $$
    $$ b_{13}=b_{1}*q^{12} $$
    $$ b_{3}=b_{1}*q^{2} $$
    $$ \frac{b_{1}*q^{12}}{1-q}=\frac{2b_{1}}{5(1-q)} $$
    $$ q^{12}=\frac{2}{5} $$
    $$ \frac{b_{3}}{b_{15}}= \frac{b_{1}*q^{2}}{b_{1}*q^{14}}=\frac{1}{q^{12}}=\frac{1}{\frac{2}{5}}=\frac{5}{2} $$

    Пусть bn- n-ый член прогрессии

    Sn -сумма первых n членов, тогда

    b3=b* q^2

    b15=b*q^14

    b3/b15=(b*q^2)/(b*q^14)=1/q^12

    S12=(b*(1-q^12))/(1-q)

    S24=(b*q^n*(1-q^12))/(1-q)

    S24/Sn=q^12

    b3/b15=Sn/S4=5/2

    ответ 5/2