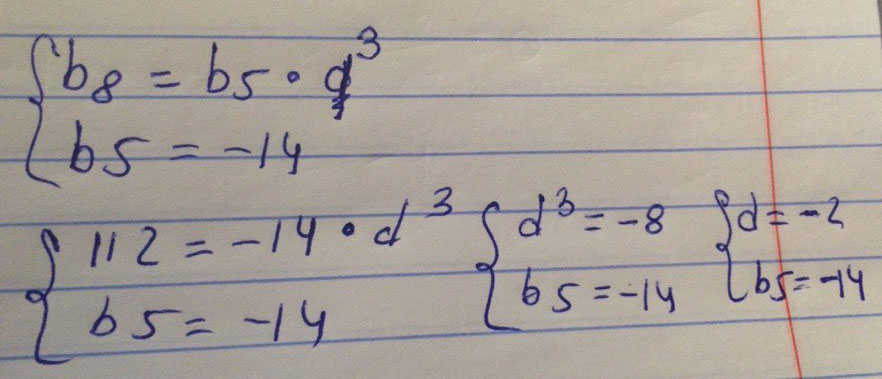прогрессия »

знаменатель прогрессии - страница 2

  • (Bn) геометрическая прогремсия b5=4 b9=1/4 найти знаменатель прогрессии


    Решение: Воспользуемся такими правилами для решения
    b(n) =b1*q^(n-1)
    a^m / a^n = a^(m-n)
    тогда решаем следующим способом
    b5=4
    b9=1\4
    q-
    Применим формулу b(n) =b1*q^(n-1) и получим систему вида
    b5=b1*q^(5-1)
    b9=b1*q^(9-1)
    тогда
    b1*q^4=4
    b1*q^8=1\4
    далее решаем так
    b1=4\q^4
    4\q^4*q^8=1\4
    4*q^8\q^4=1\4
    Теперь используем формулу a^m / a^n = a^(m-n) и получаем
    4*q^(8-4)=1\4
    4*q^4=1\4
    q^4=(1\4)\4
    q^4=0,0625
    q=корень 4й степени из (0,0625)
    q1=1\2
    q2=-1\2
    Ответ - (q1=1\2; q2=-1\2)

  • Дана геометрическая прогрессия (Bn), b которой b3=12,b6=-96. Найдите знаменатель прогрессии


    Решение: Записываем формулу п-го члена геометрической прогрессии
    bn=b1*g в степени(n-1)
    Запишем это для 3 и 6 членов
    b3=b1*g в 2
    b6=b1*g в 5
    из этих уравнений выразим b1
    b1=b3(g в2)
    b1=b6/(g в5)
    получили уравнение, которое раскрываем пропорцией
    12/(g в2)=-96/(g в5)
    12*(g в5)=-96*(g в2)
    12*(g в5)+96*(g в2)=0
    (g в2)((g в3)+8)=0
    (g в2)=0 или (g в3)+8=0
    g=0 (g в3)=-8
      g=-2
    Ответ: g=-2 

  • Дана геометрическая прогрессия (bn), для которой b5=-14, b8=112. Найдите знаменатель прогрессии.


    Решение: Формула: q = bn+1/bn;
    В нашем случае:
    b8 = b5*q^3, выразим отсюда q^3;
    q^3 = b8/b5 = 112/-14 = -8;
    -8 - это знаменатель в третьей степени, значит, q = -2.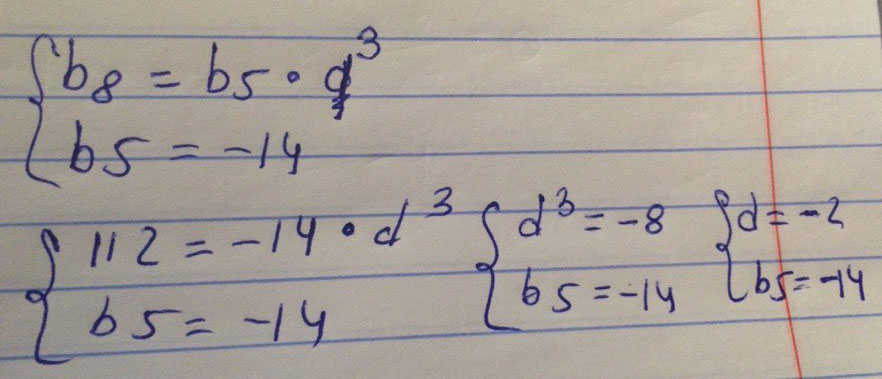

    Формула q bn bn В нашем случае b b q выразим отсюда q q b b - - - - это знаменатель в третьей степени значит q - ....

  • №1.Значение какого из выражений является иррациональным?

    1)\(\sqrt{18}*\sqrt{2}\)

    2)\((\sqrt{12}-\sqrt{23})*(\sqrt{12}+\sqrt{23})\)

    3)\(\frac{12}{27}\)

    4)\(\sqrt{20} +2\sqrt{5}\)

    №2. Решите уравнение.

    \(\frac{x-9}{x-6}=\frac{3}{4}\)

    №3. В геометрической прогрессии \((b_{n}) b_{2}= -0,2, b_{5}=-25\)

    Найдите знаменатель прогрессии.

    №4. Найдите значение выражения

    \((\frac{u}{v}+\frac{v}{u}+2)*\frac{uv}{v+u} при v=3\sqrt{2}+1, u= 4-3\sqrt{2}\)


    Решение: 1)\(\sqrt{18}*\sqrt{2} = √18 * √2 = √(9 * 3) * √2 = 3√2 * √2 = 3 * 2 = 6 \) - не является иррациональным

    2) \((\sqrt{12}-\sqrt{23})*(\sqrt{12}+\sqrt{23}) = (√12 - √23)(√12 + √23) = √12² - √23² = 12 - 23 = -11\) - не является иррациональным

    3) \(\frac{12}{27} = \frac{4}{9}= 0,4\) - является иррациональным

    4)$$ \sqrt{20} +2\sqrt{5} = \sqrt{20} +2\sqrt{5}=\sqrt{4*5} +2\sqrt{5} = 2\sqrt{5} +2\sqrt{5}= 4\sqrt{5}\approx 8,94 $$ - является иррациональным

    $$ \frac{x-9}{x-6}=\frac{3}{4}, \ \ \ xeq6\\ \\ 4*(x-9)=3*(x-6)\\ \\ 4x-36-3x+18=0\\ x-18=0\\ x=18 \\ (\frac{u}{v}+\frac{v}{u}+2)*\frac{uv}{v+u} = (\frac{u^2+v^2+2uv}{vu})*\frac{uv}{v+u} = \frac{(v+u)^2}{v+u} = v+u\\ v+u = 3\sqrt{2}+1+4-3\sqrt{2} = 5 $$

<< < 12