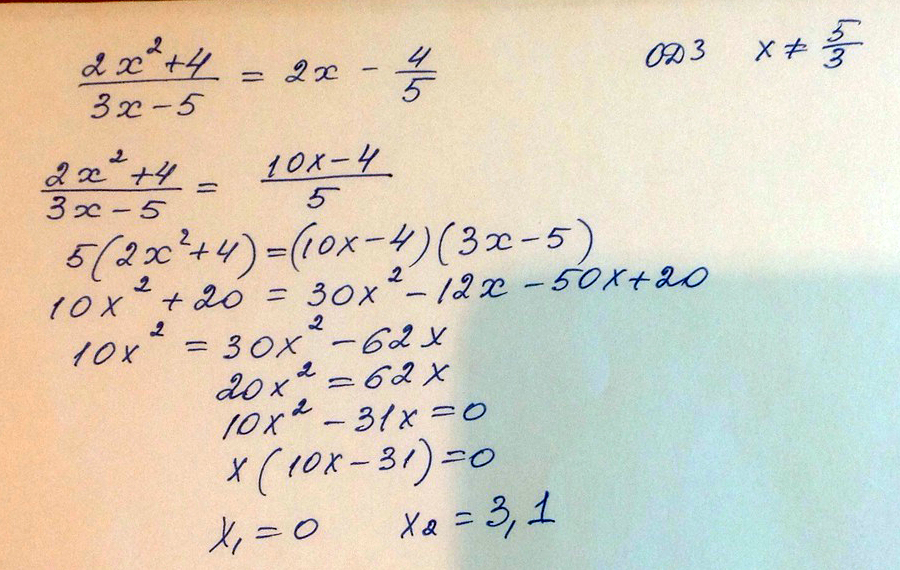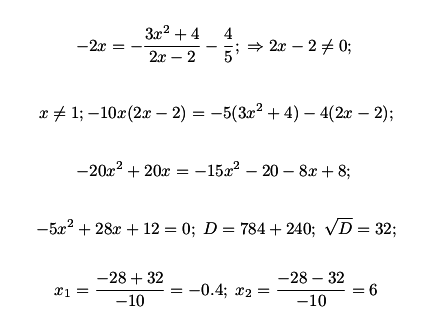решение уравнений »

решение дробных рациональных уравнений

  • Решение дробных рациональных уравнений \(\frac{2x^2+4}{3x-5}=2x-\frac{4}{5}\)


    Решение: Общий знаменатель 5(3x-5)
    5(2x^2+4)=2x*5(3x-5)-4(3x-5)
    10x^2+20=10x(3x-5)-12x+20
    10x^2+20=30x^2-50x-12x+20
    10x^2-30x^2+50x+12x+20-20=0
    -20x^2+62x=0
    x(-20x+62)=0

    x=0
    -20x+62=0
    -20x=-62
    x=3.1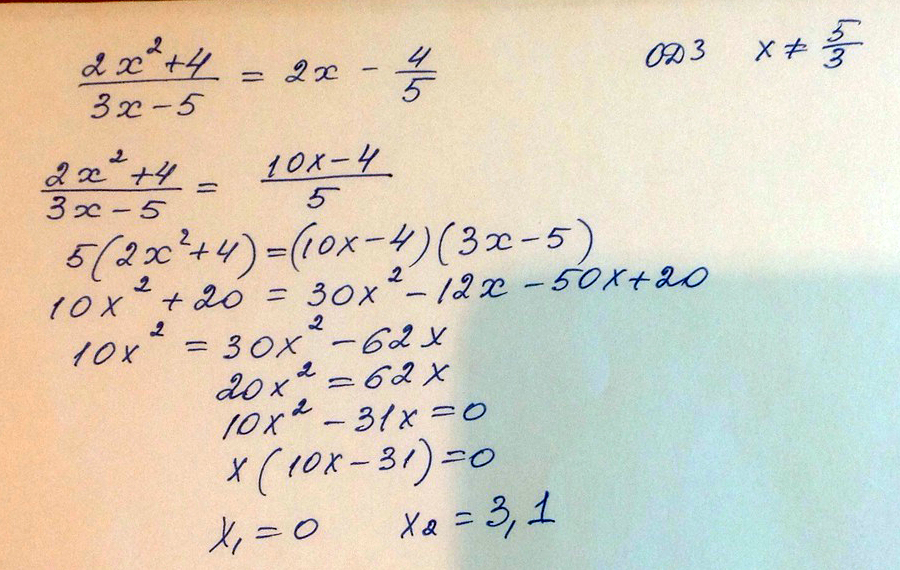

    Общий знаменатель x- x x x- - x- x x x- - x x x - x- x x - x x x - - x x x - x x - x - x - x ....

  • Решение дробных рациональных уравнений \(-2x= -\frac{3x^2+4}{2x-2} -\frac{4}{5}\)


    Решение: $$ \frac{2x*10(x-1)-15x^2-20-8x+8}{10(x-1)} =0\\ x = 1\\ 20x^2-20x-15x^2-20-8x+8=0\\ 5x^2-28x-12=0\\ D=784+240=1024\\ x_1=(28+32):10=6\\ x_2=(28-32):10=-0.4 $$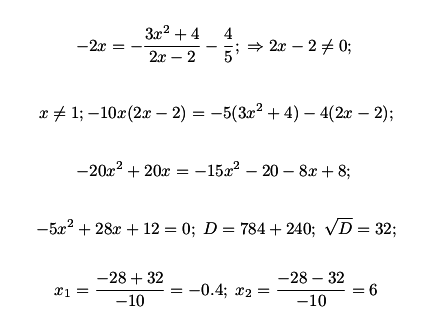frac x x- - x - - x x- x x - x- x - - x x - x- D x x - - ....

  • Сплав золота и серебра содержал 18г золота. Добавив 32г золота, получили новый сплав, с концентрацией золота на 25 процентов выше. Сколько г серебра было в сплаве?


    Решение: Решение

    Пусть в сплаве было Х г серебра, тогда
     
      I сплав II сплав
    __________________________________________________
    вес серебра (г) Х Х
    __________________________________________________
    вес золота (г) 18 18+32=50
    __________________________________________________
    вес сплава (г) Х + 18 Х + 50
    __________________________________________________
    % золота 18/(Х + 18) *100 50/(Х + 50) *100 
    __________________________________________________
    по условию концентрация золота во II сплаве выше на 25 % =>
    $$ \frac{50}{x+50} *100 - \frac{18}{x+18} *100 = 25 \\ $$
    делим обе части на 25
    $$ \frac{50}{x+50} *4 - \frac{18}{x+18} *4 = 1 \\ \frac{200}{x+50} - \frac{72}{x+18} = 1 \\ 200(x+18) - 72(x+50) = (x+18) (x+50) \\ 200x + 3600 - 72x - 3600 = x^{2} + 68x+900 \\ \\ 200x + 3600 - 72x - 3600 = x^{2} + 68x+900 \\ x^{2} - 60x+900=0 \\ D=3600 - 4*900 = 3600 - 3600 = 0 \\ x = \frac{60}{2} = 30 \\ $$
    Ответ: серебра в сплаве 30 г

    Решение Пусть в сплаве было Х г серебра тогда     I сплав II сплав вес серебра г Х Х вес золота г вес сплава г Х Х золота Х Х   по условию концентрация золота во II сплаве вы...

  • Решение дробных рациональных уравнений \(-2x+\frac{5x^2+5}{3+3x}= -\frac{5}{6}\)


    Решение: (-2х(3+3х)+5х^2+5)/(3+3х)=-5/6
    (-6х-6х^2+5х^2+5)/(3+3х)=-5/6
    (-х^2-6х+5)/3(1+х)=-5/6
    (х^2+6х-5)/-3(1+х)=-5/6
    (х^2+6х-5)/(1+х)=5/2
    2(х^2+6х-5)=5(1+х)
    2х^2+12х-10=5+5х
    2х^2+12х-10-5-5х=0
    2х^2+7х-15=0
    д=49-4×2×(-15)=169
    х1=(-7-13)/2×2=-5
    х2=(-7+13)/2×2=3/2=1.5

    Решение состоит из 36 шагов.
    1) Умножаем обе стороны уравнения на $$ 6*(3+3x) $$.
    $$ 6*(3+3x)*-2x+6*(3+3x)* \frac{5 x^{2} +5}{3+3x} = 6*(3+3x)*( -\frac{5}{6} ) $$
    2) Сокращаем дробь путем деления числителя и знаменателя на 3+3x.
    $$ 6*(3+3x)*-2x+6*(5 x^{2} +5)=6*(3+3x)*(- \frac{5}{6} ) $$
    3) Сокращаем дробь путем деления числителя и знаменателя на 6.
    $$ 6*(3+3x)*-2x+6*( 5 x^{2}+5)=-5*(3+3x). $$
    4) Перемножаем значения.
    $$ -12x*(3+3x)+6*( 5x^{2} +5)=-5*(3+3x) $$
    5) Перемножаем значения.
    $$ -12x*(3+3x)+6* 5x^{2} +6*5=-5*(3+3x) $$
    6) Перемножаем значения.
    $$ -12x*(3+3x)+ 30x^{2} +6*5=-5*(3+3x) $$
    7) Перемножаем значения.
    $$ -12x*(3+3x)+30 x^{2} + 30=-5*(3+3x) $$
    8) Перемножаем значения.
    $$ -12x*(3+3x)+30 x^{2} +30=-5*3-5*3x $$
    9) Перемножаем значения.
    $$ -12x*(3+3x)+30 x^{2} +30=-15-5*3x $$
    10) Перемножаем значения.
    $$ -12x*(3+3x)+30 x^{2} +30=-15-15x $$
    11) Перегруппировываем значения.
    $$ -12x*(3+3x)+30 x^{2} +15x=-15-30 $$
    12) Вычисляем разность.
    $$ -12x*(3+3x)+30 x^{2} +15x=-45 $$
    13) Умножаем значения в скобках.
    $$ -12x*3-12x*3x+30 x^{2} +15x=-45 $$
    14) Перемножаем значения.
    $$ -36x-12x*3x+30 x^{2} +15x=-45 $$
    15) Перемножаем значения.
    $$ -36x-36x*x+30 x^{2} +15x=-45 $$
    16) Перемножаем значения.
    $$ -36x-36 x^{1+1} +30 x^{2} +15x=-45 $$
    17) Вычисляем сумму.
    $$ -36x-36 x^{2} +30 x^{2} +15x=-45 $$
    18) Вычисляем сумму.
    $$ -21x-36 x^{2} +30 x^{2} =-45 $$
    19) Вычисляем сумму.
    $$ -21x-6 x^{2} =-45 $$
    20) Переставляем значения.
    $$ -6 x^{2} -21x=-45 $$
    21) Делим обе стороны уравнения на -3.
    $$ \frac{ -6x^{2} }{-3} - \frac{21x}{-3} = \frac{-45}{-3} $$
    22) Сокращаем дробь путем деления числителя и знаменателя на -3.
    $$ 2x^{2} - \frac{21x}{-3} = \frac{-45}{-3} $$
    23) Сокращаем дробь путем деления числителя и знаменателя на -3.
    $$ 2 x^{2} +7x= \frac{-45}{-3} $$
    24) Сокращаем дробь путем деления числителя и знаменателя на -3.
    $$ 2 x^{2} +7x=15 $$
    25) Решаем квадратное уравнения, используя формулу $$ x= \frac{-b \frac{+}{-} \sqrt{ b^{2} -4ac} }{2a} \\ x= \frac{-7 \frac{+}{-} \sqrt{ 7^{2} -4*2*-15} }{2*2} $$
    26) Вычисляем степень.
    $$ x= \frac{-7 \frac{+}{-} \sqrt{49 - 4*2*-15} }{2*2} $$
    27) Перемножаем значения.
    $$ x= \frac{-7 \frac{+}{-} \sqrt{49-8*-15} }{2*2} $$
    28) Перемножаем значения.
    $$ x= \frac{-7 \frac{+}{-} \sqrt{49+120} }{2*2} $$
    29) Вычисляем сумму.
    $$ x= \frac{-7 \frac{+}{-} \sqrt{169} }{2*2} $$
    30) Вычисляем корень.
    $$ x= \frac{-7 \frac{+}{-} 13}{2*2} $$
    31) Перемножаем значения.
    $$ x= \frac{-7 \frac{+}{-} 13 }{4} $$
    32) Находим два решения квадратного уравнения.
    $$ \left \{ {{x= \frac{-7+13}{4} } \atop {x= \frac{-7-13}{4} }} \right. $$
    33) Вычисляем сумму.
    $$ \left \{ {{x= \frac{6}{4} } \atop {x= \frac{-7-13}{4} }} \right. $$
    34) Сокращаем дробь путем деления числителя и знаменателя на 2.
    $$ \left \{ {{x= \frac{3}{2} } \atop {x= \frac{-7-13}{4} }} \right. $$
    35) Вычисляем разность.
    $$ \left \{ {{x= \frac{3}{2} } \atop {x= \frac{-20}{4} }} \right. $$
    36) Сокращаем дробь путем деления числителя и знаменателя на 4.
    $$ \left \{ {{x= \frac{3}{2} } \atop {x=-5}} \right. $$
    Находим общие значения.
    Итог
    $$ x\in {-5, \frac{3}{2}} $$
    или
    x∈ {-5, 1.5}

  • Решение дробных рациональных уравнений \(\frac{5x^2+2}{2x+5}-2x = \frac{2}{5}\)


    Решение: Приводим к общему знаменателю и решим:
    (5x² + 2 - 4x² - 10x) / (2x + 5) = 2 / 5
    (x² - 10x + 2) / (2x + 5) = 2/ 5
    5( x² - 10x + 2) = 2( 2x + 5)
    5x² - 50x + 10 = 4x + 10
    5x² - 50x - 4x + 10 - 10 = 0
    5x² - 54x = 0
    5x(x - 10,8) = 0
    Произведение равно 0, когда один из множителей равен 0, значит,
    5x = 0
    x = 0
    x - 10,8 = 0
    x = 10,8
    Ответ: x = 0. x = 10,8.

  • Решение дробных рациональных уравнений \(\frac{5x^2-4}{2x-1}-2x = \frac{4}{5}\)


    Решение: ОДЗ
    $$ 2x-1=0\\2x=1\\x=\frac{1}{2} $$
    Решение
    $$ 5x^2-4-2x(2x-1)=0.8(2x-1) \\ 5x^2-4-4x^2+2x=1.6x-0.8 \\ x^2+2x-4=1.6x-0.8\\x^2+2x-1.6x-4+0.8=0\\x^2+0.4x-3.2=0\\10x^2+4x+32=0\\5x^2+2x-16=0 \\ D=b^2-4ac=2^2-4*5*(-16)=4-(-320)=324\\x_1=\frac{-b+\sqrt D}{2a}=\frac{-2+\sqrt{324}}{2*5}=\frac{-2+18}{10}=\frac{16}{10}=1.6 \\ x_2=\frac{-b-\sqrt D}{2a}=\frac{-2-18}{10}=\frac{-20}{10}=-2 \\ x_1\in $$ОДЗ; $$ x_2\in $$ОДЗ
    Ответ: $$ x_1=1.6; x_2=-2 $$

    1. домножим обе части на 5(2х-1), что бы убрать знаменатель и получим:
    5(5х ²-4)-2х*5(2х-1)=(2х-1)*4
    2раскроем скобки и упростим :
    5х ²+2х-16=0
    1х=-2
    2х=1,6

  • Решение дробных рациональных уравнений \(\frac{4x^2-4}{3x-5}=\frac{4}{5}+2x\)


    Решение: $$ \frac{4 x^{2} -4}{3x-5} =\\= \frac{4}{5} +2x \\ 4\cdot x^{2} -4 =\\= \frac{4}{5} \cdot (3x-5) + 2x(3x-5) \\ 4x^{2}-4=\\= \frac{12}{2}x -4 +6x^{2} - 10x \\ 4x^{2} = 2.4x +6x^{2} - 10x \\ 4x^{2}=6x^{2} - 7.6x \\ 2x^{2} -7.6x=0 $$ первый корень х=0
    второй корень х=3,8

  • Решение дробных рациональных уравнений \(\frac{5x^2+4}{5x+2} -\frac{4}{2} = 2x\)


    Решение: $$ \frac{5 x^{2} +4 }{5x+2} - \frac{4}{2} = 2x $$
    умножаем числители на общий знаменатель 2(5x+2) и сокращаем, получаем:
    $$ 10 x^{2} +8-20x-8=20 x^{2} +8x \\ -10 x^{2} -28x=0 $$
    x(-10x-28)=0
    Произведение =0, тогда, и только тогда, когда один из множитель равен 0, а другой при этом не теряет смысла
    x1=0  -10x-28=0
       x2= - 2,8

  • Решение дробных рациональных уравнений \(\frac{2x^2+4}{2x-5}-2x =\frac{4}{5}\)


    Решение: $$ \frac{2x^2+4}{2x-5} -2x= \frac{4}{5} \\ \\ \frac{2x^2+4-2x(2x-5)}{2x-5} = \frac{4}{5} \\ \\ \frac{2x^2+4-4x^2+10x}{2x-5} = \frac{4}{5} \\ \\ \frac{-2x^2+10x+4}{2x-5} = \frac{4}{5} \\ \\ 5\cdot(-2x^2+10x+4)=4\cdot(2x-5) \\ -10x^2+50x+20=8x-20 \\ -10x^2+42x+40=0 |:(-2)\\ 5x^2-21x-20=0 \\ D=441-4\cdot5\cdot(-20)=441+400=841 \\ x_1= \frac{21+29}{10}= \frac{50}{10}=5 ~~~~~~~ x_2= \frac{21-29}{10}= \frac{-8}{10}=-0,8 $$
    Ответ: $$ -0,8; 5 $$

  • Тема: Решение дробных рациональных уравнений) : (5x-8) / (х-1) =(14х+12) / (3x+5)


    Решение: Это пропорция. Произведение крайних равно произведению средних. Решение:
    (5x-8)*(3x+5)=(x-1)*(14x+12)
    15x^2 + 25x-24x-40=14x^2 + 12x - 14x - 12
    15x^2+25x-24x-40-14x^2-12x+14x+12=0
    x^2 + 3x + 28 =0
    Найдем корни по дискриминанту
    a=1; в=3; с=28
    Д= в^2 - 4ac = 9-4*1*28= -63
    ответ: нет корней.