сколько действительных корней имеет уравнение
Сколько действительных корней имеет уравнение 1+x+x^2= abs(x)
Решение: Значит, у нас тут 2 случая:1) Когда модуль положителен
1+x+x^2=x
x^2=-1 корней нет
2) Когда модуль отрицателен и мы заменяем его на противоположное значение
-1-x-x^2=x
x^2+2x+1=0
(x+1)²=0
x=-1
Сколько действительных корней имеет уравнение 9х2 - 12х + 4 = 0
Решение: D=b²-4ac
D=12²-4*9*4
D=144-144=0
Если дискриминант равен нулю,то уравнение имеет ОДИН корень.
Или,можно сказать,что уравнение имеет два ОДИНАКОВЫХ корня(что в принципе будет более верным).
$$ 9 x^{2} -12x+4=0 \\ D=144-4*4*9=144-144=0 \\ x_{0} = \frac{12}{18} = \frac{2}{3} $$
Ответ: уравнение имеет ОДИН действительный корень $$ x_{0} = \frac{2}{3} $$сколько действительных корней имеет уравнение logx(3x^2-2)=4
Решение: $$ log_{x}(3x^2-2)=4 $$Для начала найдем ОДЗ:
$$ \left \{ {{3x^2-2>0} \atop {x>0}} \right. $$
Первое уравнение решим отдельно.
3x^2 -2>0
3x^2 -2=0
x^2=2/3
$$ x_1=\sqrt{\frac{2}{3}} $$
$$ x_2=-\sqrt{\frac{2}{3}} $$
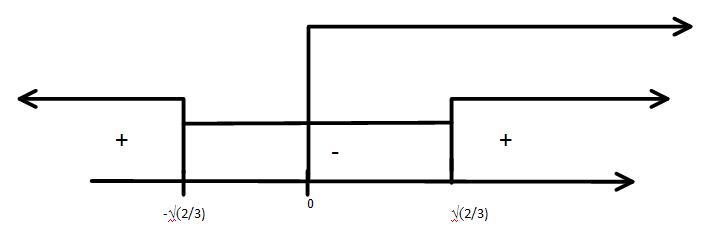
Чертим координатную прямую, отмечаем точки, расставляем знаки. Рисунок добавлю во влажения.
Решением этого уравнения будет промежуток $$ (-\infty;-\sqrt{\frac{2}{3}})\cup(\sqrt{\frac{2}{3}};+\infty) $$
А решением системы будет являться $$ (\sqrt{\frac{2}{3}};+\infty) $$
Теперь начнем решение. Представим 4 в виде логорифма по основанию x.
$$ log_x(3x^2-2)=log_x(x^4) $$
Так как основания равны, то знак логорифма можно опустить.
3x^2 -2 =x^4
x^4 - 3x^2 +2 =0
Это биквадратное уравнение. Введем обозначения
x^2 = a, $$ a\geq0 $$
a^2 -3a+2=0
По теореме Виета a1=2, a2=1
Теперь найдем х:
x^2= 2 x^2=1
$$ x_1=\sqrt{2} $$ x=±1
$$ x_2=-\sqrt{2} $$
Выберем корни, входящие в ОДЗ. Таковыми являются $$ \sqrt{2}$$ и 1.
Ответ: $$ \sqrt{2} $$ и 1
logx(3x^2-2)=4
3x^2-2=x^4
-x^4+3x^2-2=0 (-1)
x^4-3x^2+2=0
пусть x^2=t
t^2-3t+2=0
D = ( 9 / 4 ) - ( 1 * 2 ) = 1.
D>0
1) t1 = ( 3 )+v(1) / 2 = 2
2) t2 = ( 3 )-v(1) 2 = 1замена x^2=2 x^2=1
x=корен2 x=1
Сколько действительных корней имеет уравнение
x^47 + x^18 +1 = 0 ?
Решение: Для решения нужно применить теорему Штурма (формулировку теоремы можно глянуть в соответствующих источниках)f(x) = x^47 + x^18 + 1
f₁(x) = f’(x) = 47*x^46 + 18*x^17
f₂(x) = f’’(x) = 47*46x^45 + 18*17x^16
f₃(x) = f’’’(x) = 47*46*45*x^44 + 18*17*16*x^15
.....................................................
f₄₇(x) = 47*46*45*...*2
Определим знаки этих многочленов при x= -∞ и x= +∞
Для определения знака следует лите смотреть на знаки старших коэффициентов и на степени этих многочленов
Составим таблицу
f(x) f₁(x) f₂(x).... f₄₇(x) Число перемен знаков
-∞ - + - .... + 46
+∞ + + + .... + 0
Т.е. система Штурма при переходе от -∞ до +∞ теряет (46-0) перемен знаков, а поэтому многочлен имеет 46 действительных корней.
Сколько действительных корней имеет уравнение : (x^3/3)+x^2-3x+2=0
Решение: Лучше рассмотреть функционально:
1/3*x^3=-x^2+3x-2
x^3=-3x^2+9x-6=0
x^3 - кубическая парабола (стандарт)
-3x^2+9x-6 - квадратная парабола с x(в)=9/(2*3)=1.5; y(в)=-3(9/4)+9*3/2-6=
=0.75; ветви вниз; пересечение с Оx; -3x^2+9x-6=0 x1=1 x2=2
либо рисуем, либо в голове представляем=> пересечение в одной точке (где-то межде -5..-5.5) => 1 кореньСколько действительных корней имеет система x+ y=2 и xy-z^2=1
Решение: {x+y =2 ; xy -z² =1 ;
{x+y =2 ; xy =z² +1 ;
* * * x и y корни уравнения t² -2t +(z² +1) =0 (обратная теорема Виета) * * *
t² -2t +(z² +1) =0 ; * * * (t -1)² +z² =0 ⇔ z=0 ; t=1 * * *
D =1² -(z² +1) = - z² ≤0 . Имеет действительное решение, если z =
тогда t² -2t +1 =0 ⇔(t -1)² =0⇒t=1.
одно решение: x=y =1.Найдите произведение корней: (3х+1)(2х(квадрат)+х-3)=0 Сколько действительных корней имеет уравнение (3х-1)(2х(квадрат)+3х+2)=0
Сколько действительных корней имеет уравнение (2-3х(квадрат))(х(квадрат)-5х+3)=0
Решение: Решение на фото, которое прикреплено (3х+1)(2х^2+х-3)=0
3x+1=0
x=-1/3 2x^2+x-3=0 x1=1 x2=3/2
x*x1*x2= -1/3*1*3/2=-1/2
(2-3х^2)(х^2-5х+3)=0
2-3х^2=0 х^2-5х+3=0 D=25-12=13 D>0 2 корня
-3x^2=-2
x^2=2/3
x=+-2/3
ответ: 4 действительных корня
Сколько существует значений а, при которых уравнение "модуль(x^2-5*a*x)=15*a" имеет три различных действительных корня?
Решение: Итак, уравнение такое
|x^2 - 5ax| = 15a
Из уравнения сразу ясно, что a >= 0, потому что модуль >= 0.
1) При а = 0
|x^2 - 0| = 0; x = 0 - единственный корень, не подходит.
2) x^2 - 5ax = -15a < 0
x^2 - 5ax = x(x - 5a) < 0
a > 0, то есть 5a > 0, тогда 0 < x < 5a
|x^2 - 5ax| = 5ax - x^2
Подставляем
5ax - x^2 = -15a
5ax - x^2 + 15a = 0
x^2 - 5ax - 15a = 0
D = 25a^2 + 4*15a = 25a^2 + 60a > 0 при любом a > 0
x1 = (5a - √(25a^2 + 60a)) / 2; x2 = (5a + √(25a^2 + 60a)) / 2
3) 5ax - x^2 = 15a > 0
5ax - x^2 - 15a = 0
x^2 - 5ax + 15a = 0
D = 25a^2 - 4*15a = 25a^2 - 60a = 5a(5a - 12) > 0
5a(5a - 12) > 0, при этом мы знаем, что a > 0, тогда
5a - 12 > 0; a > 12/5
x1 = (5a - √(25a^2 - 60a)) / 2; x2 = (5a + √(25a^2 - 60a)) / 2
3) При а = 12/5 будет
|x^2 - 12x| = 15*12/5 = 3*12 = 36
a) x^2 - 12x = 36
x^2 - 12x - 36 = 0;
D/4 = 6^2 + 36 = 72 = (6√2)^2
x1 = 6 - 6√2; x2 = 6 + 6√2
b) x^2 - 12x = -36
x^2 - 12x + 36 = 0
(x - 6)^2 = 0
x3 = 6
При а = 12/5 будет 3 корня
Ответ: три корня будет только при а = 12/5
-х^2+11х-30<0. Можно ли найти через дискриминант, если А-отрицательный?
Решение: -х²+11х-30<0
а= -1 в= 11 с= -30
Д= в²-4ас=(-11)²-4·(-1)·(-30)=121-120=1>0⇒2 корня
-в +/-√Д -11+/-√1 -11+/-1
х=---------------= -------------- = -----------
2а 2·(-1) -2
-11+1 10
х₁= ------------- = -------------= -5
-2 -2
-11-1 -12
х₂= -----------= ----------- = 6
-2 -2
ответ: -5 и 6Про квадратичную функцию f известно, что существует ровно три значения аргумента, при которых модуль значения
функции равен 2. Сколько корней имеет уравнение f(x) = 1,1?
Решение: Ответ: ровно ДВА корня.
т. к. прямая у = 1.1 пересечется с графиком (параболой) в двух точках.
это будет или ниже или выше вершины)))
в зависимости от направления ветвей.
