решение уравнений »

число корней уравнения - страница 3

  • При каких значениях a число корней уравнения llx^2-2xl-7l=a в четыре раза больше a


    Решение:

    1) Пусть x^2 - 2x >= 0, то есть x <= 0 U x >= 2
    |x^2 - 2x - 7| = a
    |x^2 - 2x - 7| >= 0. Если a < 0, то решений нет.
    Если а = 0: x^2 - 2x - 7 = 0
    D = 2^2 + 4*7 = 32 = (4√2)^2
    x1 = (2 - 4√2)/2 = 1 - 2√2 < 0 - подходит
    x2 = (2 + 4√2)/2 = 1 + 2√2 > 2 -подходит
    Это уравнение имеет 2 корня, это НЕ в 4 раза больше 0.
    а = 0 - не подходит.
    Если a > 0, то
    а)x^2 - 2x - 7= a
    x^2 - 2x - 7 - a = 0
    D = 2^2 + 4(7 + a) = 32 + 4a = 4(8 + a)
    x1 = (2 - 2√(8+a))/2 = 1 - √(8+a)
    x2 = (2 + 2√(8+a))/2 = 1 + √(8+a)
    2 корня.
    б) x^2 - 2x - 7= -a
    x^2 - 2x - 7 + a = 0
    D = 2^2 + 4(7 - a) = 32 - 4a = 4(8 - a)
    x1 = (2 - 2√(8-a))/2 = 1 - √(8-a)
    x2 = (2 + 2√(8-a))/2 = 1 + √(8-a)
    2 корня.
    Всего 4 корня при a > 0. Значит, при а = 1
    корней будет в 4 раза больше, чем а.

    2) Пусть x^2 - 2x < 0, то есть 0 < x < 2
    |-x^2 + 2x - 7| = a
    |-x^2 + 2x - 7| >= 0. Если a < 0, то решений нет.
    Если а = 0: -x^2 + 2x - 7 = 0
    x^2 - 2x + 7 = 0 - решений нет.
    Если a > 0, то
    а) -x^2 + 2x - 7 = a 
    -x^2 + 2x - 7 - a = 0
    x^2 - 2x + 7 + a = 0
    D = 2^2 - 4(7 + a) = 4 - 28 - 4a < 0 при любом a > 0
    Решений нет.

    б)  -x^2 + 2x - 7 = -a 
    -x^2 + 2x - 7 + a = 0
    x^2 - 2x + 7 - a = 0
    D = 2^2 - 4(7-a) = 4 - 28 + 4a = 4(a-6) >= 0 при a >= 6
    x1 = (2 - 2√(a-6))/2 = 1 - √(a-6)
    x2 = (2 + 2√(a-6))/2 = 1 + √(a-6) 
    При 6 < a < 7 будет 0 < x1, x2 < 2
    2 корня, но это НЕ в 4 раза больше а
    Ответ: а = 1

  • Найдите на отрезке x∈[-π;0] число корней уравнения cos2x+cos4x+cos6x=-1/2


    Решение: См. графическое решение в приложении.
    О т в е т. 6 корней.

    Стандартные методы решения не приводят к ответу.
    Применяем формулу
    соsα+cosβ=2cos((α+β)/2) · cos ((α-β)/2)

    2cos4x·cos(-2x)+cos4x=-1/2
    2(2cos²2x-1)·cos2x+(2cos²2x-1)+1/2=0
    8cos³2x+4cos²2x-4cos2x+1=0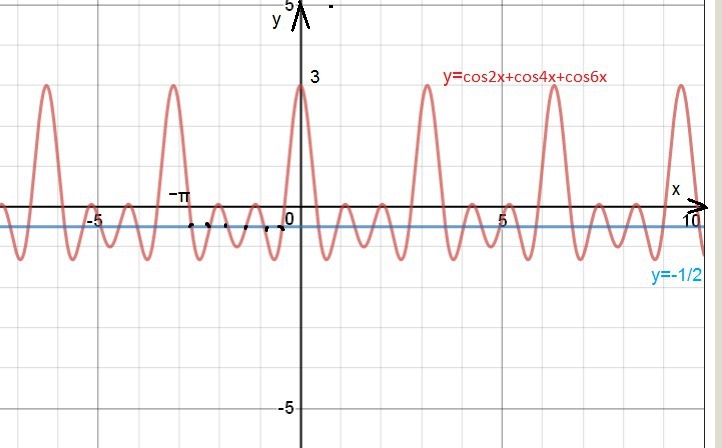 См. графическое решение в приложении.О т в е т. корней.Стандартные методы решения не приводят к ответу.Применяем формулу соs cos cos cos - cos x cos - x cos x - cos x- cos x c...

  • Найти число корней уравнения 5[Х] + 7{Х} = 2012, где [Х] - целая часть числа х, а {Х} - дробная часть числах.


    Решение: 5[x]+27{x}=2012

    Т. к. 5[x] – целое число и отнимая его от 2012 должны получить тоже целое число 27{x}.

    Отнимая от 2012 целое число 27{x} мы должны получить число, которое делится на 5, т. е. кратное 5 ( 5[x] = 2012 -  27{x} ).

    При положительных целых значениях 27{x} такое невозможно. Следовательно, решение должно быть дробным.

                Подбираем:

                1) 2012 – 27х 2/27 =2010;

                2) 2012 – 27х 7/27 = 2005;

                3) 2012 – 27х 12/27 =  2000;

                4) 2012 – 27х 17/27 =  1995;

                5) 2012 – 27х 22/27 =  1990.

                Других решений не может быть, следовательно, число корней уравнения равно 5.

  • 1. Решите уравнение 5^(2x-1)+5^(x+1)=250. Если получится 2 корня, то в ответе запишите ихпроизведение.
    2. Укажите число корней уравнения (2^x^2-32)* корень из (3-х)=0.


    Решение: 5^(2x-1) +5^(x+1)=250
    5^(-1) * 5^(2x) +5^1 * 5^x =250
    1/5 * 5^2x + 5^1 *5^x = 250
    замена переменной 5^x = t , при t>0
    1/5 t^2 + 5t =250

  • 1. Решите уравнение 5^(2x-1)+5^(x+1)=250. Если получится 2 корня, то в ответе запишите ихпроизведение.
    2. Укажите число корней уравнения (2^x^2-32)* корень из (3-х)=0.


    Решение: 1
    1/5*5^2x+5*2^x-250=0
    5^x=a
    a²+25a-1250=0
    a1+a2=-25 U a1*a2=-1250
    a1=-50⇒5^x=-50 нет решения
    a2=25⇒5^x=25⇒x=2
    2
    ОДЗ
    3-x≥0⇒x≤3
    x∈(-∞;3]
    2^x²-32=0
    2^x²=32
    x²=5
    x=-√5
    x=√5
    3-x=0
    x=3
    Ответ x={-√5;√5;3}

    1)
    5^(2x-1) +5^(x+1) =250
    5^2x * 5^(-1) +5^x *5^1 =250
    1/5 * 5^2x

<< < 123 4 5 > >>