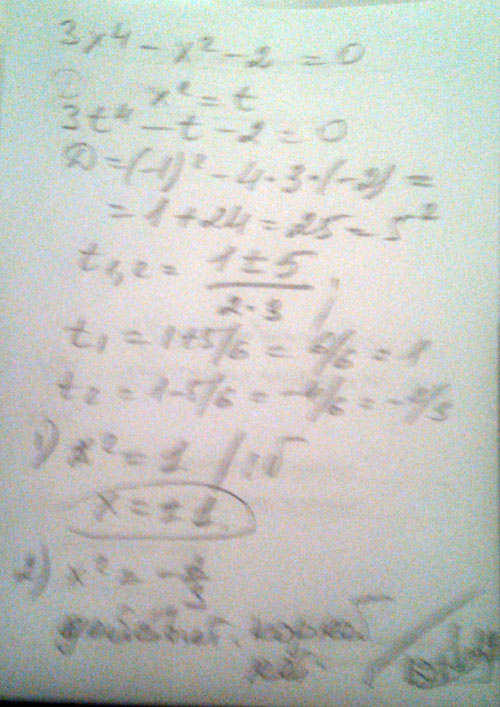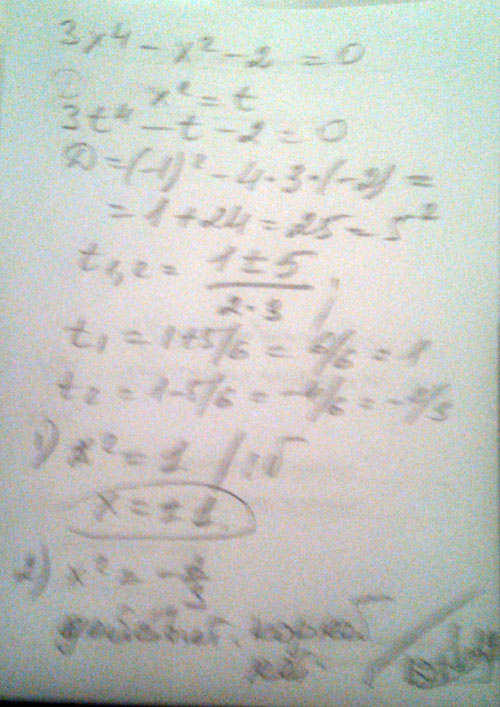корни »
действительные корни - страница 2
(10х-4)(3х+2)= 0; корень 8 * корень 5 * корень 10; х^3=81, указать число действительных корней
Решение: 1)(10x-4)(3x+2)=010x-4=0
x=2/5
3x+2=0
x=-2/3
2)
√8*√5*√10=√40*10=20
3)
x^3=81
x=log(3)81 один
1)10х-4=0 3х+2=0
х=0,4 х=-2/3
2)корень8* корень5*корень10=корень 400=20.
3)
х"3=81
один действительный корень.
Найдите действительные корни многочлена x^5+3x^4-3x^3-x^2-3x+3
Решение: Действительные корни многочлена находятся среди делителей свободного члена, т. е. 3 это числ 1: -1 : 3 : -3
подставляете их в данное уравнение и если это число обращает выражение в ноль то оно и является действительным корнем
$$ x^{5} +3 x^{4}-3 x^{3}- x^{2} -3x+3=\\= x^{2} ( x^{3}-1)+3 x^{3}(x-1)-3(x-1)=\\= x^{2} ( x^{3}-1)+3(x-1)( x^{3}-1 )=( x^{2} +3x-3)( x^{3}-1 ) $$
1 решение: x1=1
2 и 3 решение : $$ x^{2} +3x-3=0 \\ D= 3^{2} -4*1*(-3)=21 \\ x_{2}= \frac{-3+ \sqrt{21} }{2} \\ x_{3}= \frac{-3- \sqrt{21} }{2} $$Найдите действительные корни многочлена 3x^4-x^2-2
Решение: . ответ:
действительные корни
х = 1 и х = - 1
во втором случае действительных корней нет
-