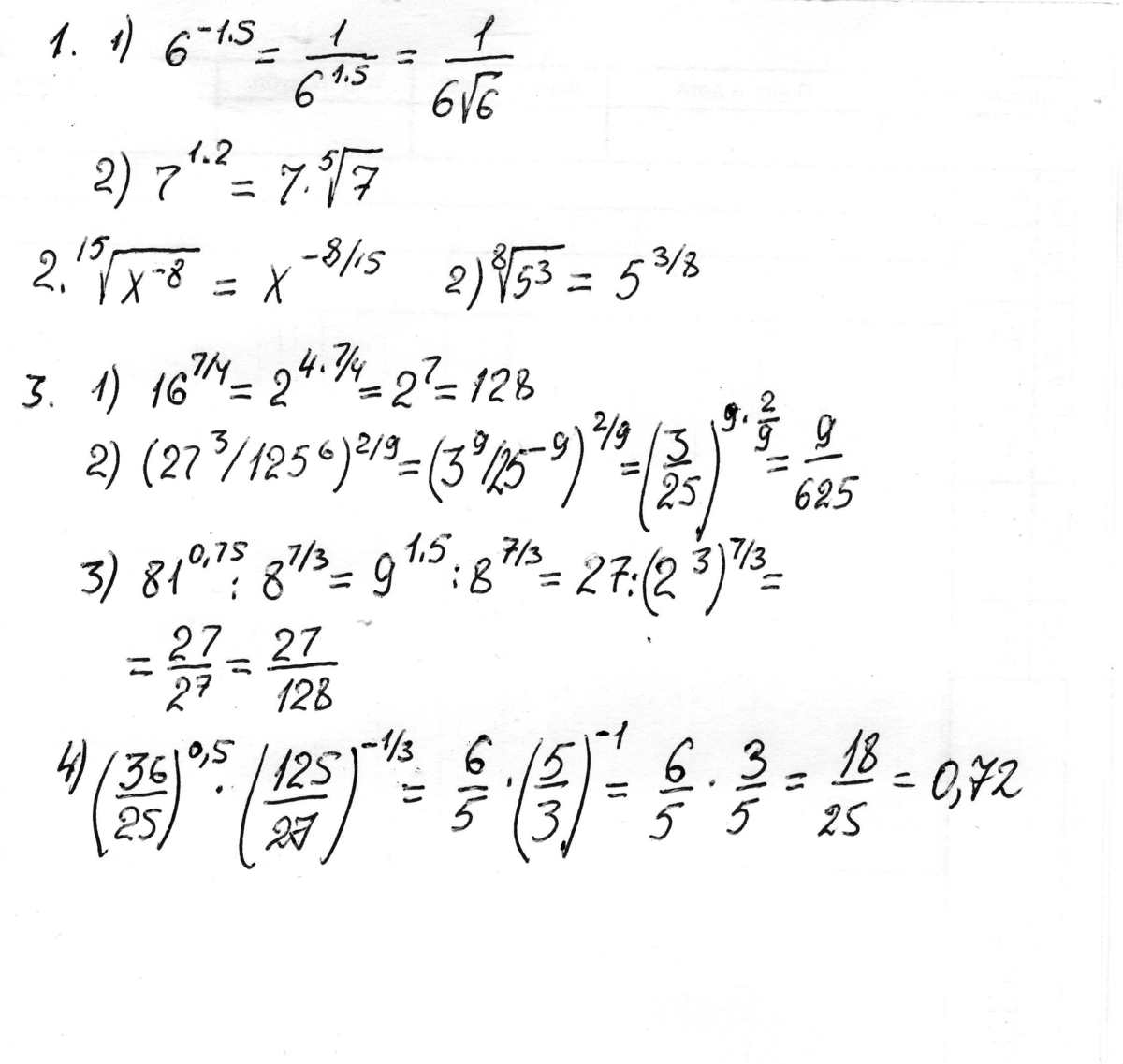корни »
найдите значение выражения под корнем - страница 2
Найдите значение выражения:√(x-10)^2(это выражение под корнем)+√(x-8)^2(это тоже под корнем) приx=√73
Решение: $$ \sqrt{(x-10)^2}+ \sqrt{(x-8)^2} =|x-10|+|x-8| $$
$$ x= \sqrt{73} \\64<73<100\\8< \sqrt{73} <10 $$
значит выражеие в первом модуле отрицательно, значит при раскрытии модуля меняем знак
а выражение во втором модуле положительно, значит модуль можно просто опустить
$$ | \sqrt{73} -10|+| \sqrt{73} -8|=- \sqrt{73} +10+ \sqrt{73} -8=2 $$№1 Напишите выражения в виде корня
1)\( 6^{-1,5;} \)
2).\( 7^{1,2;} \)
№2 Напишите корни в виде степени с рациональным показателем
1) \(\sqrt[15]{ x^{-8} } \)
2) \( \sqrt[8]{ 5^{3} } \)
№3 Найдите значения выражения
1)$$ 16^{7/4} $$
2)$$ ( 27^{3}/ 125^{6})^{2/9} $$
3) $$ 81^{0,75} :8^{7/3} $$
4) $$ (36/25)^{0,5}* (125/27)^{-1/3} $$
Решение: №1
1)$$ 1/6^3/2=1/ \sqrt{6^3} $$
2) $$ 7^6/5= \sqrt[5]{7^6} $$
№2
1)x^-8/15
2)5^3/8
№3
1)(2^4)^7/4=2^7=128
2)(3^9/5^18)^2/9=3^2*5^4=9*625=5625
3)(3^4)^0,75:(2^3)^7/3=3^3:2^7=27:128=27/128
4)((6/5)^2)^0,5*((5/3)^3)^-1/3=6/5*(5/3)^-1=6/5*3/5=18/25
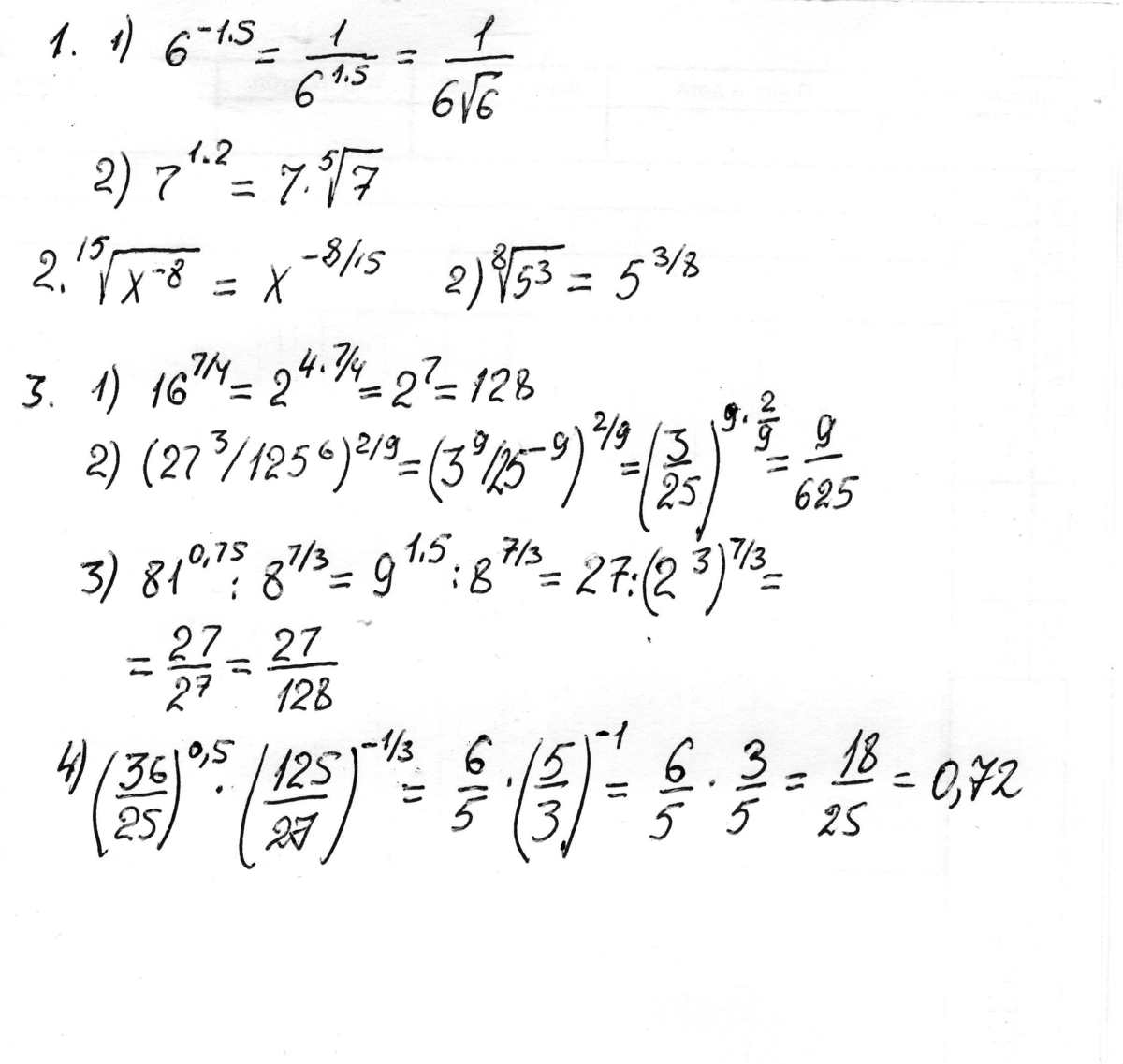
Найдите значения выражения а) корень 4 степени под корнем 3*корень 3 степени под 9 все это разделить на корень 6 степени под корнем 9* на корень под корнем3
Решение: Два способа: можно работать с корнями, а можно со степенями$$ \frac{\sqrt[4]{3\sqrt[3]{9}}}{\sqrt[6]{9\sqrt{3}}} = \frac{\sqrt[4]{\sqrt[3]{3^{3} \cdot 3^{2}}}}{\sqrt[6]{\sqrt{3 \cdot 3^{4}}}} = \frac{\sqrt[7]{3^{5}}}{\sqrt[7]{3^{5}}} = 1 $$
$$ \frac{\sqrt[4]{3\sqrt[3]{9}}}{\sqrt[6]{9\sqrt{3}}} = \frac{(3\cdot 3^{\frac{2}{3}})^{\frac{1}{4}}}{(3^{2} \cdot 3^{\frac{1}{2}})^\frac{1}{6}} = \frac{3^{\frac{5}{3}\cdot \frac{1}{4}}}{3^{\frac{5}{2}\cdot \frac{1}{6}}} = \frac{3^{\frac{5}{12}}}{3^{\frac{5}{12}}} = 1 $$