неравенства »

решите неравенство графически

  • Решить неравенство, (не графически): $$ (2 + \sqrt{3})^{\log_{2}x} + (2 - \sqrt{3})^{\log_{2}14x} \le \frac{4}{2 + \sqrt{3}} $$


    Решение: (2+sqrt(3))=a
    (2-sqrt(3))=b
    ab=1
    a^lg2(x)+b^(lg2(x)+2)<=4b
    1+b^2(lg2(x))*b^2<=4b*b^lg2(x)
    Обозначим b*b^lg2(x)= u
    1+u*u<=4u
    u*u-4u+1<=0
    (u-2)^2<=3
    2-sqrt(3)<=u<=2+sqrt(3)
    u=(2-sqrt(3))*(2-sqrt(3))^lg2(x)
    u=>2-sqrt(3) означает, что (2-sqrt(3))^lg2(x) >1 Что означает х<=1
    u<=2+sqrt(3) означает, что (2-sqrt(3))*(2-sqrt(3))^lg2(x)<=2+sqrt(3) или
     (2-sqrt(3))*((2-sqrt(3))^(lg2(x)+1))<=1
    Что значит :(lg2(x)+1)=>-1
     lg2(x)=>-2
    x=>1/4
    итак:  1/4<=x<=1

  • Решить неравенство графически : 2x - 3y > 6


    Решение: Переносим переменные по разным сторонам неравенства.
    3У<2x-6
    Y< 2/3X - 2
    2/3X>2
    X<3
    Рисуем график.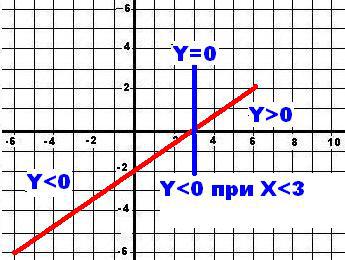
    Переносим переменные по разным сторонам неравенства. У X...

  • 8 Класс. Решить неравенство графическим способом:Х^2-3х-4 меньше либо равно 0


    Решение: Надо построить график функции у=х квадрате -3х-4, а=1, в=-3, с=-4
    характерные точки х=0 у=-4, вершина параболы (минимальное значение при х=-в/2а= 1,5 при этом нам не нужно считать у, но можно: уmin=1,5*1,5-3*1,5-4=2,25-4,5-4=-6,25
    корни x^2-3x-4 =0 находим быстро по т. Виета, х1=-1, х2=4
    Эти точки наносим на ось Х и видим, что у<0 между ними, нам подходят и сами точки.
    Ответ х∈[-1;4]

  • X^2 < 16 Решить неравенство графически


    Решение: Строим параболу y=x^2
    проводим прямую y=16 (выделена красным цветом)
    те значения икс, которые соответствуют тому, что парабола ниже прямой и будет ответ

    х∈(-4,4)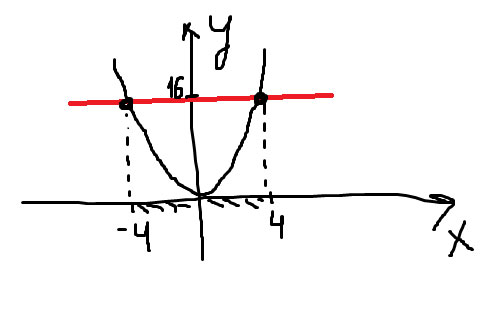

    Строим параболу y x проводим прямую y выделена красным цветом те значения икс которые соответствуют тому что парабола ниже прямой и будет ответх -...

  • Решите графически неравенство tg > -1/√3


    Решение: Рисуем единичную окружность с осями координат, через правую точку пересечения окружности с ОХ проводим вертикальную прямую, ниже оси х на этой линии отмечаем точку и соединяем ее с центром окружности и отмечаем на пересечении с окружностью незакрашенную точку, около точки пишем -1/√3 , на окружности отмечаем незакрашенными кружочками нижнюю и верхнюю точку на оси у при пересечении с окружностью -П/2 и П/2

     от точки -1/√3 отмечаем вверх по окружности штриховку до верхней точки П/2

     -1/√3 окружность единичная, значит на вертикали отмечаем точку выше -1 по у, но ниже оси х

1 2 3 > >>