неравенства »
найдите решение неравенства
Найдите решение неравенства x(x-1)(x+4)(x-5) и больше 0
Решение: Всё произведение равно нулю, если хотя бы один из множителей равен нулю, значит.
х = 0;
х - 1 = 0
х = 1;
х + 4 = 0
х = - 4;
х - 5 = 0
х = 5.
Если Вам нужны ответы больше нуля, то это х = 1 и х = 5.Распологаете числа -4 0 1 и 5 на числовой оси больше 0 начинается с 1
Найдите решение неравенства (x+2)·(3-x)>0
Решение: Решение
(x + 3)*(3 - x) > 0
Перепишем неравенство, умножая левую и правую части на (-1)
(x + 3)*(x - 3) < 0
x1 = - 3
x2 = 3 (можно через точки -3 и 3 провести параболу)
+ - +
----------------------------------------------------------------------------->
-3 3
Ответ: x∈(-3;3)Найдите решение неравенства 2-3x/4 меньше или равно 6-5x/8+1/2
Решение: $$ 2 - \frac{3x}{4} \leq 6- \frac{5x}{8} + \frac{1}{2} \\ \frac{5 x^{1}}{8} - \frac{3 x^{2} }{4} \leq 6-2+ \frac{1}{2} \\ \frac{5x}{8} - \frac{6x}{8} \leq 6-1 \\ \frac{-x}{8} \leq 5-x/8 \leq 5 \\ -x=5*8 \\ -x=40 \\ x=-40 $$Выражение: 2-3*x/4
Ответ: 2-0.75*x
Решаем по действиям:
1. 3/4=0.75
3.0|4_ _
2_8_|0.75
20
2_0_
0
Решаем по шагам:
1. 2-0.75*x
1.1. 3/4=0.75
3.0|4_ _
2_8_|0.75
20
2_0_
0
Найдите решение неравенства 2-3x/4 больше или равно 6-5x/8+1/5
принадлежащих промежутку {-5;0}
Решение: $$ 2 - \frac{3x}{4} \geq 6- \frac{5x}{8} + \frac{1}{5} \\ 80- 30x \geq 240-25x+ 8 \\ - 5x \geq 168 \\ x \leq 33.6 \\ x\in(-5;0) $$
Ответ: (-5;0)
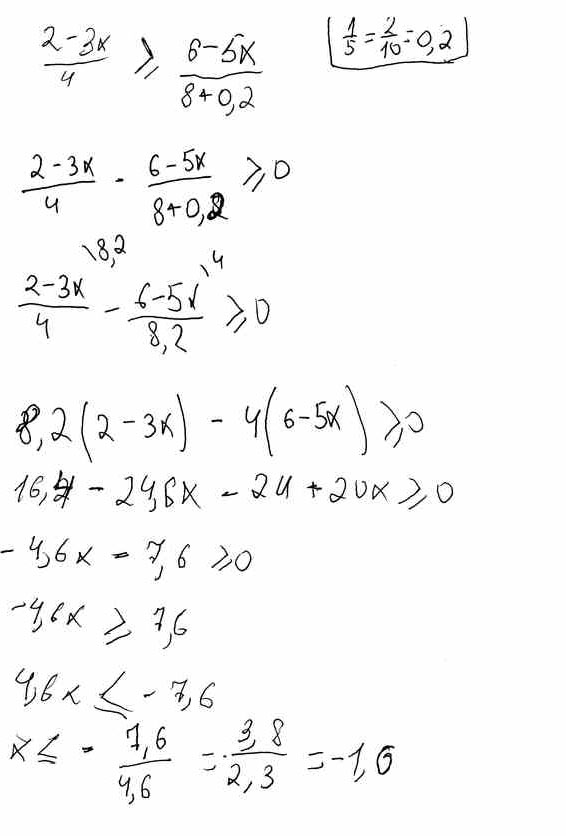
Найдите решение неравенства :2-3х/(дробь)4больше или равно 6-5х/(дробь)8 + 1/(дробь)5
Решение: Найдите решение неравенства :
если так, то...
(2-3х)/4≥ (6-5х)/8 + 1/5 ⇔
(2-3х) (6-5х) 1 10(2-3х) 5(6-5х) +8
---------≥ ----------+--- ⇔ -------------- ≥ ---------------- ⇔ 4 8 5 40 40
10(2-3х) ≥ 5(6-5х) +8 ⇔ 20-30x ≥ 30-25x+8 ⇔
5x≤-18 ⇔ x ≤-18/5

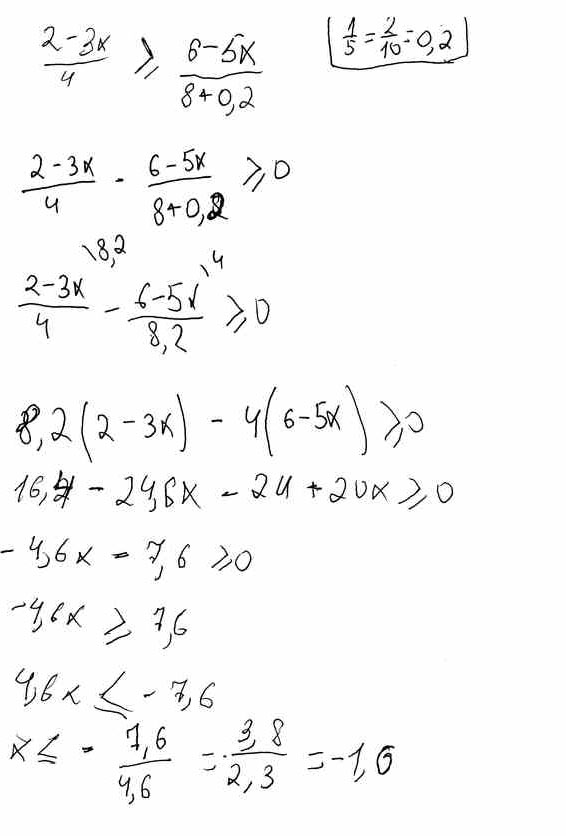
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...