неравенства »
решите неравенство используя график
Решите неравенство используя график (x в квадрате - 3 меньше 2х)
Решение: Решением будет тот промежуток по оси ОХ, на котором график y=х^2-3 ниже графика y=2x.
Решение на фото: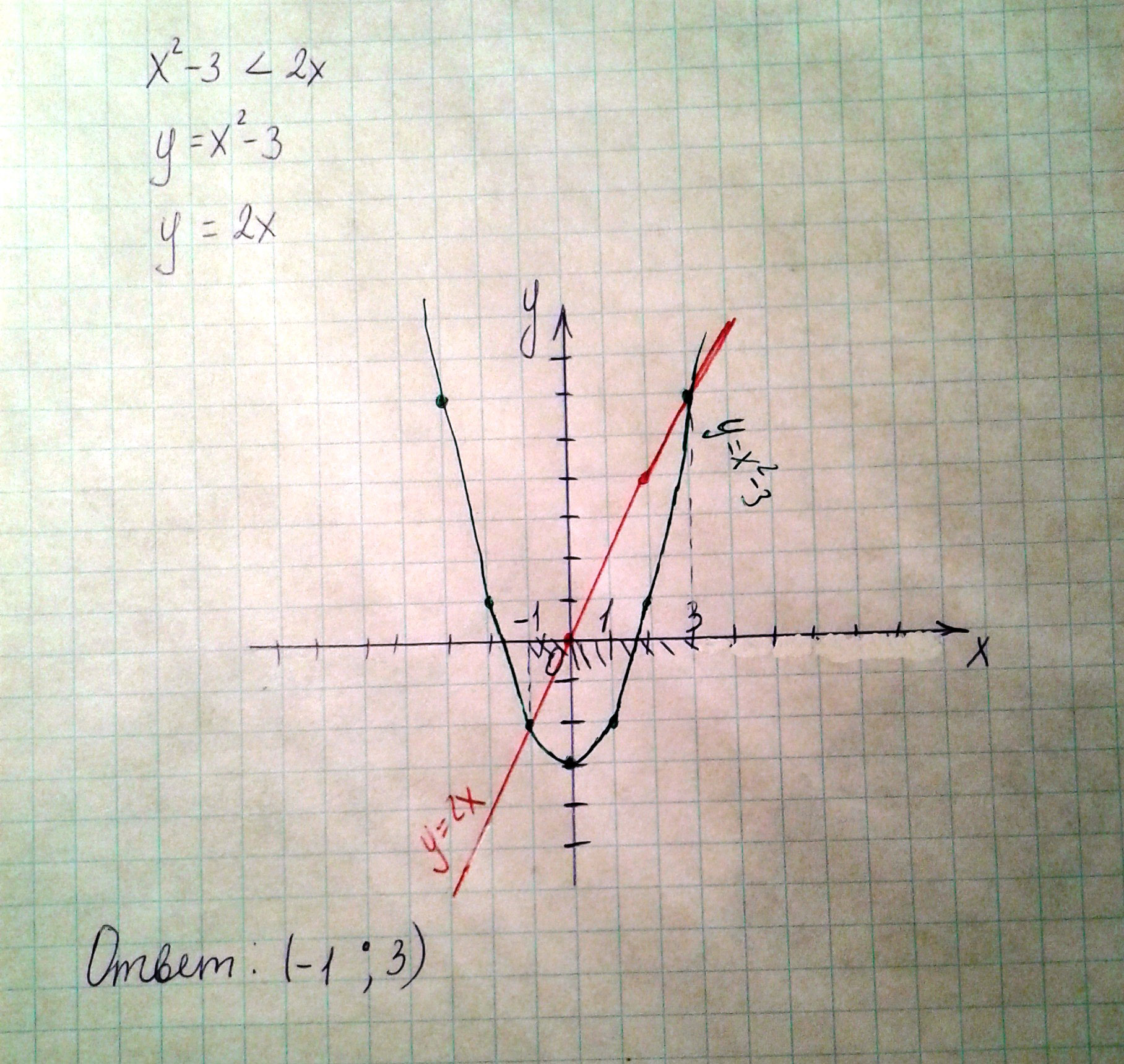
Решите неравенство, используя график х(в квадрате)-5х+4>0
Решение: Графиком квадратичной функции является парабола.
Если х>0,то ответ смотрят НАД осью,а если х<0,то ПОД осью.
В этой задаче,х>0 значит ответ находится над осью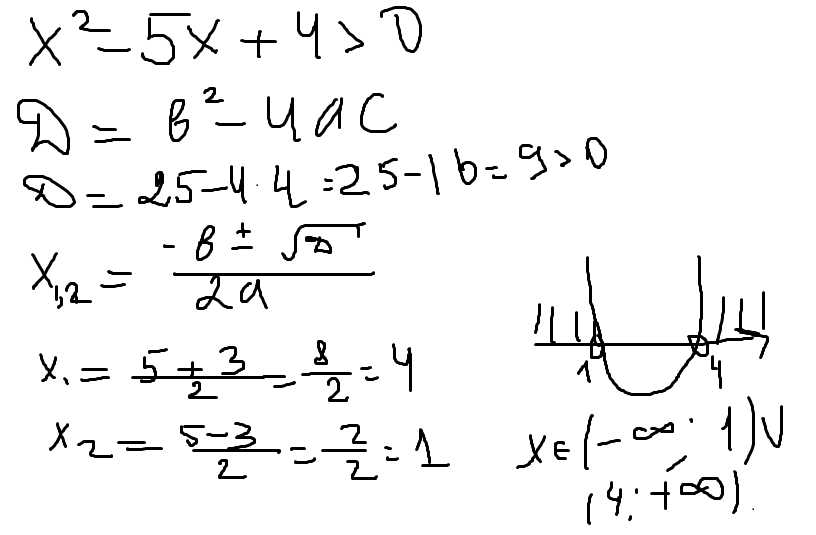
Решить у меня 2 выходит по алгебре Решите неравенство используя график 1) x^2+4x+3<02)4x^2-x-3<0
Решение: 1) x^2+4x+3 <0находим сначала корни уравнения x^2+4x+3 =0 чтобы разложить на множители
D=16-4*1*3=4
корни(х1 и х2)=-4+ или - корень из D делить все это на 2
т.е х1=(-4+2)\2=-1
х2=(-4-2)\2=-3
раскладываем на множители.
получаем( х+1)(х+3)<0
отмечаем числа на числовой прямой
это -1 и -3
ответ:(-3;-1)
2)4x^2-x-3<0
тож самое.ищем корни
D=1-4*4*(-3)=49
Х1 и х2=1+ или - корень из 49 все делим на 2
х1=(1-7)\2=-3
х2=(1+7)\2=4
раскладываем на множители:4(х+3)(х-4)<0
отмечаем на числовой прямой числа -3 и 4
Ответ:(-3;4)
Дан график функции
y=x²-4x
Используя график, решите неравенство x²>4x
Решение: x² > 4x
x² - 4x > 0
Значит нас интересуют такие значения х, при которых функция положительна.
Смотрим на график, данная функция положительна на двух интервалах:
( - ∞; 0 ) и ( 4 ; + ∞)
ОТВЕТ: ( - ∞; 0 ) V ( 4 ; + ∞) ,
На рисунке изображен график функции
y= x² - x - 6
Используя график, решите неравенство
x² - x - 6 > 0
Решение: Если решать это задание, используя график, то решением неравенства будет та часть параболы, где ветви параболы выше оси OX. Следовательно решением неравенства будет промежуток $$ (- \infty; -2) \cup (3;+ \infty) $$. Также ответ можно записать в виде неравенства 3Ответ: $$ (- \infty; -2) \cup (3;+ \infty) $$ или 3


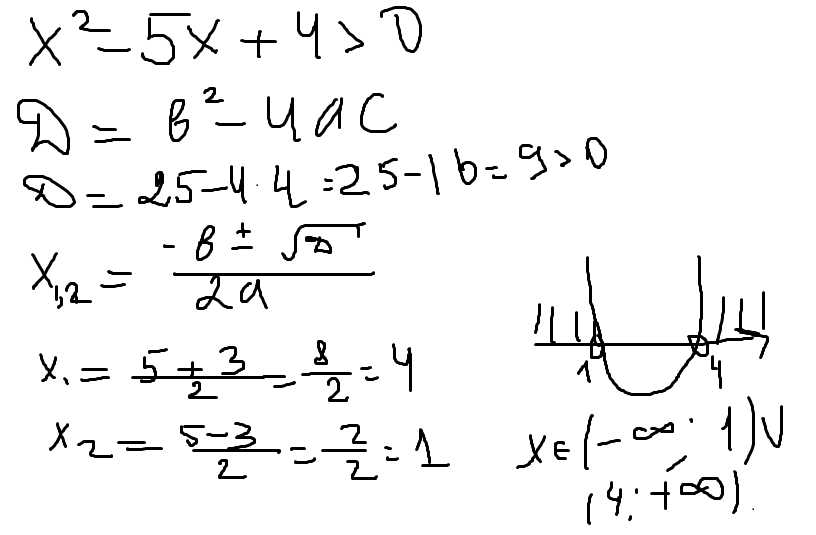
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...