решите неравенство под корнем
Решить неравенство: под корнем(4x^2-16x+12) + под корнем(8x-2x^2-6) меньше 2x-2
Решение: Вариант 1 $$ \sqrt{4x^2-16x+12} + \sqrt{8x-2x^2-6}< 2x-2; $$
$$ \sqrt{4( x-1)( x-3)} + \sqrt{-2( x-1)( x-3)}< 2x-2; $$
ОДЗ: $$ 2x-2 \geq 0; x\in [1;\infty); $$
$$ -2( x-1)( x-3)\geq0;x\in [1;3] $$
$$ 4( x-1)( x-3)\geq0;x\in (-\infty;1]\cup [3;\infty); $$
Получаем в ОДЗ входит только одно число х=1
Подставим х=1: 0+0<0, число х=1 не явл корнем
Ответ корней нет
Вариант решения 2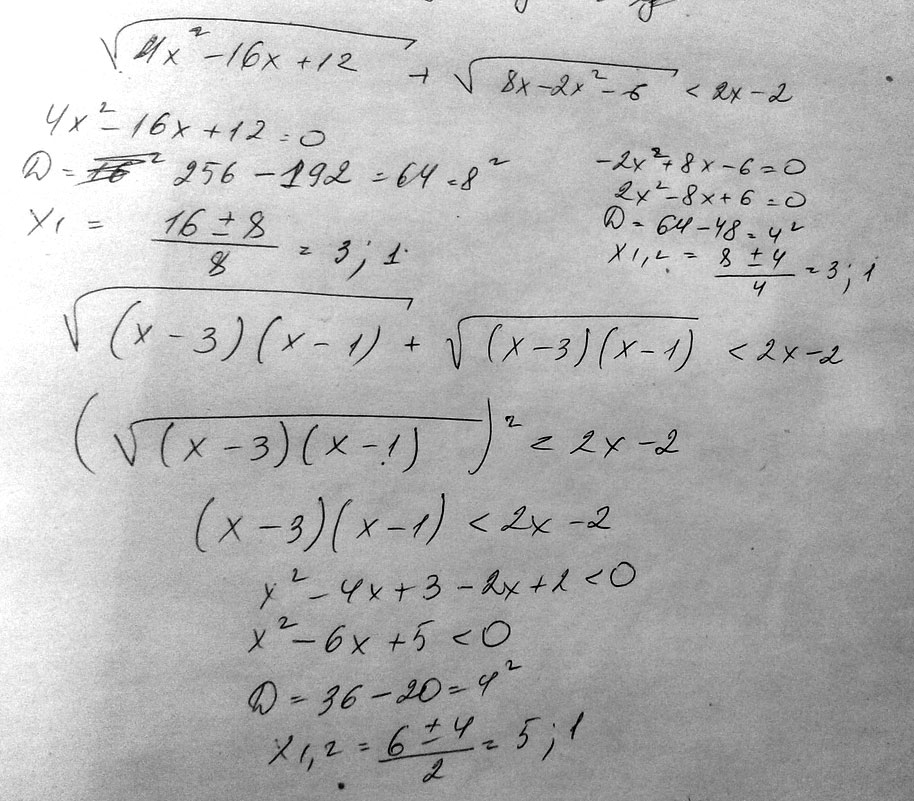
(√x+3)<(√x-1+√x-2) цифры и (+-) все под корнем, нужно решить неравенство
Решение: ОДЗ х>=2
(√(x+3)) <(√(x-1)+√(x-2))
(√(x+3)) >=0 и (√(x-1)+√(x-2)) >=0
значит можно возвести в квадрат
(√(x+3)) ^2<(√(x-1)+√(x-2))^2
(x+3)<((x-1)+(x-2)+2√((x-1)(x-2)))
(6-x)<(2√((x-1)(x-2)))
1) если 6-x < 0 то неравенство верно при всех одз
6-x < 0 и х>=2 => х>6
2) если 6-x >= 0 то неравенство можно возвести в квадрат
(6-x)^2<(2√((x-1)(x-2)))^2
36-12х+x^2<(4(x^2-3х+2))
28<3x^2
/х/ > корень(28/3)~ 3,055050463
6-x >= 0 и /х/ > корень(28/3) и х>=2 => корень(28/3)< х <=6
объединяем 2 ответа и получаем
ответ х > корень(28/3)Решите неравенство методом равносильных преобразований (x-1)·√x²+1≤x²-1 (x²+1-полностью под корнем)
Решение: $$ (x-1) \sqrt{ x^{2} +1} \leq (x-1)(x+1) \\ x^{2} +1 \geq 0=> x \in R \\ (x-1) (\sqrt{ x^{2} +1}-x-1) \leq 0 \\ x-1 \geq 0=>x \geq 1 \\ \sqrt{ x^{2} +1} ^2 \geq (x+1)^2 \\ x^{2} +1 \geq x^{2} +2x+1 \\ 2x \leq 0 \\ x \leq 0 \\ \\ =>x\in (- \infty;0] \cup [1;+\infty) $$
решите неравенство √x²-3x-10<8-x
√x²-3x-10-всё под корнем
Решение: Поскольку Х² - 3 * Х - 10 = (Х + 2) * (Х - 5), то область определенияХ ∈ ( - ∞ ; -2] ∨ [ 5 ; = )
При Х > 8 неравенство не выполняется, так как левая часть положительна, а правая отрицательна. При Х < 8 обе части можно возвести в квадрат
Х² - 3 * Х - 10 < (8 - X)² = X² - 16 * X + 64
13 * X < 74
X < 74 / 13
Итак Х ∈ ( - ∞ ; -2 ] ∨ [ 5 ; 74/13 )
$$ \\\sqrt{x^2-3x-10}<8-x\\ x^2-3x-10\geq0 \wedge 8-x\geq0\\ x^2+2x-5x-10\geq 0\wedge -x\geq -8\\ x(x+2)-5(x+2)\geq 0 \wedge x\leq 8\\ (x-5)(x+2)\geq 0 \wedge x\leq 8\\ x\in(-\infty,-2>\cup <5,\infty) \wedge x\leq 8\\ x\in(-\infty,-2>\cup <5,8>\\\\ x^2-3x-10<(8-x)^2\\ x^2-3x-10<64-16x+x^2\\ 13x<74\\ x<\frac{74}{13}\\\\ x\in(-\infty,-2>\cup <5,8> \wedge x<\frac{74}{13}\\ \underline{x\in(-\infty,-2>\cup <5,\frac{74}{13})} $$
Решить неравенство. √x^2 - 5x < √6 (x^2 - 5x полностью под корнем)
Решение: Сначала область определения, под корнем неотрицательное.x^2-5*x>=0
x*(x-5)>=0, методом интервала находим x<=0 и x>=5. Возводим обе части неравенства в квадрат. Так как считаем, что результат извлечения квадратного корня – число неотрицательное, то неравенство только усилится. Получаем:
x^2-5*x-6<0
Корни уравнения х1=-1, х2=6
Также методом интервала получаем в качестве решения промежуток (-1;6). Су учётом найденной выше области определения получаем окончательный ответ: (-1;0] и [5;6)

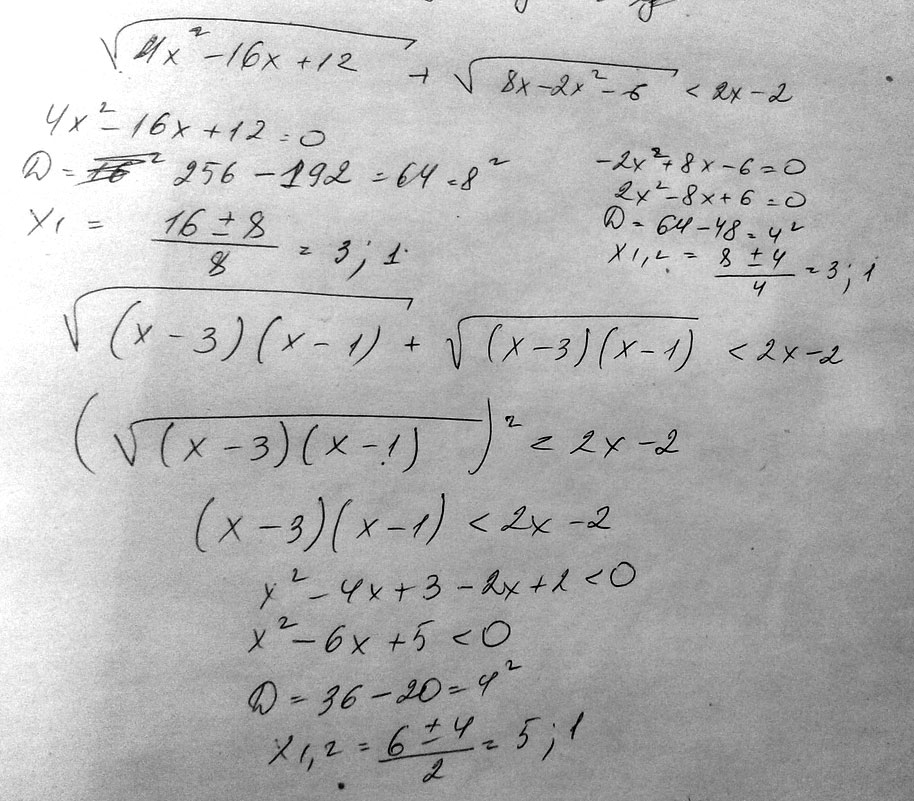

 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...