неравенства »

решить неравенство через дискриминант

  • Решить неравенство через дискриминант
    3х в квадрате - 6х + 5 > 0


    Решение: 3x^2 - 6x+5 > 0
    D = 36 - 3*4*5= - 24
    Т.к. дискриминант отрицательный, значит парабола не пересекает ось 0x.
    Строим схематичный график параболы,  ветви направлены вверх, т.к. a > 0.  Т.к. знак неравенства больше, то х может принимать любы значения.
    Ответ: от минус бесконечности до плюс бесконечности.

  • Решите неравенство через дискриминант

    x³- 81x ≥ 0


    Решение: Выражение: $$ x^2-81*x=0 $$ Ответ:$$ x^2-81*x=0 $$ Решаем уравнение $$ x^2-81*x=0 $$ Квадратное уравнение, решаем относительно x: Ищем дискриминант:$$ D=(-81)^2-4*1*0=6561-4*0=6561; $$ Дискриминант больше 0, уравнение имеет 2 корня: $$ x_1=(2\sqrt6561-(-81))/(2*1)=(81-(-81))/2=(81+81)/2=162/2=81;\\ x_2=(-2\sqrt6561-(-81))/(2*1)=(-81-(-81))/2=(-81+81)/2=0/2=0. $$

    Выражение  x - x Ответ  x - x Решаем уравнение  x - x Квадратное уравнение  решаем относительно x Ищем дискриминант D - - - Дискриминант больше уравнение имеет корня x sqr...

  • Решить квадратное неравенство по дискриминанту.1) (2х - 1)^2 < 4x + 61
    2) -3(x^2 + 1) ≥ 3x - 39


    Решение: 1. 4x²-4x+1 < 4 x + 61
      4 x² - 8 x - 60 < 0
      x² - 2 x - 15 < 0
      D = (-2)²- 4 ·1 ·(-15)= 4 + 60 = 64 = 8²
      x 1 = (2 - 8)/ 2 = -3
      x 2 = (2 + 8) / 2 =5
     Если D > 0 , a = 1 >0 - ветви параболы направлены вверх ⇒
     ⇒ решения нераввенства находятся внутри промежутка между корнями : -3 < x < 5
    2. -3 (x² + 1 ) ≥ 3 x - 39 Сократим на ( - 3 )
      x² + 1 ≤ x - 13
      x² - x + 14 ≤ 0
      D = ( -1)² - 4 ·1 ·14 = 1 - 56 = - 55 < 0 ⇒ корней нет
      a = 1 > 0 - ветви параболы направлены вверх , вся парабола находится выше оси Х , отрицательных значений не принимает .
      Ответ : ∅

  • Х в квадрате - 7х +12(знак меньше) 17-3х. Решить неравенство и дискриминант из него


    Решение: Х^2-7x+12<17-3x
    x^2-4x-5<0
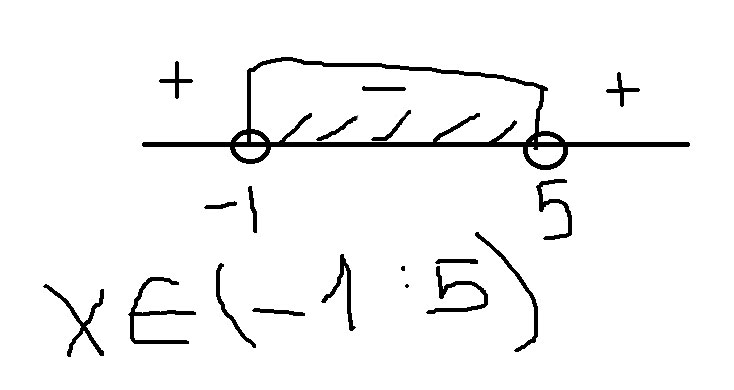
    (x+1)*(x-5)<0
    1

    X^2-7x+12<17-3x
    x^2+3x-7x+12-17<-
    x^2-4x-5<0
    d=4^2-4*1*9*(-5)=16+20=36
    x1,2=4+-6/2
    x1=5
    x2=-1
     

    Х - x...

  • Помогите.С дискриминантом.
    Решите неравенство. В ответе укажите длину промежутка,который является решением неравенства
    -2x^2+9x-4>=0


    Решение: Сначала все домножим на -1
    2х2-9х+4>либо равно 0
    Д. 9*9-4*8 рвно 49
    найдем х х1. равен 9+7 деленное на 4 равно 4
    х2 равен 9-7 деленное на 4 равно 0.5
     исходя из выше решенного х больше или равен от0.5 в квадратных скобках до плюс бесконечнгости..... так как 4 входит в этот промежуток

1 2 3 > >>