найдите целочисленное решение неравенства
Найдите наименьшее целочисленное решение неравенства 2х-5<4х+7
Решение: 2x-5<4x+72x-4x<7+5
-2x<12
x>12/-2
x>-6
$$ 2x-5<4x+7 $$
$$ 2x-4x<7+5 $$
$$ -2x<12 $$
$$ 2x>-12 $$
$$ x>-6 $$
Наименьшее целочисленное решение неравенства: x=-5
Ответ: x=-5
Найдите наименьшее целочисленное решение неравенства
7(х+2)-3(х-8)>10
Решение: 7(x+2)-3(x-8)>10,
7x-3x>25,
4x>25,
x>6,25
Ответ: 7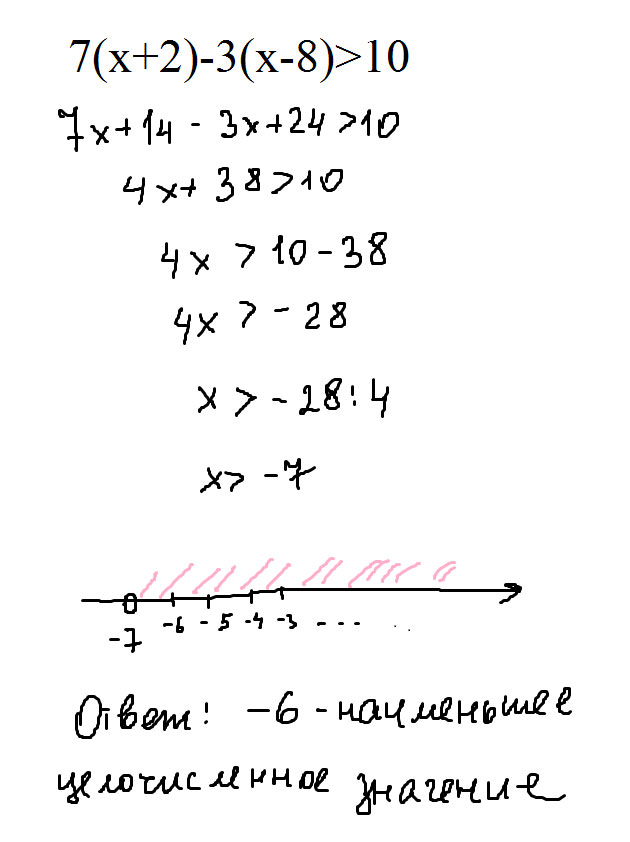
Найдите наибольшее целочисленное решение неравенства 2,5^(2x + 3) <= 6,25
Решение:$$ 2,5^{2x+3} \leq 6,25 \\ \ 2,5^{2x+3} \leq 2,5^{2} \\ \ 2x+3 \leq 2 \\ \ 2x \leq -1 \\ \ x \leq - \frac{1}{2} \\ \ x \leq - 0,5 $$
-/-/-/-/-/-/-/-/-/-/-/-/-/--|-/-//-/--|--------------------->
-1 -1/2
-1 - наибольшее целое решение неравенстваСначала решаете это неравенство, а потом из множества решений находите наибольшее целое число. Теперь решаем неравенство. 6.25=2.25^2, поэтому переписываем это неравенство в виде:
2.5^(2x+3)≤2.5^2.
Основания одинаковы, поэтому данное неравенство напишем следующим образом:
2x+3≤2, решаем данное очень простое неравенство.
2x≤-1
x≤-1/2,
наибольшим целочисленным решением является число -1.1) При каких значениях х график функции у=4х-9 расположен выше оси х 2) Найдите наименьшее целочисленное решение неравенства3х-4больше2х+3 3).решите неравенство 4-х(в квадрате)меньше0
Решение: 1) y=4x-9
4x-9>0
4x>9
x>2,25
2) 3x-4>2x+1
3x-2x>1+4
x>5
x=6 - наименьшее целочисленное решение неравенства
3) 4-x²<0
-x²+4<0
x² -4>0
(x-2)(x+2)>0
x=2 x= -2
+ - +
------- -2 ----------- 2 ------------
\\\\
x<-2
x>2
x∈(-∞; -2)U(2; +∞)
4)
5x-3x²+2≥0
3x²-5x-2≤0
3x²-5x-2=0
D=25+24=49
x₁=(5-7)/6= -2/6= -1/3
x₂=(5+7)/6=2
+ - +
---------- -1/3 -------------- 2 ----------------
\\\\\\\\
x∈[-1/3; 2]Найдите целочисленное решение неравенств (x+5)*(x+1)^2*(x-1)<0
Решение: (x+5)·(x+1)²·(x-1)<0
(х+1)²-положительное число, поэтому рассмотрим неравенство
(х+5)(х-1)<0
На числовой прямой отметим нули неравенства
++++-5------1+++++
видно, что отрицательное значение принимает при х∈(-5;1)
Целые значения, которые будут решением неравенства : х=-4;-3;-2;-1;0

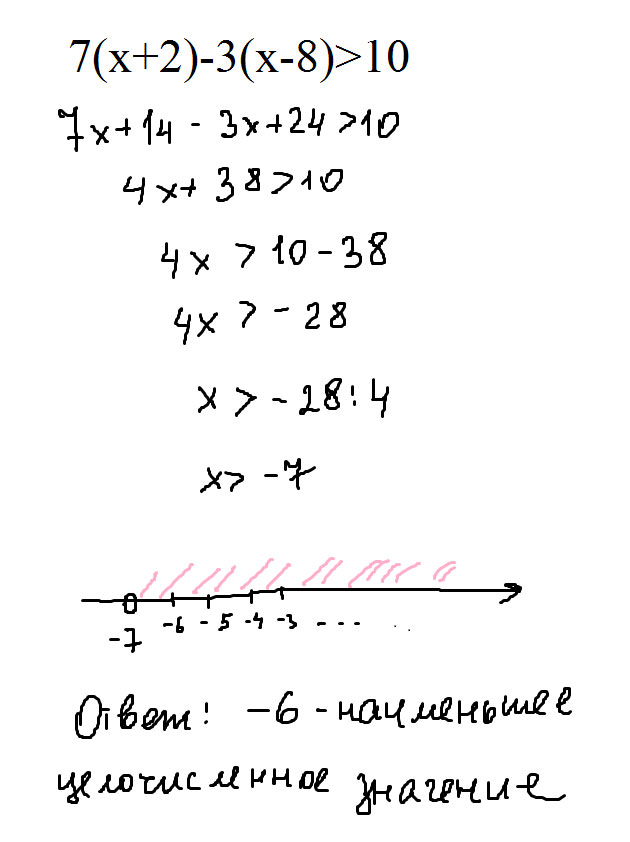
 Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то...
Если числа a и b равны между собой, то a - b = 0. Если же числа a и b не равны между собой, то разность a - b либо положительна, либо отрицательна.
Если разность a - b положительна, то говорят, что число a больше числа b; записывается это таким образом:
a > b. (1)
Если разность a - b отрицательна, то... Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...
Линейные неравенства
Так называются неравенства, левая и правая части которых представляют собой линейные функции относительно неизвестной.величины. К ним относятся, например, неравенства
2x - 1 > - x + 3; 7x 4 - 6x; 9 - x < x + 5
и т. д. Для определенности мы рассмотрим лишь неравенства, содержащие знак >. Линейное неравенство, содержащее знак >, имеет вид:
ах + b >...