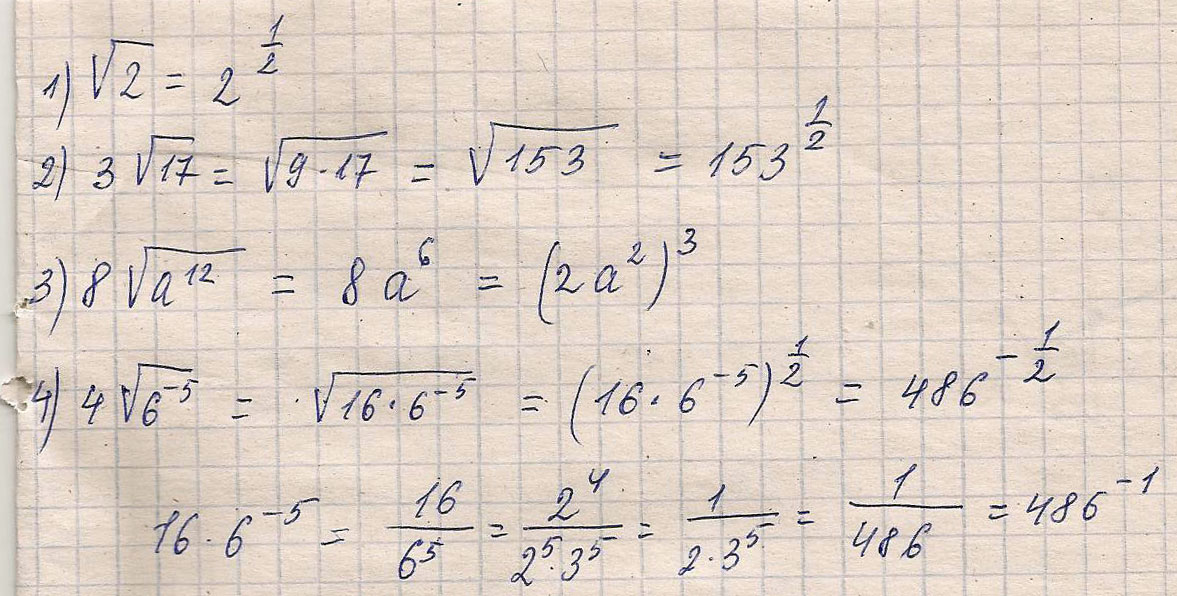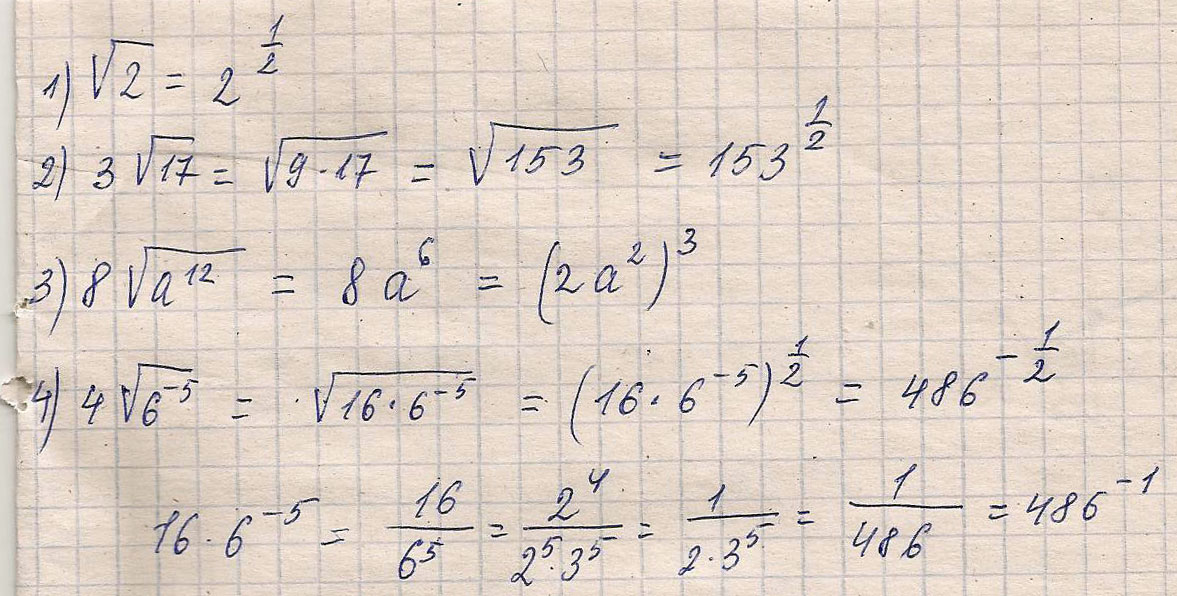степень с рациональным показателем
27в степени -2/3*9-2; тема степень с рациональным показателем.
Решение: 27 ^ ( - 2/3 ) = ( 3^3 ) ^ ( - 2/3 ) = 3 ^ ( - 2 )
9 ^ ( - 2 ) = ( 3 ^ 2) ^ ( - 2 ) = 3 ^ ( - 4 )
----------
3 ^ ( - 2 ) * 3 ^ ( - 4 ) = 3 ^ ( - 2 - 4 ) = 3 ^ ( - 6 )
-----------
Ответ 3 ^ ( - 6 ) или 1 / ( 3 ^ 6 )-2/3*9 = -18/3. Дальше -18/3 - 2 = -18/3 - 6/3 = -24/3 = -8 степень.
Теперь при возведении 27 в -8 степень у нас получается 1 / 27^8Представьте в виде степени с рациональным показателем: \(a^{\frac{2}{5}}b^{-\frac{3}{4}}c^{\frac{1}{2}}\cdot a^{-\frac{3}{5}}b^{\frac{1}{2}}c^{-\frac{1}{3}}\)
Найдите значение \((\frac{a^{-\frac{3}{5}}b^{-\frac{3}{5}}\sqrt[5]{b^{-3}}}{(ac)^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc)^{-3} \;\;\text{при}\;\; a=32; b=c=\frac{1}{3}\)
Решение: [a^(2/5)]·[b^(-3/4)]·[c^(1/2)]·[a^(-3/5)]·[b^(1/2)]·[c^(-1/3)]=
=[a^((2/5)-3/5))]·[b^((-3/4+1/2))]·[c^(1/2-1/3)]=
=[a^(-1/5)]·[b^(-1/4)]·[c^(1/6)]
{a^(-3/5)·b^(-3/5)·∛(b⁻³)/[(ac)^(-4/5)·b^(-7/5)] + 9bc}^(-3)=
=[(a^(1/5)b^(-1/5)c^(4/5)+9bc)]^(-3)=
b=c=1/3 a=32=2⁵ (a^(1/5)=(2⁵ )^(1/5) =2 тогда
=[2c^(3/5)+9c²]^(-3)=[2(1/3)^(3/5)+1]^(-3)
$$ 1)\; \; a^{\frac{2}{5}}b^{-\frac{3}{4}}c^{\frac{1}{2}}\cdot a^{-\frac{3}{5}}b^{\frac{1}{2}}c^{-\frac{1}{3}}=a^{\frac{2}{5}-\frac{3}{5}}\cdot b^{-\frac{3}{4}+\frac{1}{2}} \cdot c^{\frac{1}{2}-\frac{1}{3}}=\\\\=a^{-\frac{1}{5}}\cdot b^{-\frac{1}{4}}\cdot c^{\frac{1}{6}}=\frac{c^{\frac{1}{6}}}{a^{\frac{1}{5}}}\cdot b^{\frac{1}{4}}=\frac{\sqrt[6]{c}}{\sqrt[5]{a}\sqrt[4]{b}}\\\\2)\; \; a=32,b=c=\frac{1}{3}\\\\\left ( \frac{a^{-\frac{3}{5}}b^{-\frac{3}{5}}\cdot \sqrt[5]{b^{-3}}}{(ac)^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc\right )^{-3}= \\ =\left (\frac{a^{-\frac{3}{5}}b^{-\frac{6}{5}}}{a^{-\frac{4}{5}}c^{-\frac{4}{5}}b^{-\frac{7}{5}}}+9bc\right )^{-3}=\left (a^{\frac{1}{5}}b^{\frac{1}{5}}c^{\frac{4}{5}}+9bc)\right )^{-3}=\\\\=\left (\sqrt[5]{32\cdot \frac{1}{3}\cdot \frac{1}{3^4}}+9\cdot \frac{1}{3}\cdot \frac{1}{3}\right )^{-3}=\left (\sqrt[5]{2^5\cdot \frac{1}{3^5}}+9\cdot \frac{1}{3^2}\right )^{-3}=\\\\=\left (\frac{2}{3}+1\right )^{-3}=(\frac{5}{3})^{-3}=\frac{27}{125} $$
Найдите значение выражения \(\frac{(m-n)^{\frac{4}{9}}(m-n)^{\frac{2}{9}}(m-n)^{\frac{1}{3}}}{m^{\frac{1}{2}}+n^{\frac{1}{2}}}\) при m=90,25; n=30,25
Упростите выражение: \((m+n):(m^{\frac{3}{2}}-m^{\frac{1}{3}}n^{\frac{1}{3}}+n^{\frac{2}{3}})\)
Решение: 1
$$ (m-n) ^{4/9+2/9+1/3) } /( \sqrt{m} + \sqrt{n} )=(m-n)/( \sqrt{m} - \sqrt{n} )= $$(√m-√n)(√m+√n)/(√m+√n)=√m-√n
m=361/4 n=121/4
√(361/4)-√(121/4)=19/2-11/2=8/2=4
2
(∛m+∛n)(∛m²-∛(mn)+∛n²)/(∛m²-∛(mn)+∛n²)=∛m+∛n
1) Степени с рациональным показателем. Вычислите:81(в степени 0.75)*32(в степени минус 0.4)-8(в ст. минус 2/3-дробь)*27(в ст. дробь 1/3)+256(в ст.0.5)
2)(2+15(в ст.0.25))(2-15(в ст.0.25))*(4-корень из 15(в ст. минус 1)
Решение: $$ 81^{0,75}*32^{-0,4}-8^{-\frac{2}{3}}*27^{\frac{1}{3}}+256^{0,5}= \\ (3^4)^{\frac{3}{4}}*(2^5)^{-\frac{2}{5}}-(2^3)^{-\frac{2}{3}}*(3^3)^{\frac{1}{3}}+(16^2)^{\frac{1}{2}}= \\ =3^3*2^{-2}-2^{-2}*3+16=27*\frac{1}{4}-\frac{1}{4}*3+16=\frac{1}{4}(27-3)+16 \\ \frac{1}{4}(27-3)+16=\frac{1}{4}*24+16=6+16=22 \\ (2+15^{0,25})(2-15^{0,25})*(4-\sqrt{15^{-1}})= \\ (4-(15^{0,25})^2)*(4-\sqrt{15^{-1}})=(4-15^{0,5})*(4-\sqrt{15^{-1}}) \\ (4-15^{0,5})*(4-15^{-0,5})=16-4*15^{-0,5}-4*15^{0,5}+1= \\ 17-4*\frac{1}{\sqrt{15}}-4\sqrt{15}=\frac{17\sqrt{15}-4-60}{\sqrt{15}}=\frac{17\sqrt{15}-64}{\sqrt{15}} $$Представьте выражение в виде степени с рациональным показателем корень из 2, 3корня из 17, 8 корней из а в 12ой степени, 4 корня из 6 в -5 степени?
Решение: 1) V 2 = 2 ^ 1\2 (два в степени 1\2)2) 3 V 17 = V 9 * 17 = V 153 = 153 ^ 1\2
3) 8 V A ^ 12 = 8 * A ^ 6 = 2 ^ 3 * A ^6 = (2A^2)^3
4) (4 V 6 ) ^-5 = (V 6 * 16 )^-5 = (V 2*3 * 2^4 )^-5 = (V 3* 2^5)^-5 = (1\3)^5 * (2)^-25