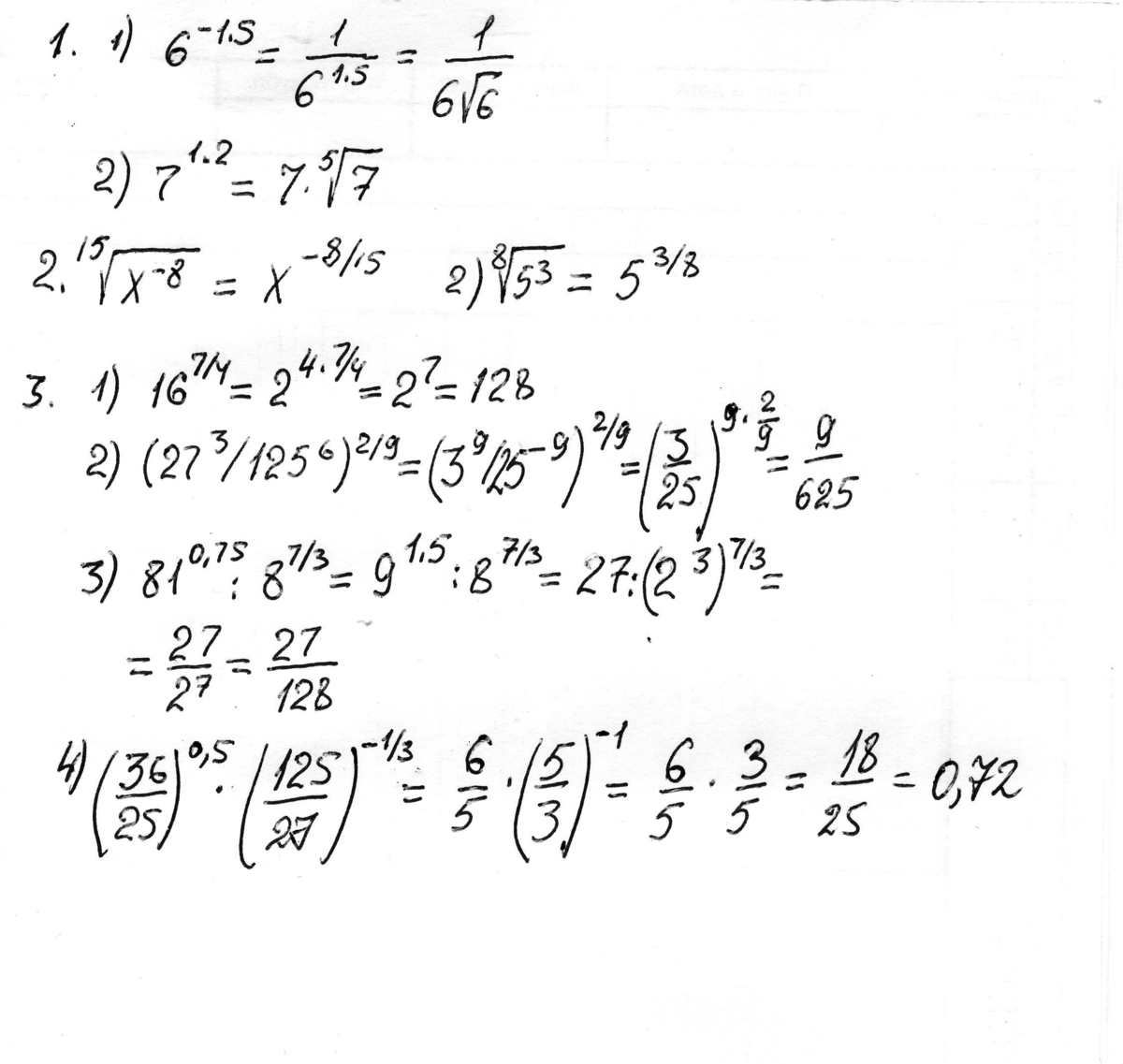степени »
степень с рациональным показателем - страница 2
Степень с рациональным показателем.
№1
напишите выражения в виде корня
1)\( 6^{-1,5;} \)
2).\( 7^{1,2;} \)
№2
напишите корни в виде степени с рациональным показателем
1)\( \sqrt[15]{ x^{-8} } \)
2)\( \sqrt[8]{ 5^{3} } \)
№3
найдите значения выражения
1)\( 16^{7/4} \)
2)\( ( 27^{3}/ 125^{6})^{2/9} \)
3)\( 81^{0,75} :8^{7/3} \)
4)\( (36/25)^{0,5}* (125/27)^{-1/3} \)
Решение: №1
1)1/6^3/2=1/\(\sqrt{6^3}\)
2)7^6/5=\(\sqrt[5]{7^6}\)
№2
1)x^-8/15
2)5^3/8
№3
1)(2^4)^7/4=2^7=128
2)(3^9/5^18)^2/9=3^2*5^4=9*625=5625
3)(3^4)^0,75:(2^3)^7/3=3^3:2^7=27:128=27/128
4)((6/5)^2)^0,5*((5/3)^3)^-1/3=6/5*(5/3)^-1=6/5*3/5=18/25
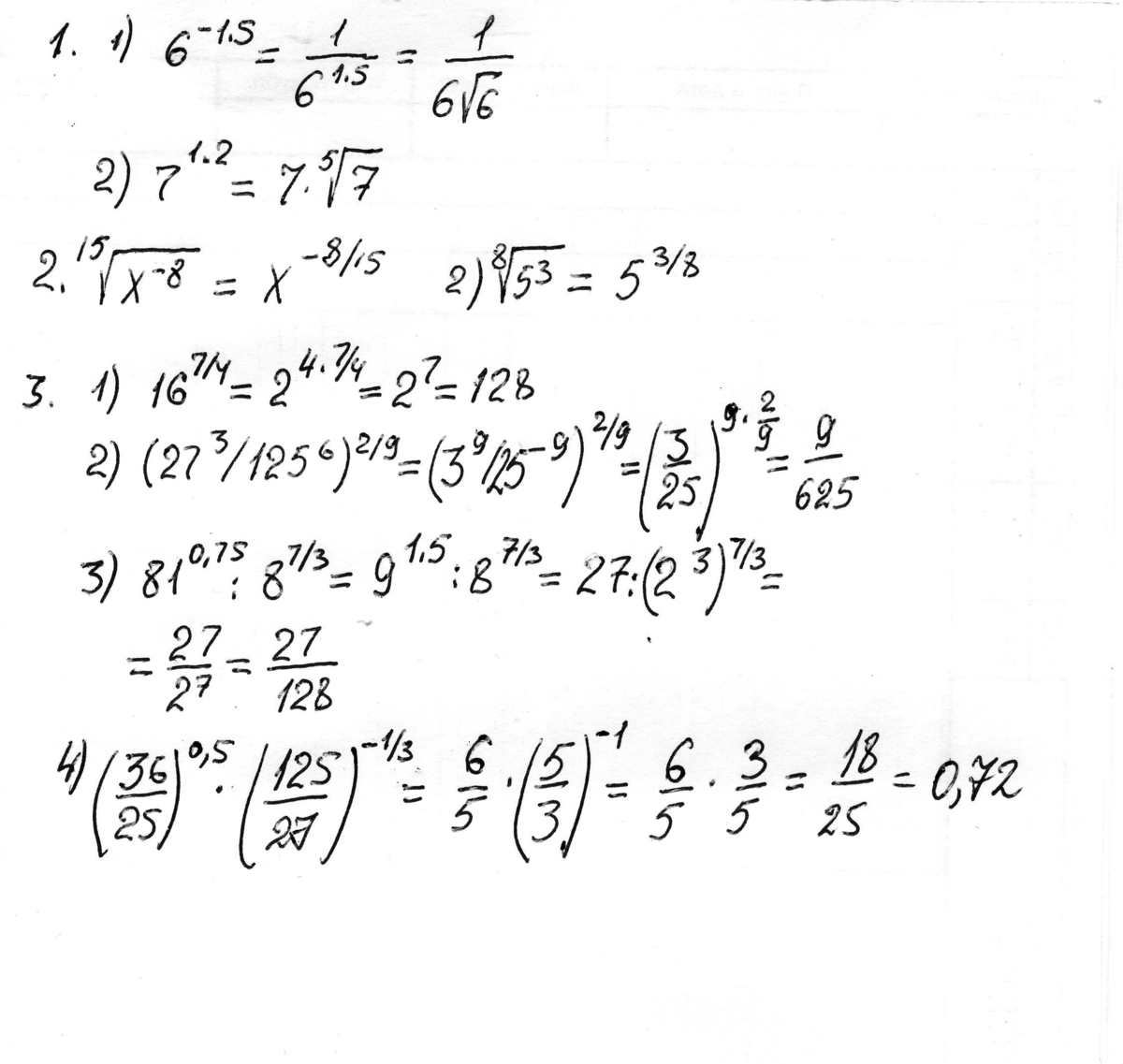
Рациональные выражения корень и степень.\( ( \frac{2}{7} +1 \frac{5}{6} )*10,5 \)
Решение: 1 целая 5/6 = 11/6 -неправильная дробь.
2/7 + 11/6 = 12/42 + 77/42 -привели к общему знаменателю = 89/42
10.5 = 10 целых 5/10 = 10 целых 1/2 = 21/2 -неправильная дробь
89/42 * 21/2 = (89/ (2*21) ) * 21/2 = 89/4 -сократили на 21
этот пример удобнее решать в обыкновенных дробях (можно сокращать.)
а 89 уже можно разделить на 4. или записать правильной дробью.
89/4 = 22 целых 1/4 (1/4 = 0.25)Понятие степени с любым рациональным показателем. a) \(\frac{a^{\frac{3}{2}}-b^{\frac{3}{2}}}{a^{\frac{1}{2}}+b^{\frac{1}{2}}}\cdot\frac{a-b}{a+a^{\frac{1}{2}}b^{\frac{1}{2}}+b} +2a^{\frac{1}{2}}b^{\frac{1}{2}}\)
b) \(\frac{a^{\frac{1}{2}}+b^{\frac{1}{2}}}{a^{\frac{1}{2}}}-\frac{a^{\frac{1}{2}}}{a^{\frac{1}{2}}-b^{\frac{1}{2}}}+\frac{b}{a-a^{\frac{1}{2}}b^{\frac{1}{2}}}\)
Решение: $$ 1)= \frac{(a^{1/2})^3-(b^{1/2})^3}{a^{1/2}+b^{1/2}}* \frac{(a^{1/2}-b^{1/2})(a^{1/2}+b^{1/2})}{a+a^{1/2}b^{1/2}+b}+2a^{1/2}b^{1/2}= \\ = \frac{(a^{1/2}-b^{1/2})(a+a^{1/2}b^{1/2}+b)}{a^{1/2}+b^{1/2}}* \frac{(a^{1/2}-b^{1/2})(a^{1/2}+b^{1/2})}{a+a^{1/2}b^{1/2}+b}+2a^{1/2}b^{1/2}= \\ =(a^{1/2}-b^{1/2})^2+2a^{1/2}b^{1/2}=a-2a^{1/2}b^{1/2}+b+2a^{1/2}b^{1/2}=a+b \\ 2)= \frac{a^{1/2}+b^{1/2}}{a^{1/2}} - \frac{a^{1/2}}{a^{1/2}-b^{1/2}}+ \frac{b}{a^{1/2}(a^{1/2}-b^{1/2})}= \\ = \frac{(a^{1/2}+b^{1/2})(a^{1/2}-b^{1/2})-a^{1/2}*a^{1/2}+b}{a^{1/2}(a^{1/2}-b^{1/2})}= \\ = \frac{a-b-a+b}{a^{1/2}(a^{1/2}-b^{1/2})} =0 $$
решить: 27в степени -2/3*9-2, тема степень с рациональным показателем.
Решение: 27 ^ ( - 2/3 ) = ( 3^3 ) ^ ( - 2/3 ) = 3 ^ ( - 2 )
9 ^ ( - 2 ) = ( 3 ^ 2) ^ ( - 2 ) = 3 ^ ( - 4 )
-
3 ^ ( - 2 ) * 3 ^ ( - 4 ) = 3 ^ ( - 2 - 4 ) = 3 ^ ( - 6 )
-
Ответ 3 ^ ( - 6 ) или 1 / ( 3 ^ 6 )Получается, что -2/3*9 = -18/3. Дальше -18/3 - 2 = -18/3 - 6/3 = -24/3 = -8 степень.
Теперь при возведении 27 в -8 степень у нас получается 1 / 27^8Степень с рациональным показателем, \(25^{ \frac{3}{2} }\); \(0,001^{- \frac{1}{3} }\); \(-27\cdot 32^{\frac{1}{5}}+13^0\); \(7-3\cdot 64^{\frac{1}{6}}\); \(3^{0,12}\cdot 9^{0,44}\); \(\frac{3^{6,2}}{9^{1,6}}\); \((27^{-\frac{2}{3}})^{-2}\); \(16^{\frac{5}{4}}-(\frac{1}{9})^{-\frac{1}{2}}+27^{\frac{2}{3}}\);
Решение: 1. $$ 25^{ \frac{3}{2} }=(5^{2})^{ \frac{3}{2} }=5^3=125 $$
2. $$ 0,001^{- \frac{1}{3} }= (\frac{1}{1000} )^{- \frac{1}{3} }= \sqrt[3]{1000} =10 $$
3. $$ -27*(2^5)^{ \frac{1}{5} }+13^0=-27*2+1=-53 $$
4. $$ 7-3*(2^6)^{ \frac{1}{6} }=7-3*2=1 $$
5. $$ 3^{0,12}*(3^2)^{0,44}=3^{0,12}*3^{0,88}=3^{0,12+0,88}=3^1=3 $$
6. $$ \frac{3^{6,2}}{(3^2)^{1,6}} = \frac{3^{6,2}}{3^{3,2}}=3^{6,2-3,2}=3^3=27 $$
7. $$ ((3^3)^{- \frac{2}{3} })^{-2}=(3^{-2})^{-2}=3^{(-2)(-2)}=3^4=81 $$
8. $$ (2^4)^{ \frac{5}{4} }-(3^{-2})^{- \frac{1}{2} }+(3^3)^{ \frac{2}{3} }=2^5-3^1+3^2=32-3+9=38 $$