свойства степеней
Решите, используя свойства степеней: \( \frac{5^7 \cdot 7^8}{35^7} \); \( \frac{2^17 \cdot 3^6}{24^5} \); \( \frac{36^7}{2^12 \cdot 3^10} \)
Решение: 1)5⁷ x 7⁸ 5⁷ x 7⁸
______ = ______ = 7¹ = 7.
35⁷ 5⁷ x 7⁷
2)
2¹⁷ x 3⁶ 2¹⁷ x 3⁶ 2¹² x 3¹ 2¹² x 3 2¹² x 3
_____ = _________ = _______ = ______ = ______ = 2² x 3 = 4 x 3 = 12.
24⁵ 2⁵ x 3⁵ x 4⁵ 4⁵ (2²)⁵ 2¹⁰
3) 36⁷ 2⁷ x 3⁷ x 6⁷ 6⁷ 2⁷ x 3⁷
_______ = _________ = _______ = ______ = 2² x 3⁴ = 4 x 81 = 324.
2¹² x 3¹⁰ 2¹² x 3¹⁰ 2⁵ x 3³ 2⁵ x 3³Найдите значение примера, используя свойства степеней \( \frac{ 9^{5} }{ 3^{7} } \), \( \frac{ 8^{7} }{ 4^{8} } \), ....
Решение: 1) \( \frac{ 9^{5} }{ 3^{7} } = \frac{ (3^{2})^5}{ 3^{7} } = \frac{ 3^{10}}{ 3^{7} } = 3^{3} =27 \)
2) \( \frac{ 8^{7} }{ 4^{8} } = \frac{ (2^{3})^7 }{ (2^{2})^8 } = \frac{ 2^{21} }{ 2^{16} } = 2^{5} = 32 \)
3) \( = \frac{ (3^{3})^3* (3^{2})^4 }{ (3^{4})^3 } = \frac{ 3^{9} * 3^{8} }{ 3^{12} } = \frac{ 3^{17} }{ 3^{12} } = 3^{5} = 243 \)
4) \( = \frac{ (5^{2})^4* (5^{3})^10 }{ 5^{36} } = \frac{ 5^{8}* 5^{30} }{ 5^{36} } = \frac{ 5^{38} }{ 5^{36} } = 5^{2} = 25 \)Пример на свойства степени \( \frac{4^{2,9} \cdot 7^{2,4}}{28^{1,4}} \)
Решение:Придется выучить эти свойства, без них вы не сможете решать задачи!
Когда основание одинаковое (то, что возводим):
1) при умножении - показатели степени складываются
2) при делении - показатели степени вычитаются
3) при возведении степени в степень (a^x)^y - основание степени остается, а показатели перемножаются: a^(x*y)
28^(1.4) = (7*4)^(1.4) = 7^(1.4) * 4^(1.4)
4^(2.9) * 7^(2.4) / 7^(1.4) * 4^(1.4) = 4^(2.9-1.4) * 7^(2.4-1.4) = 4^(1.5) * 7=7*8=56Сравнить с помощью свойств :8 в степени -0,2 и 8 в степени -1,2
Решение: Заметим, что оба числа >0, поделим одно число на другое, если результат >1, тогда числитель больше, если <1, тогда знаменатель больше, если = 1, тогда числа равны, итак:
8^-0.2 / 8^-1.2 = 8 ^(-0.2 - (-1.2)) = 8^(-0.2+1.2) = 8^1 = 8
Таким образом, 8^-0.2 больше 8^-1.2 в 8 раз
8^-0.2 > 8^-1.2
ну а свойство, которое использовали - вычитание показателей при делении чисел с одинаковым основанием.Проверьте, верны ли следующие равенства :1 в 3 степени +2 в 3 степени =(1+2)во 2 степени
1 в 3 степени +2 в 3 степени + 3 в 3 степени = (1+2+3) во 2 степени
1 в 3 степени + 2 в 3 степени + 3 в 3 степени + 4 в 3 степени = (1+2+3+4) во 2 степени
сформулируйте данное свойство чисел
проверьте это свойство для первых пяти натуральных чисел
Решение: 1) 1^3 + 2^3 = ( 1 + 2 )^2
1 + 8 = 9 ; 3^2 = 9
Равенство верное
2) 1^3 + 2^3 + 3^3 = ( 1 + 2 + 3)^2
1^3 = 1 ; 2^3 = 8 ; 3^3 = 27 ; 1 + 8 + 27 = 36
( 1 + 2 + 3 )^2 = 6^2 = 36
Равенство верное
3) 1^3 + 2^3 + 3^3 + 4^3 = ( 1 + 2 + 3 +4 )^2
4^3 = 64 ; 36 + 64 = 100
( 1 + 2 + 3 + 4)^2 = 10^2 = 100
Равенство верное
4) 1^3 + 2^3 + 3^3 + 4^3 + 5^3 = ( 1 + 2 + 3 + 4 + 5)^2
5^3 = 125 ; 100 + 125 = 225
( 1 + 2 + 3 + 4 + 5 )^2 = 225
Равенство верное
Свойство для пяти первых натуральных чисел применимо
Формулировка : сумма кубов чисел равна квадрату суммы этих чисела) X в 13 степени : X в 10 степени
б)С в 5 степени умножить с в 12 степени умножить C во 2 степени
в)y в степени 2n-3 : y в степени n+5
г)d в степени 2m умножить d в степени 0 умножить d в степени 5m-1
д)(а а в 4 степени а в 7 степени) в степени 5
е)((xв 6 степени)в 5 степени)во 2 степени
ж)(k в 4 степени)в 5 степени умножить (k во 2 степени) в 3 степени
з)(xв 4 степени) в степени m
и)125yв 3 степени
к)64
Решение: А) Х в третьей степени. При делении степени вычитаются.
б) С в 19 степени. При умножении степени складываются.
в) у в степени n-8 см. п. а
г) d в степени 7m-1
д) если два "а" в начале скобки не опечатка, то получается а в 60 степени (1+4+7=12 и умножаем на 5, т.к. степень возводится в степень)
е) Перемножаем степени и получаем х в 60 степени
ж) k в 26 степени (перемножаем, где степень возводится в степень, произведения складываем)
з) х в степени 4m (степени перемножаются, как уже было сказано выше)
и) (5у) в третьей степени, ибо 125 = 5 в кубе.
к) 8 в квадрате.Упростить \( (\frac{ \sqrt{7} }{-7} )^{-6} \)
Решение: $$ ( \frac{ \sqrt{7} }{-7} )^{-6} $$
Нам нужно сделать положительную степень,не знаю,как объяснить это правильно,но если проще,то мы переворачиваем дробь и меняем знак степени на положительный,как-то так.Например было $$ 2^{-3} $$ станет $$ \frac{1}{2 ^{3} } $$.
Получается $$ (\frac{-7}{ \sqrt{7} } )^{6} $$
На минус в числителе можно не обращать внимания,т.к степень шестая и он уберётся .
Эта степень применяется и к числителю и к знаменателю
$$ \frac{7^{6} }{ \sqrt{7 ^{6} } } $$
В знаменателе получилась такая штука $$ \sqrt{7 ^{6} } $$ это будет 7³
Получается $$ \frac{7 ^{6} }{7 ^{3} } $$
Так как основание одинаковое(и в числителе и в знаменателе 7) то при делении с одинаковым основанием показатели отнимаются,получается 7³, а это будет 343.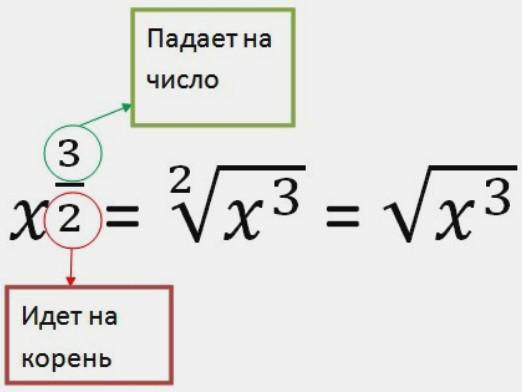
ВЫЧИСЛИТЕ: 32⁴ : (2⁴)³ · 2⁶
Решение:32⁴ : (2⁴)³ · 2⁶
пояснение: 32 =2⁵, тогда
32⁴ = 2²⁰
32⁴ : (2⁴)³ · 2⁶ = 2²⁰ · 2⁶ : 2¹²
= 2²⁶ : 2¹² =
= 2¹⁴ =
= 16384
Первый вариант:
[32⁴/(2⁴)³]*2⁶ = [(2⁵)⁴/2¹²]*2⁶ = 2²⁰*2⁶/2¹² = 2¹⁴ = 16384
Второй вариант:
32⁴/[(2⁴)³*2⁶] = 2²⁰/[2¹²*2⁶] = 2² = 4
Выберите верные равенства: А)3^2+4^2+5^2=6^2 Б)1^3+2^3+3^3+4^3=(1+2+3+4)^2 В)9^3-8^3-6^3=1^3 Г)3^3+10^3+18^3=19^2(^степень)
Решение: Б)2+8+27+64=100100=100
А)3^2+4^2+5^2=6^2
9+16+25=36
50=36-не верно
Б)1^3+2^3+3^3+4^3=(1+2+3+4)^2
1+8+27+64=100
100=100-верно
В)9^3-8^3-6^3=1^3
729-512-216=1
1=1-верно
Г)3^3+10^3+18^3=19^2
27+1000+5832=361-не верно
а) (n^8)^4:(n^4)^3 б) (t^6)^4*t в) (7^3)^8*7^5 ______________________ (t^5)^2 (7^10)^2*(7^2)^4
Решение: а) (n⁸)⁴ / (n⁴)³ = n³² / n¹² = n²⁰б) (t⁶)⁴ · t / (t⁵)² = t²⁴ · t / t¹⁰ = t²⁵ / t¹⁰ = t¹⁵
в) (7³)⁸ · 7⁵ / (7¹⁰)² · (7²)⁴ = 7²⁴ · 7⁵ / 7²⁰ · 7⁸ = 7²⁹ / 7²⁸ = 7¹ = 7
а) (n⁸)⁴ : (n⁴)³ = n³² : n¹² = n²⁰
б) (t⁶)⁴ · t : (t⁵)² = t²⁵ : t¹⁰ = t¹⁵
в) (7³)⁸ · 7⁵ : ((7¹⁰)² · (7²)⁴) = 7²⁹ : 7²⁸ = 7

