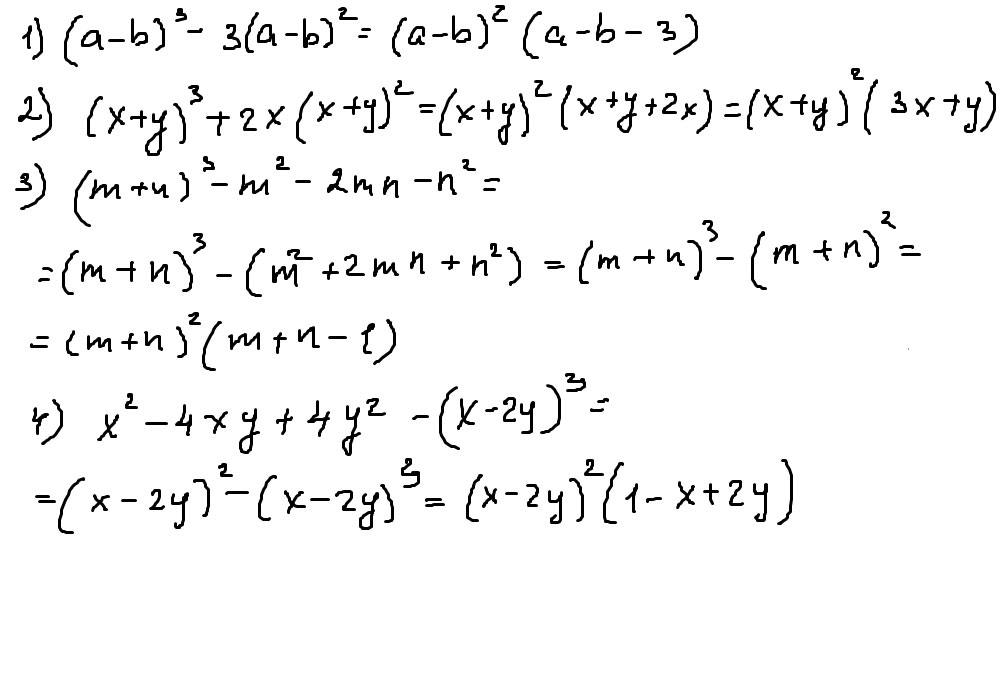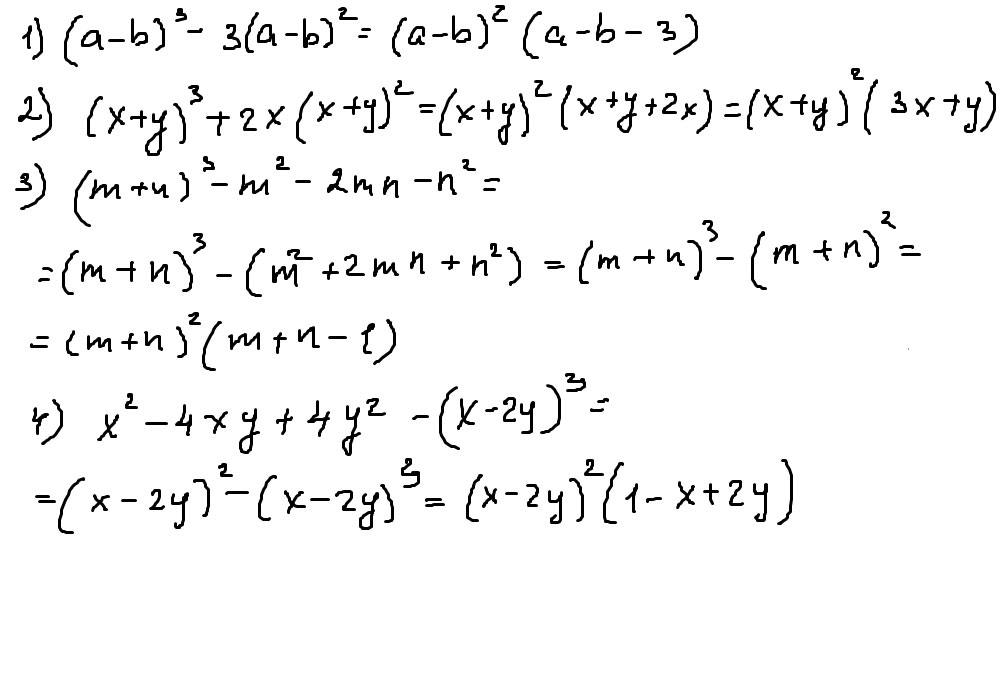степени »

представьте виде степени 10

  • 2*2^2*2^3*...*2^31 представьте произведение в виде степени


    Решение:

    2¹ * 2² * 2³ *...* 2³¹ = 2^[(1+31)*31^2] =2¹⁶*³¹ = 2⁴⁹⁶

    Показатели степени при умножении чисел с одинаковым основанием (здесь это 2) складываются. ⇒ нам надо найти сумму (S) ряда: 1+2+3+...+31
    а₁ = 1; d = а₁-а₂ = 2-1 = 1; аn = а₁ + d(n-1); n-1 = (an-a₁)/d; n-1 = (31-1)/1; n = 31;
    S = (a₁+an)*n:2 = (1+31)*31:2 = 16*31 = 496, т.е. данное произведение двоек со степенями в виде чисел натурального ряда от 1 до 31  можно представить в виде 2 в степени 496

  • Выполните деление;
    1. p^12:p^2
    2. a^16:a^7
    3. 10^21:10^12
    4. y^9:y
    5. 2,3^17:2,3^8
    6. q^12:q^8

    2. Представьте произведение в виде степени;

    1. a^3*a^4
    2. a*a^5
    3. x^5*x^3
    4. 0,5^3*0,5^7
    5. p^2*p^3
    6. q^4*q^5
    7. y^3*y^5


    Решение: При делении степени вычитаются
    1) p^12 :p^2 =p^(12-2) =p^10

    2) a^16 :a^7 =a^(16-7) =a^9

    3) 10^21 :10^12 =10^(21-12) =10^9

    4) y^9 :y =y^(9-1) =y^8

    5) 2.3^17 :2.3^8 =2.3^(17-8) =2.3^9

    6) q^12 :q^8 =q^(12-8) =q^4

    при умножении степени складываются

    1) a^3 *a^4 =a^(3+4) =a^7

    2) a*a^5 =a^(1+5) =a^6

    3) x^5 *x^3 =x^8

    4) 0.5^3 *0.5^7 =0.5^10

    5) p^2 *p^3 =p^5

    6) q^4 *q^5 =q^9

    7) y^3 *y^5 =y^8

  • Представьте произведение (-x) (-x) (-x) (-x) (-x) (-x) в виде степени


    Решение: Х в 6 степени 
    так как минус ну минус дает плюс, плюс на минус дает минус, их четное число и по этому число положительное

    Чтобы представить в виде степени нужно это число возвести в число сколько раз оно умножается: (-x)в шестой степени, но возводиться в четную степень то равно x в шестой степени

  • Представьте степень натурального числа в виде произведения:76 в третьей степени?


    Решение: Чтобы возвести в степень произведение, достаточно возвести в эту степень каждый сомножитель и результаты перемножить, то есть(а • b)^n = (a^n)*(b^n).
    Исходное выражение (0,5x⁴4y⁻³)⁻² - произведение.
    0,5 можно сразу умножить на 4, тогда получаем:
    (2x⁴y⁻³)⁻² = 2⁻²x⁻⁸y⁶ = 0,25x⁻⁸y⁶.

  • Представьте в виде произведения: 1) (a-b)^3 - 3(a-b)^2
    2) (x+y)^3 + 2x(x+y)^2
    3) (m+n)^3 - m^2 - 2mn - n^2
    4) x^2 - 4xy + 4y^2 - (x-2y)^2
    ^ - в степени....


    Решение: 1) (a - b)³ - 3(a - b)² =  (a - b)² * (a - b) - 3(a - b)² = (a - b)² * (a - b - 3)
    2) (x + y)³ + 2x(x + y)² = (x + y)² * (x + y) + 2x(x + y)²  = (x + y)² (3x + y)
    3) (m + n)³ - m² - 2mn - n² =  (m + n)³ - (m + n)² =  (m + n)² * (m +n) - (m + n)²  = (m + n)² (m + n -1)
    4) x² - 4xy + 4y² - (x - 2y)² = (x - 2y)² - (x - 2y)²  = 0 a - b - a - b    a - b   a - b - a - b a - b a - b - x   y x x   y   x   y x y   x x   y   x y x y m   n - m - mn - n    m   n - m  n    m   n m n - m  n   m n m n - x - xy y...

  • Представьте в виде произведения 14x+21y; 15a+10b; 8ab-6ac; 9xa+9xb; 6ab-3a; 4x-12x во 2й степени; m в 4й степени -m во 2й степени; c в 3й степени+c в 4й степени; 7x-14x в 3й степени; 16y в 3й степени+12y во 2й степени; 18ab в 3й степени-9b в 4й степени;


    Решение: 7(2х+3у)

    5(3а+2в)

    2а(4в-3с)

    9х(а+в)

    3а(2в-1)

    4х(1-3х)

    m^2(m^2-1)=m^2(m-1)(m+1)

    c^3(1+c)

    7x(1-2x^2)

    4y^2(4y+3)

    9b^3(2a-b)

    14х+21у=7(2х+3у)

    15а+10в=5(3а+2в)

     8ав-6ас=2а(4в-3с)

    9ха+9хв=9х(а+в)

    6ав-3а=3а(2в-1)

    4х-12х²=4х(1-3х)

    m⁴-m²=m²(m²-1)=m²(m-1)(m+1)²

    c³+c⁴=c³(1+c)

    7x-14x³=7x(1-2x²)

    16y³+12y²=4y²(4y+3)

    18ab³-9b⁴=9b³(2a-b)

  • Представьте в виде степени и вычислите 2^17^*2^-15^*2^2


    Решение: Свойство степени- a^m * a^n= a^m+n
    при умножении степеней с одинаковым основанием показатели степени складываются, а показатель остается прежним. 
    а при делении, кстати, степени вычитаются.
     ТАК ВОТ
    2^17-15+2= 2^4= 16
    T_T

    Решение:
    2^17*2^-15*2^2=2^(17-15+2)=2^4=16

    Ответ:16

  • Представьте:в) в виде степени десяти число: 10000000;100;1000000;100000

    Представьте:
    г) в виде степени пяти число: 625;25;125


    Решение:  в) 10000000 - это 10 в 7 степени; 100-это 10 во 2 степени или в квадрате; 1000000 - это 10 в 6 степени; 100000 - 10 в 5 степени. Степень - это произведение равных множителей, поэтому для 10 сколько нулей столько и показатель степени. 1000=10х10х10 или 10 в кубе или в 3-й степени.
    г) 25=5х5 или 5 во 2-й степени; 125=5х5х5 или 5 в 3-й степени; 625=5х5х5х5 или 5 в 4-й степени.

  • Представьте: б) в виде куба число: 64; - 216; 0,008; - 1|64; 4 17|27 в) в виде степени десяти число: 10; 100; 1000; 1000000 г) в виде степени пятичисло: 125; 625; 15 625


    Решение: б) 64/ 4) -216/ -6) 0,008/ 0,2)

    4*4*4(4 в кубе)=64

    6*6*6(6 в кубе)=216

    0,2*0,2*0,2(0,2 в кубе)=0,008

    -1/4*-1,4*-1,4(-1/4 в кубе)=-1/64

    5/3*5/3*5/3(5/3 в кубе)=4 17/27

    10*1(10 в 1 степени)=10

    10*10(10 в квадрате)=100

    10*10*10(10 в кубе)=1000

    10*10*10*10*10*10(10 в 6 степени)=1000000

    5*5*5(5 в кубе)=125

    5*5*5*5(5 в 4 степени)=625

    5*5*5*5*5*5(5 в 6 степени)=15625

  • Представьте данное число в виде степени какого-либо числа с показателем отличным от 1: а) 243; б) 0,125 в) -216/343 г) 1000; д) 243/32 е)1 000 000; ж) 27 з) 10 000 и) 512


    Решение: а)243=(3)в 5 степени

    б)0,125=(0,005)в 3 степени

    в)???

    г)1000=10 в 3 степени

    д)???

    е)1 000 000 =10 в 6 

    ж)27=3 в 3 

    з)10 000=10 в 4

    и)512=8 в 3

    а) 243=3⁵,

    б) 0,125=0,5³,

    в)-216/343=-6³/7³=-(6/7)³,

    г) 100010³;

    д)243/32=3⁵/2⁵=(3/2)⁵,

    е)1 000 000=10⁶;

    ж)27=3³,

    з)10 000=10⁴,

    и)512=2⁹.