преобразуйте в дробь выражение
6. преобразуйте в произведение выражение cos9x –cos13x –sin2x
7. сократите дробь ( cos9α + cos7α ) / (cos6α cos2α - sin6α sin2α)
8. докажите тождество 2/(1- sin2α) = 1 + ctg2(α -π/4)
Решение:6 превратить в произведение
Cos9x – cos13x – sin2x = ( Cos9x – cos13x ) – sin2x =
= - 2*sin [(9x+13x)/2]* sin [(9x-13x)/2] - sin2x =
= -2*sin11x *sin(-2x) - sin2x = 2*sin11x * -sin(-2x) - sin2x = **-sin(-2x)=sin2x
= 2*sin11x * sin2x - sin2x = sin2x * (2*sin11x - 1)
7 Сократите
(Cos9a +cos7a ) / (cos6a*cos2a – sin6a*sin2a)
Преобразуем по частям
Числитель - переход от суммы к произведению
Cos9a +cos7a = 2*cos[(9a+7a)/2 ]* cos[(9a-7a)/2 ]=2*cos8a*cosa (1)
Знаменатель - формула сложения
cos6a*cos2a – sin6a*sin2a=cos (6a +2a) =cos 8a (2)
подставим части в дробь
(1) / (2) = 2*cos8a*cosa / cos 8a = 2 cos a
8 доказать тождество
2/ (1-sin2a) =1+ctg2 (a –п/4)
Преобразуем по частям
Левая часть
2/ (1-sin2a) = 2/ (1-2sinα*cosα)= 2/ (sin2α +cos2α -2sinα*cosα)=2/( sinα-cosα)2
Правая часть
1+ctg2 (a –п/4)=1/sin2(a-п/4)=1/(sina*cos п/4 –sin п/4*cosa)2=
=1/ (sina * 2/√2 - 2/√2 *cosa)2 =1/ (4/2 *( sinα-cosα)2) =2/( sinα-cosα)2
2/( sinα-cosα)2 =2/( sinα-cosα)2
В обеих частях одно и то же выражение
Доказано

1) Преобразуйте данное выражение в многочлен:
а) (а+1)(а^2-а+1)=
б)(b-2)(b^2+2b+4)=
в) (3x+2)(9x^2-6x+4)=
г) (3-5y)(9+15y+25y^2)
д) (2-n^4)(4+2n^4+n^8)=
е)(a+b^2)(a^2-ab^2+b^4)=
2) Упростите выражение и найдите его значение:
а) (4x-3)(16x^2+12x+9)-9(x^3-3) при х= 1/5
б) x(x^2-4x)-(x-3)(x^2+3x+9) при х=1/2
в) (2y+x^2)(4y^2-2x^2y+x^4)-(x^3+y)(x^3-1) при х=1, у= -1
Решение: 1) Преобразуйте данное выражение в многочлен:
а) (а+1)(а^2-а+1)=a³+1
б)(b-2)(b^2+2b+4)=b³-8
в) (3x+2)(9x^2-6x+4)=27x³+8
г) (3-5y)(9+15y+25y^2)=27-125y³
д) (2-n^4)(4+2n^4+n^8)=8-n^12
е)(a+b^2)(a^2-ab^2+b^4)=a³+b^6
2) Упростите выражение и найдите его значение:
а) (4x-3)(16x^2+12x+9)-9(x^3-3) при х= 1/5
64x³-27-9x³+27=55x³ 55/125=11/25
б) x(x^2-4x)-(x-3)(x^2+3x+9) при х=1/2
x³-4x²-x³+27=27-4x² 27-4*1/4=26
в) (2y+x^2)(4y^2-2x^2y+x^4)-(x^3+y)(x^3-1) при х=1, у= -1
8y³+x^6-x^6-yx^3+x^3+y -8+1-1+1+1-1=-7
(2y+x^2)(4y^2-2x^2y+x^4)-(x^3+1)(x^3-1) при х=1, у= -1
8y³+x^6-x^6+1=8y³+1 -8+1-7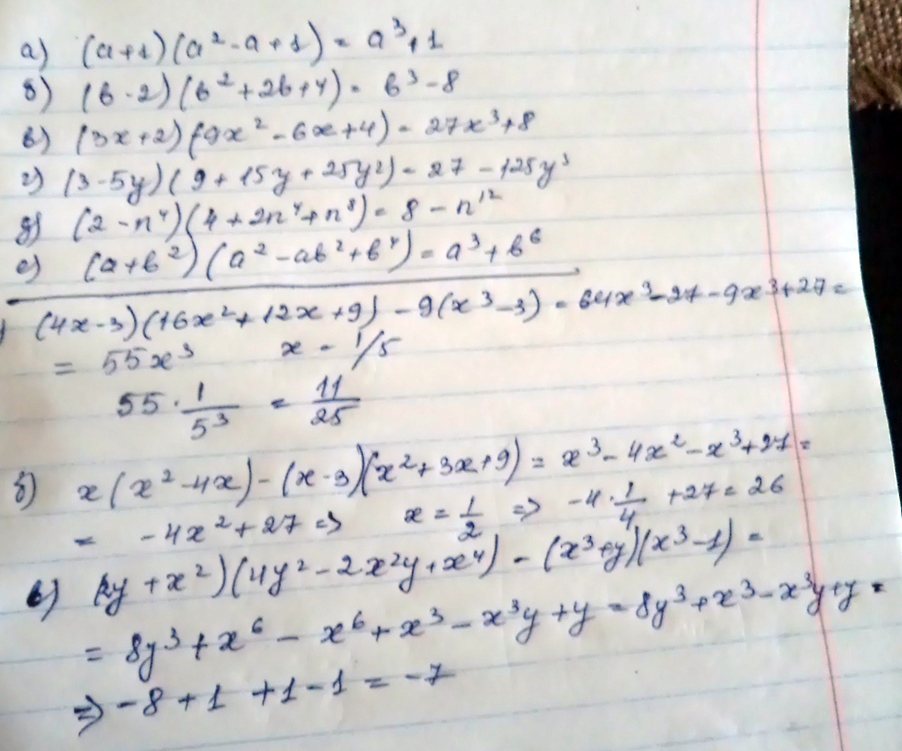
Преобразуйте в многочлен выражение :
(a+b)^2(a-b)
сократите дробь:
\( \frac{x^{2}-25}{x^{2}-3x-10} \)
Решение: По формуле квадрат суммы в первом множителе получаем (а^2+2ab+b^2)(a-b)=a^3+2a^2 b+ab^2-ba^2-2ab^2-b^2=a^3-b^3-ab^2+ba^2
сократить дробь:
числитель х^2 -25= (x-5)(x+5)
знаменатель приравнять к нулю и решить по дискриминанту, получим х1=5, х2=-2
то есть знаменатель можно представить в виде произведения (х-5)(х+2)
теперь сокращаем одинаковые скобки в числителе и знаменателе:
(х+5)/(x+2)

1. Найдите значение выражения
0,2^2-2*0.06+0.3^2
-= ?
0.2*0.9-0.5
- это деление
2. преобразуйте в многочлен выражеие:
2(u-3)u-(u-3)(u+3)
3. Сократите дробь:
X^16-X^8+1
-=?
X^24+1
Решение: X^16-X^8+1 X^16-X^8+1 1
- =- =-
X^24+1 (X^8+1)(X^16-X^8+1) (X^8+1)
0,2^2-2*0.06+0.3^2 (0.2-0.3)² 0.01 1
- =- = - = -
0.2*0.9-0.5 -0.32 -0.32 321. 0,82:(-0.32)=-2,5625
2.(u-3)^2
3. х+1
-
х^3
1. Упростите выражение и найдите его значение.
(2а-б)(4а в квадрате + 2аб+б в квадрате )
при а= -2
при б = дробь : одна двести первая
2. Преобразуйте в многочлен стандартного вида.
(3а-2)(3а+2)+(2а-3) в квадрате.
3. Решите уравнение.
(2х +3) в квадрате-7=(2х-1)(2х+1)
Решение: Упрастим получится 2а в кубе +б в кубе. теперь представляем 2*(-2) в кубе + 1/201 в кубе =-16 + 1/8120601=-12992916/8120601+1/8120601=-129929616/8120601=-16 Это первое задание3. Решите уравнение.
(2х +3)²-7=(2х-1)(2х+1)
4x²+12x+9-7=4x²+2x-2x-1
12x=-1+7-9
12x=-3
x=-3/12=-1/4
2)(3а-2)(3а+2)+(2а-3)²=9a²+6a-6a-4+4a²-12a+9=13a²-12a+5


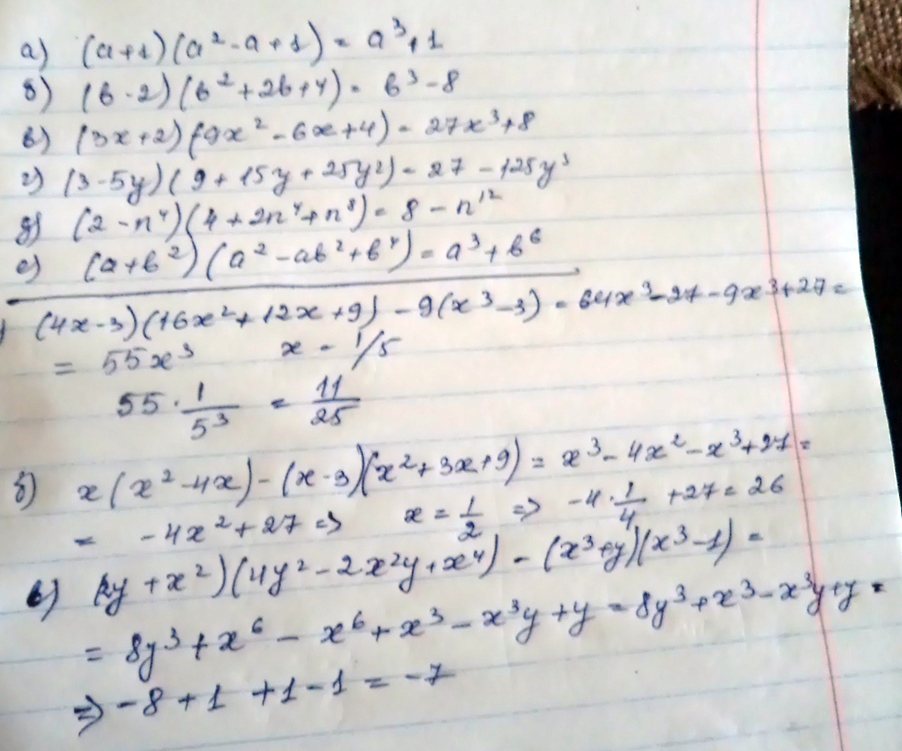

 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...