дроби »
преобразуйте в дробь выражение - страница 2
В первом сократить дроби, во втором преобразовать в дробь выражения, в третьем упростить выражение, а в четвертом найти допустимые значения перемен ной в выражении
Решение: 1в)$$ \frac{a+1}{ a^{2}+2a+1 } = \frac{a+1}{(a+1) ^{2} } = \frac{1}{a+1} $$
2а) (a+4)/4a-(a-2)/a^2=(a^2+4a-4a+8)/4a^2=a^2+8/4a^2
б) 3х/(х+3)+3х/(х-3)=(3х^2-9x+3x^2+9x)/(x+3)(x-3)=6x^2/(x^2-9)
в) 9x^2/(3xy-y^2)-y/3x-y=(9x^2-y^2-x^2-9)/(3xy-y^2)=(3x-y)(3x+y)/y(3x-y)=(3x+y)/y
г) a-3b+6ab/a-3b=a^2-3ab-3ab+9b^2+6ab/a-3b=a^2+9b^2/a-3b=(a+3b)(a-3b)/a-3b=a+3b
3) 1/(x+2)+2/(x^2-2x)-4/(4-x^2)=x^2-2x+2x+4+4x/(x-2)(x+2)x=x^2+4x+4/(x-2)(x+2)x=(x+2)^2/(x-2)(x+2)x=x+2/(x-2)xПреобразуйте в дробь выражение:
\( \frac{m}{1} + \frac{1}{n} \)
Решение: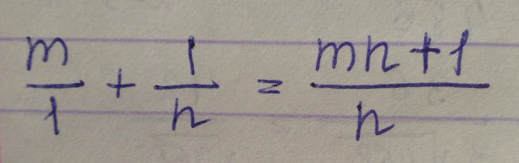
Преобразуйте дробь в выражение a^2-a/a^3+1 - 1/1+a
Решение: Сначала у первой дроби знаменатель расписываем по формуле сумма кубов. Далее приводим всё к общему знаменателю, для этого домножим вторую дробь на (а^2 - а + 1). Все ’а’ в числителе посокращались. Ну и последним действием свернули знаменатель по формуле сумма кубов.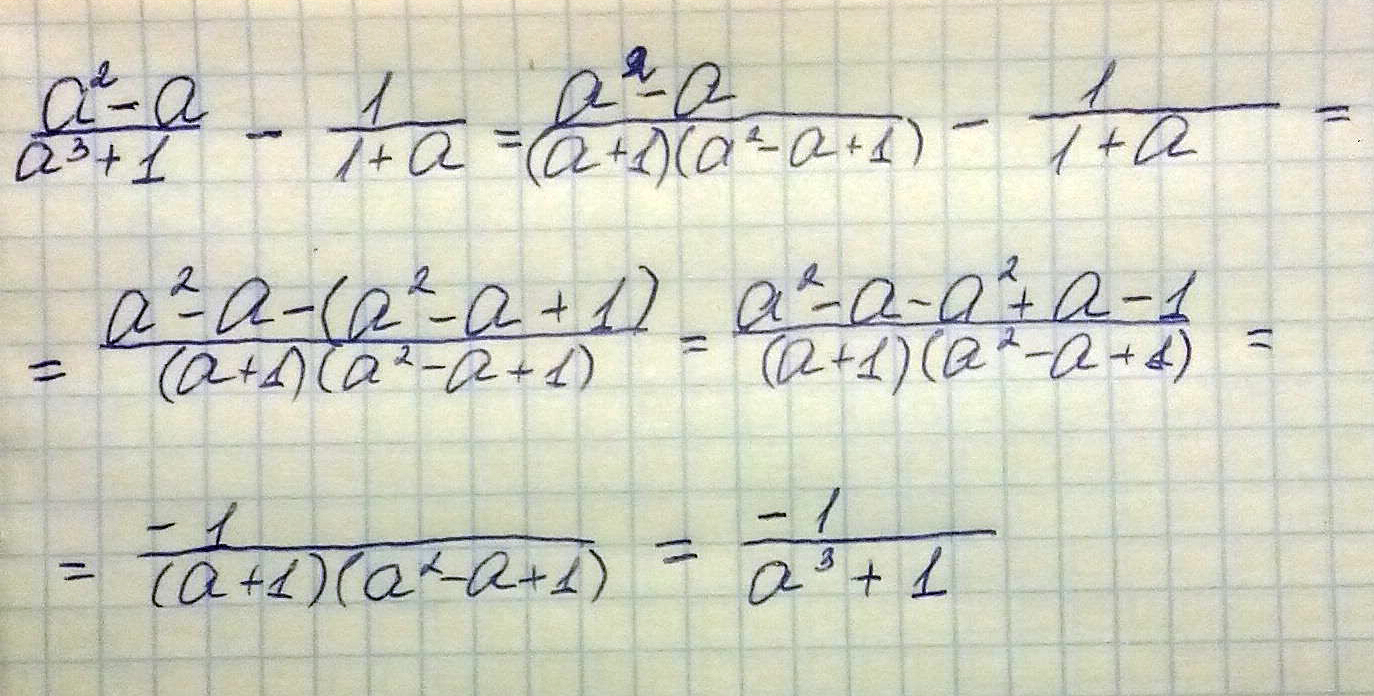
Помогите преобразуйте в дробь выражение \(\frac{2}{(x-2)^2} + \frac{2}{4-x^2}+\frac{1}{x^2+2x} \)
Решение: $$ \frac{2}{(x-2)^2}- \frac{2}{(x-2)(x+2)} + \frac{1}{x(x+2)} = \frac{2x^2+4x-2x^2+4x+x^2-4x+4}{x(x-2)^2(x+2)} = \frac{x^2+4x+4}{x(x-2)^2(x+2)}= \\ = \frac{(x+2)^2}{x(x-2)^2(x+2)} = \frac{x+2}{x(x-2)^2} $$Во вложении
__________________________________________________
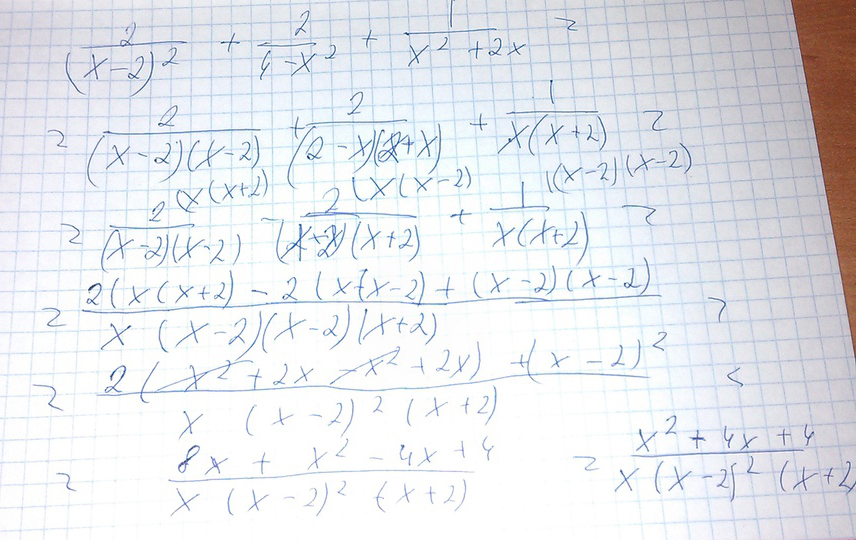
преобразуйте в дробь выражения:
а) x+2/x+3 - x-1/x
б)2y- 4y²/2y-1 -1
в)5a²/5ab-b² - b/25a-5b
г)x²/x³-x + 1/2-2x
Решение: а)x+2/x+3 - x-1/x=
=2/x+3-1/x=
=3+1/x=(3x+1)/x
б)
2y- 4y²/2y-1 -1=
=2y-2y-2=-2
в)
5a²/5ab-b² - b/25a-5b=
=5a²/(b(5a-b)) - b/(5(5a-b))=
=(25a^2 -b^2)/(5b(5a-b))=
=(5a -b)(5a+b)/(5b(5a-b))=
=(5a+b)/(5b)
г)
x²/x³-x + 1/2-2x =
=x^2/(x^3-x) + 1/(2-2x)=
=x/(x^2-1) + 1/(2*(1-x))=
=x/(x^2-1) - 1/(2*(x-1))=
=(2x-(x+1)/(2(x^2-1))=
=(x+1)/(2(x^2-1))=
=1/(2(x+1))

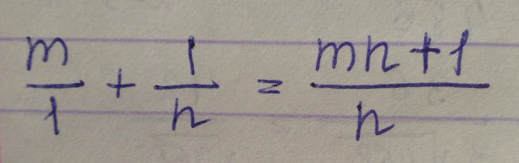
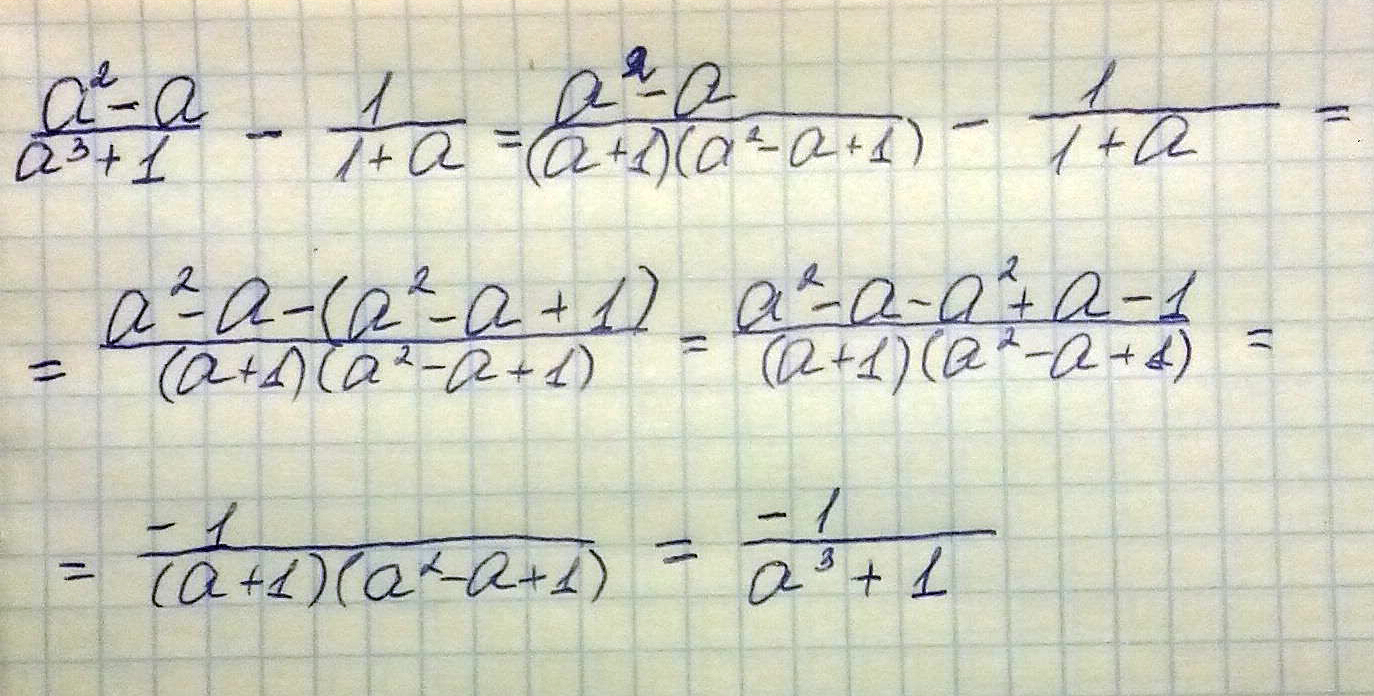
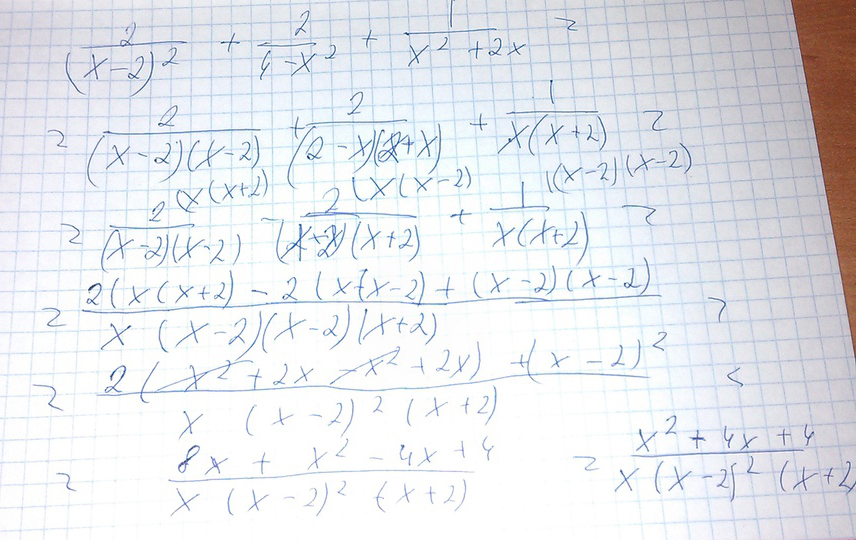
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...