дроби »
вычитание дробей с разными
Объясните сложение, вычитание дробей с разными знаками.
Решение: Например 24|6 - 9|24. Первое действие - находим общий знаменатель для чисел 6 и 24. Общим знаметелем для них является чило 24, так как оно делится и на 6, и на 24. 2-ое действие - разделмв 24 на шесть. Мы получаем ответ 4, разделив 24 на 24, мы получаем ответ 1. Теперь ответ 4, полученный при делении 24|6, умножаем на 24, получаем 96.
Полученный ответ, при делении 24|24=1, умножаем на 9, получаес 9. Отнимаем тба числа, получаес новую дробь. Отнимаем 96-9|24=83|24.
Со сложением Тоже самое, вместо минуса будет плюс!Сложение и вычитание дробей с разными знаменателями.
Объясните как делать пример и решите его: \( \frac{3b + 7}{3b} - \frac{b^{2} - 5}{b^{2} } \)
Решение: Сначала приводим к общему знаменателю и вычисляем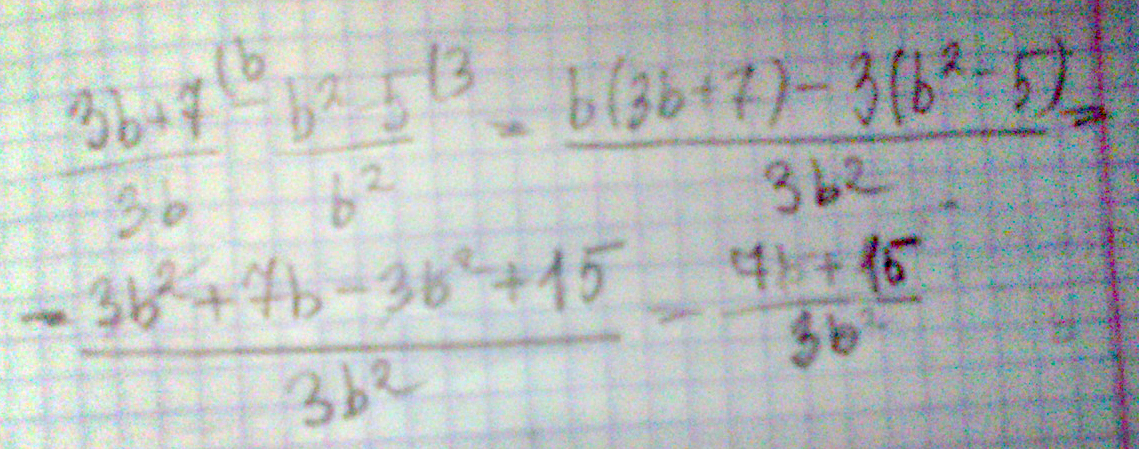
Тема "Сложение и вычитание дробей с разными знаменателями (знаменатели - произвольные)
Решение: 1) В первом случае у первого знаменатель 4a, а у второго 8а². Надо приводить к общему знаменателю, значит надо первую дробь домножить на 2a, чтобы получить 8а². Не забываем, что если при раскрытии скобок перед ней стоит "-", то знаки в скобке меняем. Получаем:
$$ \frac{2a(2a-1) -3a-2}{8a^2}= \frac{4a^2 - 2a - 3a -2}{8a^2}= \frac{4a^2-5a-2}{8a^2} $$
2) Делаем тоже самое: приводим к общему знаменателю. В первом 5-m, во втором m-5. Во втором случае надо вынести за скобку минус, получим: - (5-m). Минус поднимается вверх и встает перед скобкой, замещая плюс. Получаем:
$$ \frac{6-m-m-4}{5-m}= \frac{2-2m}{5-m} $$Тема: Сравнение, сложение и вычитание дробей с разными знаменателями
№1
сахар высыпали в два пакета. в первый пакет высыпали 5/8 кг, а во второй- на 1/4 кг больше. какова масса всего сахара?
№2
вычислите:
а)4/25+0,8-2/3
б)3/14+(11/63-5/42)
№3
Решите уравнение:
19/21-х=3/7+1/14
Решение: №1.
1) 5/8 + 1/4 = 5/8 + (1*2)/(4*2) = (5+2)/8 = 7/8 (кг) сахара высыпали во второй пакет.
2) 5/8 +7/8 = (5+7)/8 = 12/8 = 3/2 = 1 1/2 = 1,5 (кг)
Ответ: 1,5 кг масса всего сахара.
№2.
а) 4/25 + 0,8 - 2/3 =
можно привести все дроби к одинаковому знаменателю:
= 4/25 + 8/10 - 2/3 = (4*6)/(25*6) + (8*15)/(10*15) - (2*50)/(3*50)=
= (24+120 - 100)/150 = 44/150 =22/75
или решить по действиям:
1) 4/25 + 0,8 = 0,16 +0,8 = 0,96
2) 0,96 - 2/3 = 96/100 - 2/3 =
= 24/25 - 2/3 = (24*3)/(25*3) - (2*25)/(3*25) =
= (72-50)/ 75 = 22/75
б) 3/14 + (11/63 - 5/42 ) =
= 3/14 + 11/63 - 5/42 = (3*9)/(14*9) + (11*2)/(63*2) - (5*3)/(42*3) =
= (27+22-15)/126 = 34/126 = 17/63
по действиям:
1) 11/63 - 5/42 = (11*2)/(63*2) - (5*3)/(42*3) = (22-15) /126= 7/126= 1/18
2) 3/14 + 1/18 = (3*9)/(14*9) + (1*7)/(18*7) = (27+7)/126= 34/126= 17/63
№3.
19/21 - х = 3/7 + 1/14
19/21 - х = 6/14 + 1/14
19/21 - х = 7/14
19/21 - х = 1/2
х= 19/21 - 1/2 = 38/42 - 21/42
х= 17/42
19/21 - 17/42 = 3/7 + 1/14
38/42 - 17/42 = 6/14 + 1/14
21/42 = 7/14
1/2 = 1/2Найдите значение выражения 3/4 + 3/14 (тема: сложение и вычитание дробей с разными знаменателями
Решение: 1) Находим НОК чисел 14 и 4. (НОК (14, 4)=28)
2) Перемножаем дробь на такое число чтобы получилось 28 в знаменателе.
И получаем ответ: 27/28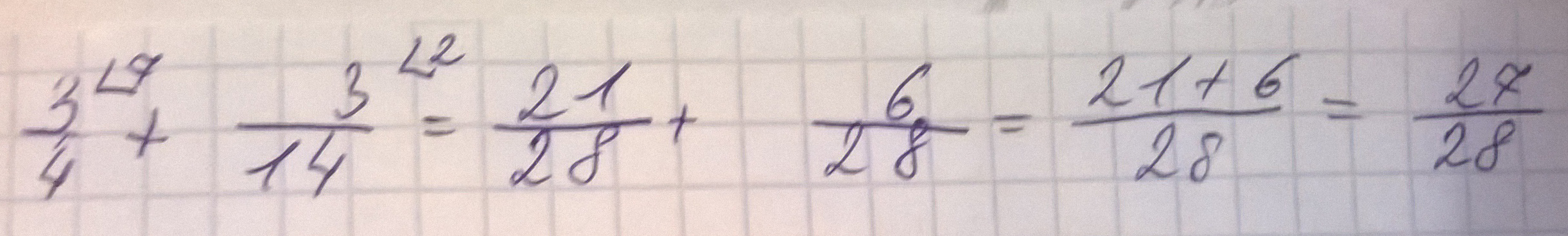

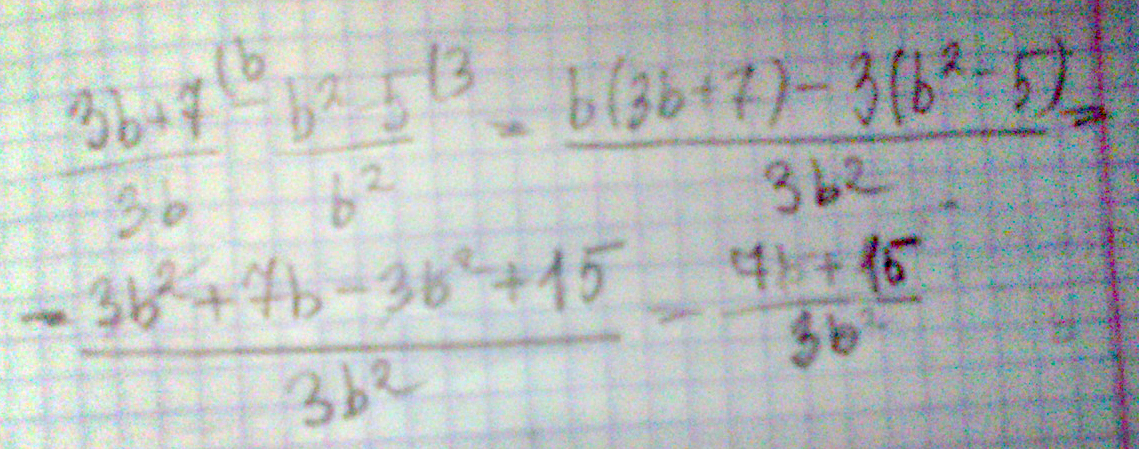
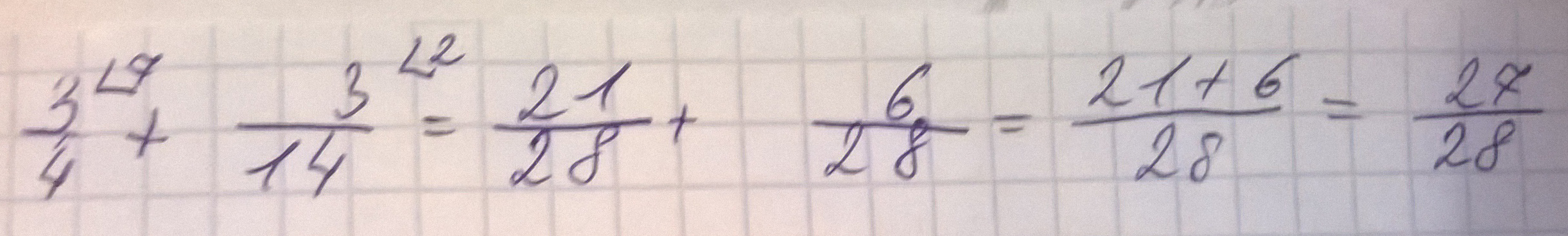
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...