при каких значениях переменной дробь имеет значение - страница 2

Исполнитель Чертежник перемещается на координатной плоскости, оставляя след в виде линии. Чертежник может выполнять команду Сместиться на (a, b) (где a, b — целые числа), перемещаю- щую Чертежника из точки с координатами (x, y) в точку с координатами (x + a, y + b). Если чис- ла a, b положительные, значение соответствующей координаты увеличивается, если отрицательные — уменьшается. Например, если Чертежник находится в точке с координатами (5, 3), то команда Сместиться на (2, –3) переместит Чертежника в точку (7, 0). Запись Повтори k раз Команда 1, Команда 2, Команда 3 конец означает, что последовательность команд Команда 1, Команда 2, Команда 3 повторится k раз. Чертежнику был дан для исполнения следующий алгоритм: Повтори 4 раза Сместиться на (2, 0), Сместиться на (0, 3), Сместиться на (–2, –3) конец Какую фигуру нарисует Чертежник? 1) треугольник 2) квадрат 3) незамкнутую ломаную линию 4) параллелограмм

рисуете обычную сетку координат х и у, начинаете с точки (0, 0), т.е. вот так по координатам (х,у) ставите в ней точку, далее смотрим на условие:
 1) 4 раза Сместиться на (2, 0), следовательно получаем последовательно 4 точки: (2, 0), (4,0), (6,0) (8,0), т.е. к х прибавляем х, к у прибавляем у и получаем точки, конечную точку фиксируем на графике ( было х=0 и у=0, в конце получаем что х= 4*(х+2) и у=4*(0+0), умножаем на 4 потому, что в условии написано "4 раза сместиться на (2,0) )

2) Сместиться на (0, 3),  следовательно делаем то же самое: из точки (8,0) перемещаемся в точку (8,3), получается что теперь х = 8+0, а у=0+3)

3)Сместиться на (–2, –3),  так же: из точки (8;3) в точку (6;0), так как х=8-2, а у=3-3

в итоге получается треугольник:)

Преобразуйте выражения в многочлен:
а) (2х - 5) (2х + 5);
б) (3-4х)^2
в)(х+4)^3
г)(х-6+у)^2
д) (3х-2) (9х^2+6х+4)
Номер 2:
Разложите на множители: а) 8х^2 - 8у^2; б) 2а^2 + 8ав +дв^2; в) а^4 -1
Номер 3:
При каких значениях переменной значения выражений х(х+2) и (х-4) (х+4) равны?
Номер 4:
Решите уравнения, используя разложение на множители многочленов:
а) 9х^3 - х = 0
б) 5х^2 - 10х + 5 = 0

 б) 2х2 – 20х + 50 =2(x^2-10x+25)=2(x-5)^2=2(x-5)(x+5)
 3. Найдите значение выражения а2 – 4bс=36-4*(-11)*(-10)=36-440=-404
 а) 452 б) -202 в) -404 г) 476 
4. Упростите выражение: 
 (с2 – b)2 – (с2 - 1)(с2 + 1) + 2bс2 =c^4-4bc^2+b^2-c^4+1=-4bc^2+b^2+1
5. Докажите тождество: 
(а + b)2 – (а – b)2 = 4аb

a^2+2ab+b^2-a^2+2ab-b^2=2a+2ab=4ab

второй 1)x²- 4=(х+2)(х-2) т. к 2 в квадрате равно 4

2)x²- 3=(х+)(х-)

3) не раскладывается т. к там сумма

4)a²- 4=(а+2)(а-2)

5)a - 9=(корень из а +3)(корень из а -3)

6)x² - x=(х+корень из х)(х-корень из х)

7)u - 3=(корень из u+)(корень из u-)

8) не раскладывается

9)7 - a⁴=(+a²)(-a²)

третий 

x(x+2)=(x-4)(x+4)
x^2 + 2x = x^2 - 16
x^2 - x^2 + 2x = -16
2x = -16
x = -8

четвертый

полный квадрат:

x^2-9x+14=x^2-2*4,5x+20,25-20,25+14=(x-4,5)^2-6,25=(x-4,5-2,5)(x-4,5+2,5)=(x-7)(x-2)=0

x=7 или x=2

x^2-5x-14=x^2-2*2,5x+6,25-6,25-14=(x-2,5)^2-20,25=(x-2,5-4,5)(x-2,5+4,5)=(x-7)(x+2)=0

x=7 или x=-2

разложение на множетели:

x^2-9x+14=x^2-7x-2x+14=x(x-7)-2(x-7)=(x-7)(x-2)=0

x=7 или x=2

x^2-5x-14=x^2-7x+2x-14=x(x-7)+2(x-7)=(x-7)(x+2)=0

x=7 или x=-2

1) в каждой паре чисел большего модуля вычтиите меньший модуль.
-0,8 и 4 ___
0.9 и -0.99 ___
1\4 и 2целых 3\4 ___
2) При каких значениях переменной верно каждое равенство:
" (X) - ()-скобки модуля "
(X) = 12 ___________
(Y) = -1 ___________
(А) = 3.4 ___________
(С) = 0 ______________
3) При холодном способе засолки грибов норма соли составляет 4.5% массы грибов. Рассчитайте количество соли, необходимое для засолки 2.5 кг грибов.
Решение:________________________
__________________________________
__________________________________
Ответ: ______________
4) Ширина прямоугольного участка земли 15 м, а длина 20 м. Найдите отношение ширины к длине и выразите его в процентах.
Решение: _________________________
__________________________________
_________________________________
Ответ: ____________
5) Ширина прямоугольника 8 дм. Она составляет 20% его длины. Чему ровна площадь этого прямоугольника?
Решение: ____________________________
_________________________________-
_________________________________-
Ответ: _____________
6) У пети 100 руб. У Феди на 20% денег больше чем у Пети, а у кати на 20% больше чем у феди. сколько рублей у Кати?
Решение: _________________
_____________________
____________________
Ответ: ____________________
7) Выполните действия:
0.125 + 1\8 =
0.125 - 1\8 =
0.125 * 1\8 =
0.125 : 1\8 =

Приведите многочлен к стандартному виду и выясните, при каких значениях переменной его значение равно 1:
а) x^3+2x^2+7x+8x-x^3-x^2-x^2
б) 0,5y^3+2,7y^2+3,5y+6,5y-0,5y^3-2y^2-0,7y^2
в) 3z^4-z^2+4z+z+z^2-2z^4-z^4+8
г) 6p^3-p^2+4p^3+p^2-10p^3-3p+19

если переменная равна 1, то 15*1=15

б) 0,5y^3+2,7y^2+3,5y+6,5y-0,5y^3-2y^2-0,7y^2=10y
 если переменная равна 1, то 10*1=10
  в) 3z^4-z^2+4z+z+z^2-2z^4-z^4+8=5z+8

если переменная равна 1, то 5z+8=13
 г) 6p^3-p^2+4p^3+p^2-10p^3-3p+19=19-3p
 если переменная равна 1, то 19-3p=16

№1
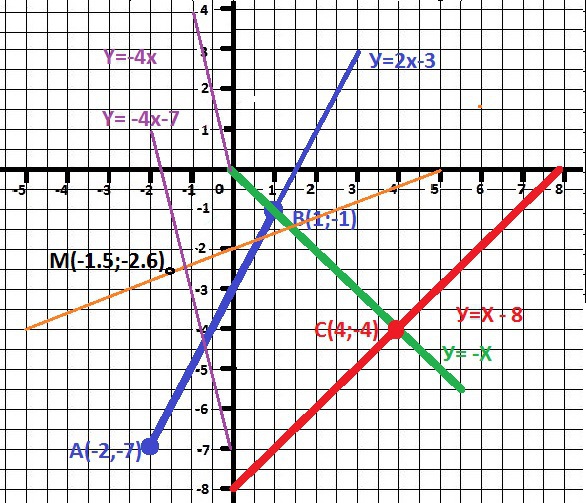
постройте график линейной функции y=2x-3
С помощью графика найдите:
a) наименьшее и наибольшее значения финкции на отрезке [-2;1]
б) значение переменной x при которых график функциирасположен выше оси Ox
№2
найдите координаты точки пересечения прямых y=-x и y=x-8
№3
а) найдите координаты точек пересечения графика линейного уравнения 2x-5y-10=0 c осями координат
б) определите принадлежит ли графику данного уравнения точка М (-одна целая одна вторая; -2,6)
№4
а) задайте линейную функцию y=kx формулой, если известно что ее график параллелен прямой 4x+y+7=0
б) определите, возрастает или убывает заданная вами линейная функция
№5
при каком значении p решением уравнения:
-px+2y+p=0
является пара чисел (-1;2)