сокращение дробей
СОКРАЩЕНИЕ ДРОБЕЙ. Объясните как сокращать дроби, в которых как бы числитель умножен на число и знаменатель. В учебнике такая схема. вот например. Объясните откуда эти числа взялись.
2 3
\ /
14 * 9
-
15 * 7
/ \
5 1
Решение: При умножении дробей мы можем сократить дроби крестом, то есть 14 и 7,15 и 9
14 мы можем сократить на семь, итого, где было 14 получится 2 (14:7), а где 7 (7:7) = 1
15 и 9, общее число, на которые мы можем их вместе поделить - это 3
15:3 = 5 (где было 15 пишем 5)
9:3=3 (где было 9 записываем 3)
Вот и все, так и сократилисокращение дробей, )
Решение: 1) обычное сокращение 4(a+1)k/a^22) b/2m^2z
3) (2b-1)/2y^2(x+y)
4) знаменатели одинаковые, значит в числителе всё суммируем, получится
9с-10y/6c+4y
5) вторую дроь сокращаем на 2 2d-3z/3d+3z
общий знаменатель (4d-z)(3d+3z)
домножаем первую на 3d+3z и вторую на 4d-z
в числителе 12d^2+12dz-12dz-12z^2-16d^2+4dz+24dz-6z^2=-4d^2+28dz-18z^2
не могу дальше понять как можно еще сократить
№1
$$ \frac{8(a+1)^2*K^2}{2a^2*(a+1)*K} = \frac{8(a-1)(a+1)*K^2}{2a^2*(a+1}*K = \frac{4(a-1)*K}{a^2} $$
№2
$$ \frac{3bz^2}{6m^2z^2} = \frac{b}{2m^2z} $$
№3
$$ \frac{6(2b-1)^2(x-y)^2}{12(2b-1)y^2(x-y)^3} = \frac{2b-1}{2y^2(x-y)} $$
№4
$$ \frac{c-5y}{6c-4y} + \frac{8c-5y}{6c-4y} = \frac{9c}{6c-4y} $$
№5
$$ \frac{4d-4z}{4d-4z} - \frac{4d-6z}{6d+6z} = \frac{-4d^2+28dz-18z^2}{(4d-z)(3d+3z)} $$Сокращение дробей \( \frac{7x^2+2x^3}{8x^2-98} \\ \frac{50x^3-8x}{10x^2+4x} \)
Решение: $$ \frac{7x^2+2x^3}{8x^2-98}= \frac{x^2(7+2x)}{2(4x^2-49)}= \frac{x^2(7+2x)}{2(2x-7)(2x+7)}= \frac{x^2}{2(2x-7)}=\frac{x^2}{4x-14} \\ \frac{50x^3-8x}{10x^2+4x}= \frac{2x(25x^2-4)}{2x(5x+2)}= \frac{(5x-2)(5x+2)}{(5x+2)}=5x-2 $$Вынесем за скобки множители в числителе и знаменателе
1)
(7x^2 + 2x^3) / (8x^2 - 98) = (x^2 * (7 + 2x)) / ( 2 * ( 4x^2 - 49)) = (x^2 * (7 + 2x)) / ( 2 * ( 2x - 7) * (2x + 7)) = (x^2) / (2 * (2x-7))
В знаменателе на третьем шаге была использована формула разложения разности квадратов
2) (50x^3-8x) / (10x^2+4x) = (2x * ( 25x^2 - 4)) / (2x * (5x+2)) = ( 2x * (5x-2) * (5x+2)) / ( 2x*(5x+2)) = 5x-2
В числителе на третьем шаге была использована формула разложения разности квадратовСокращение дробей: 1) \( \frac{2a^5 - 128a^2}{(2a^2+8a+32)(a^4 -4a^3)} \); 2) \( \frac{2a^4+3a^3+2a+3}{(a^2-a+1)(2a+3)} \)
Решение: Первая дробь в числителе выносим за скобку 2a^ получаем разность кубов, расписываем. В знаменателе выносим 2 и a^3=
=2a^(a-4)(a^+4a+16) / 2(a^+4a+16)a^3(a-4) сокращаем = 1/a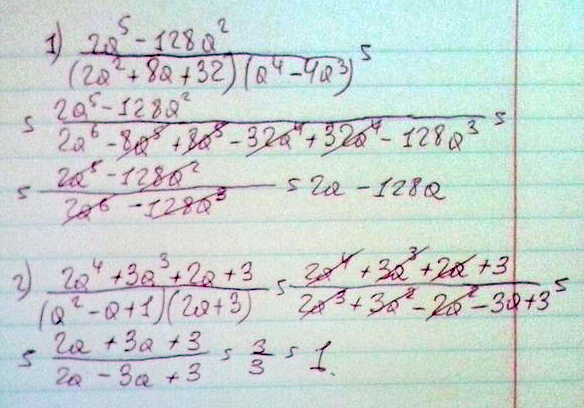
Что такое сокращение дробей?
Решение: Сократить дробь – это значит разделить ее числитель и знаменатель на их положительный и отличный от единицы общий делитель. Понятно, что в результате сокращения дроби получается новая дробь с меньшим числителем и знаменателем, причем, в силу основного свойства дроби, полученная дробь равна исходной. Для примера, проведем сокращение обыкновенной дроби 8/24, разделив ее числитель и знаменатель на 2. Иными словами, сократим дробь 8/24 на 2. Так как8:2=4 и 24:2=12, то в результате такого сокращения получается дробь 4/12, которая равна исходной дроби 8/24 (смотрите равные и неравные дроби). В итоге имеем.

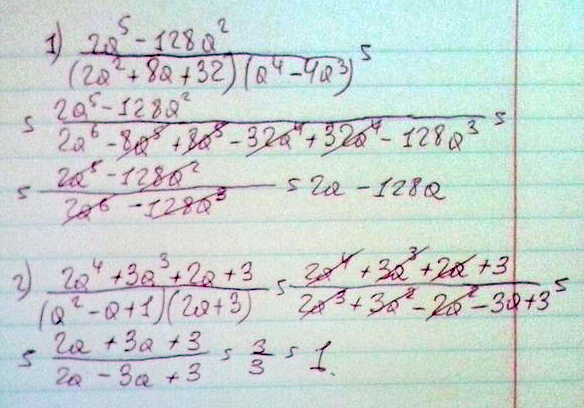
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...